P1313 [NOIP2011 提高组] 计算系数——二项式定理

[NOIP2011 提高组] 计算系数

题目描述

给定一个多项式 $(by+ax{)}^k$，请求出多项式展开后 $x^n\times y^m$ 项的系数。

输入格式

输入共一行，包含 $5$ 个整数，分别为 $a,b,k,n,m$，每两个整数之间用一个空格隔开。

输出格式

输出共一行，包含一个整数，表示所求的系数。

这个系数可能很大，输出对 $10007$ 取模后的结果。

样例 #1

样例输入 #1

1 1 3 1 2

样例输出 #1

3

提示

【数据范围】

对于 $30\%$ 的数据，有 $0\le k\le 10$。

对于 $50\%$ 的数据，有 $a=1$，$b=1$。

对于 $100\%$ 的数据，有 $0\le k\le 1000$，$0\le n,m\le k$，$n+m=k$，$0\le a,b\le 10^6$。

noip2011 提高组 day2 第 1 题。

思路

读到 $(by+ax{)}^k$ 这句话是，不知道各位有没有一种莫名的$“亲切感”$，没错，他就是著名的二项式定理。那到底什么是二项式定理呢？

我们都知道，$(a+b{)}^2$ = $a^2$+ $b^2$ + $2ab$ 可这个公式是怎么得来的呢？这就要说到 二项式定理 了，在说二项式定理之前，我们先要了解一下 排列组合：

排列组合

排列：

我们通常用 $A_n^m$ 来表示排列，表示从$n$个物体中 有顺序的选取$m$个（也就是选取第1、2、3个和选取第2、1、3个属于两种情况），此外规定 0！= 1，计算公式如下：

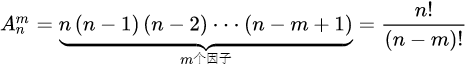
组合：

我们用 $C_n^m$ 来表示组合，表示从$n$个物体中 无顺序的选取$m$个 （也就是选取第1、2、3个和选取第2、1、3个属于同一种情况），此外规定 0！= 1，计算公式如下：

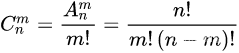
初步了解排列组合之后，我们回归正传，来看二项式定理：

二项式定理

二项式定理，又称牛顿二项式定理，由艾萨克·牛顿于1664年、1665年间提出。该定理给出两个数之和的整数次幂诸如展开为类似项之和的恒等
式。二项式定理可以推广到任意实数次幂，即广义二项式定理 。

看这段话的话可能有些难以理解，总体来讲，就是用来求 $(x+y{)}^n$ 的公式：

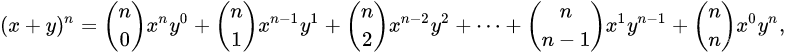
其中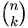，表示即 $C_k^n$。
也可把它写成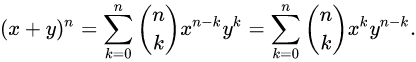

举个例子：

$(2+3{)}^3$ = $C_3^0$ $\times$ $2^3$ $\times$ $3^0$ + $C_3^1$ $\times$ $2^2$ $\times$ $3^1$ + $C_3^2$ $\times$ $2^1$ $\times$ $3^2$ + $C_3^3$ $\times$ $2^0$ $\times$ $3^3$
= $1\times 8\times 1$ + $3\times 4\times 3$ + $3\times 2\times 9$ + $1\times 1\times 27$
= $8+36+54+27$
= 125

解题方法

由于题目希望求出多项式$(by+ax{)}^k$，展开后的多项式$x^n\times y^n$的系数，我们可以通过 二项式定理来进行推导：

设$A$ = $by$，$B$ = $ax$，$m$ = $k-n$
通过二项式定理并由 $(by+ax{)}^k$ 得
$(by+ax{)}^k$ = $C_k^0\times A^k\times B^0$ + $C_k^1\times A^{k-1}\times B^1$ + …… + $C_k^n\times A^m\times B^n$ + …… + $C_k^k\times A^0\times B^k$
= $C_k^0\times b^k{y}^k\times a^0{x}^0$ + $C_k^1\times b^{k-1}{y}^{k-1}\times a^1{x}^1$ + …… + $C_k^n\times b^m{y}^m\times a^n{x}^n$ + …… + $C_k^k\times b^0{y}^0\times a^k{x}^k$
= $C_k^0\times a^0\times b^k$ $\times x^0\times y^k$ + …… + $C_k^n\times a^n\times b^m$ $\times x^n\times y^m$ + …… + $C_k^0\times a^k\times b^0$ $\times x^k\times y^0$

得标黄的部分为多项式的系数

#include <bits/stdc++.h>
using namespace std;
const int M = 10007;
long long c[1005][1005];
long long pow(long long x, long long y){//快速幂，快速求出x^y 
	if(y == 0){
		return 1;
	}
	long long tmp = pow(x, y / 2) % M;
	if(y % 2 == 0){
		return tmp%M * tmp%M;
	} else {
		return tmp * tmp % M * x;
	}
}
int main(){
	long long a, b, k, n, m;
	cin >> a >> b >> k >> n >> m;
	c[0][0] = c[1][0] = c[1][1] = 1;
	for(int i = 2; i <= k; i++){
		for(int j = 0; j <= i; j++){
			if(j == 0){
				c[i][j] = 1;
			} else {
				c[i][j] = (c[i-1][j] + c[i-1][j-1]) % M;
			}
		}
	}
	cout << c[k][n] * pow(a, n) % M * pow(b, m) % M;	 
	return 0;
}