《动手学深度学习》笔记——预备知识(数据操作、数据预处理、线性代数、梯度、自动微分、概率)
PyTorch张量的各种语法可大致参考NumPy数组
深度学习基础笔记 (1) :预备知识(张量、梯度、概率…)
深度学习基础笔记 (2) :深度神经网络 DNN
深度学习基础笔记 (3) :优化算法(梯度下降、冲量法、Adam…)
深度学习基础笔记 (4) :卷积神经网络 CNN
深度学习基础笔记 (5) :计算机视觉(目标检测、语义分割、样式迁移)
深度学习基础笔记 (6) :注意力机制、Transformer
深度学习PyTorch代码模板
文章目录
1 数据操作
1.1 n维数组与张量
n n n维数组 / n n n阶张量是机器学习和神经网络的主要数据结构
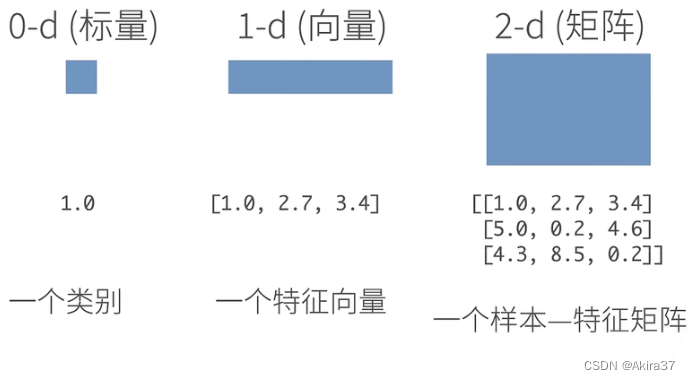
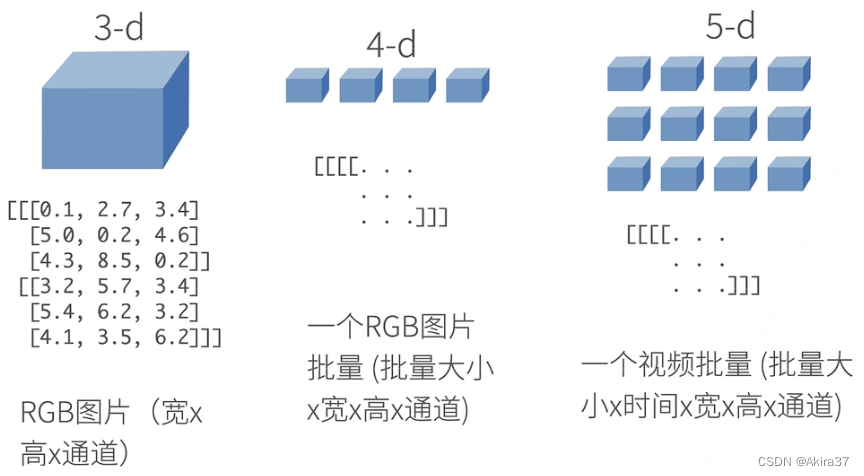
1.2 初始化
x = torch.arange(10) # tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x = torch.zeros((2, 3, 4)) # 全0
x = torch.ones((2, 3, 4)) # 全1
x = torch.randn(3, 4) # 均值为0、标准差为1的标准正态分布
x = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]]) # 根据(嵌套)列表为每个元素赋确定值
# 查看形状
x.shape # 返回形状类:torch.Size(维度张量)
x.shape[0] # 获取维度张量
# 获取元素个数
x.numel() # 计算张量中元素的总数(维度的乘积)
# 变形
X = x.reshape(3, -1) # 用-1自动计算维度
1.3 访问元素
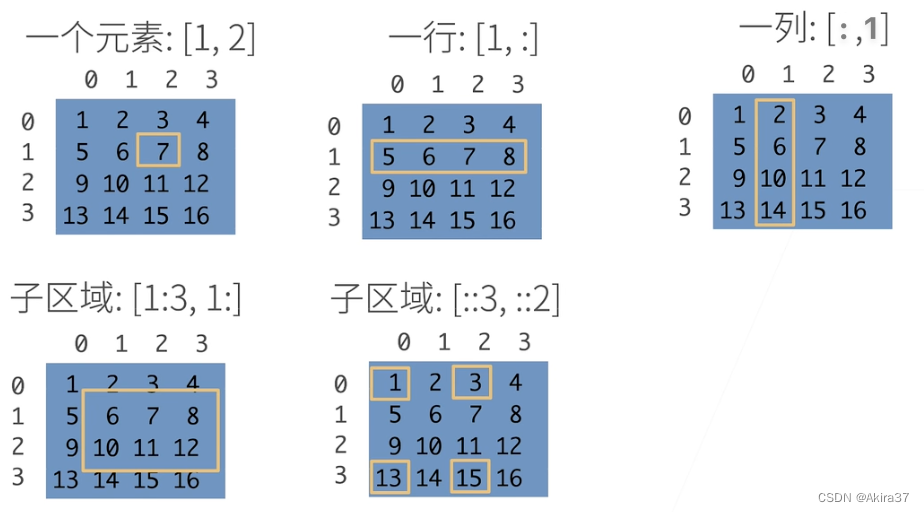
X[-1] # 选择最后一个元素
X[1:3] # 选择索引在[1, 3)上的元素(左开右闭,右-左 为切片长度,下同)
X[1, 2] = 9 # 指定索引写入元素
X[0:2, :] = 12 # 在索引0~1行批量写入元素
1.4 运算
# 按元素运算
X + Y, X - Y, X * Y, X / Y, X ** Y # 所有基本运算符均升级为按元素运算(形状不同则广播,下同)
torch.exp(X) # 指数运算
X == Y # 通过逻辑运算符构建二元张量(True / False)
# 连结(dim=x: 沿轴x……)
torch.cat((X, Y), dim=0) # 沿轴0(行)连结张量(上下拼接)
torch.cat((X, Y), dim=1) # 沿轴1(列)连结张量(左右拼接)
# 降维函数(详见下文)
X.sum() # 求和(返回只含1个元素的张量,下同)
X.mean() # 求平均值
# 与NumPy数组的转换
A = X.numpy() # 张量转化为n维数组(numpy.ndarray)
B = torch.tensor(A) # n维数组转化为张量(torch.Tensor)
# 与Python标量的转换
a = torch.tensor([3.7]) # 大小为1的张量 tensor([3.7000])
a.item() # 调用方法获取元素
float(a), int(a) # 使用python
2 数据预处理
2.1 创建人工数据集
创建一个人工数据集,存储于csv(逗号分割值)文件中
import os
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms, Alley, Price\n') # 列名
f.write('NA, Pave, 127500\n') # 每行表示一个数据样本
f.write('2, NA, 106000\n')
f.write('4, NA, 178100\n')
f.write('NA, NA, 140000\n')
2.2 读取数据集
从创建的csv文件中加载原始数据集
import pandas as pd
data = pd.read_csv(data_file) # pandas读取csv文件
print(data)
2.3 处理缺失数据
# 使用插值法
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean()) # 填充缺失值为均值(仅适用于数值类型数据)
inputs = pd.get_dummies(inputs, dummy_na=True) # 视为特征:缺失值 - Alley_nan,Str - Alley
# 所有条目都是数值类型,故可转换成张量
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
3 线性代数
3.1 标量
- 按元素操作 c = a + b c = a ⋅ b c = sin a c=a+b \\ c=a\cdot b \\ c=\sin a c=a+bc=a⋅bc=sina
- 长度 ∣ a ∣ = { a if a > 0 − a otherwise ∣ a + b ∣ ≤ ∣ a ∣ + ∣ b ∣ ∣ a ⋅ b ∣ = ∣ a ∣ ⋅ ∣ b ∣ |a|=\begin{cases} a & \text{ if } a>0 \\ -a & \text{ otherwise } \end{cases} \\ |a+b|≤|a|+|b| \\ |a \cdot b|=|a| \cdot |b| ∣a∣={a−a if a>0 otherwise ∣a+b∣≤∣a∣+∣b∣∣a⋅b∣=∣a∣⋅∣b∣
3.2 向量
- 按元素操作
c
=
a
+
b
where
c
i
=
a
i
+
b
i
c
=
a
⋅
b
where
c
i
=
a
⋅
b
i
c
=
sin
a
where
c
i
=
sin
a
i
\begin{align*} \mathbf{c}=\mathbf{a}+\mathbf{b}& \text{ where } c_i=a_i+b_i \\ \mathbf{c}=a \cdot \mathbf{b} & \text{ where } c_i=a\cdot b_i \\ \mathbf{c}=\sin \mathbf{a} & \text{ where } c_i=\sin a_i \end{align*}
c=a+bc=a⋅bc=sina where ci=ai+bi where ci=a⋅bi where ci=sinai

- 长度( L 2 L_2 L2范数) ∥ a ∥ 2 = [ ∑ i = 1 m a i 2 ] 1 2 ∥ a ∥ ≥ 0 for all a ∥ a ⋅ b ∥ = ∣ a ∣ ⋅ ∥ b ∥ \left\| \mathbf{a}\right\|_2=[\sum_{i=1}^m a_i^2]^{\frac12}\\ \left\| \mathbf{a}\right\|≥0 \text{ for all }\mathbf{a}\\ \left\| a \cdot \mathbf{b} \right\|=|a| \cdot \left\| \mathbf{b}\right\| ∥a∥2=[i=1∑mai2]21∥a∥≥0 for all a∥a⋅b∥=∣a∣⋅∥b∥
- 点积 ⟨ a , b ⟩ = a T b = ∑ i a i b i ⟨ a , b ⟩ = a T b = 0 ⇔ a ⊥ b \left \langle \mathbf{a},\mathbf{b} \right \rangle =\mathbf{a}^{\text{T}}\mathbf{b}=\sum_i a_ib_i \\ \left \langle \mathbf{a},\mathbf{b} \right \rangle =\mathbf{a}^{\text{T}}\mathbf{b}=0 \Leftrightarrow \mathbf{a}\ \bot\ \mathbf{b} ⟨a,b⟩=aTb=i∑aibi⟨a,b⟩=aTb=0⇔a ⊥ b
3.3 矩阵
- 按元素操作 C = A + B where C i j = A i j + B i j C = a B where C i j = a B i j C = sin A where C i j = sin A i j \begin{align*} \mathbf{C}=\mathbf{A}+\mathbf{B}& \text{ where } C_{ij}=A_{ij}+B_{ij} \\ \mathbf{C}=a \mathbf{B} & \text{ where } C_{ij}=a B_{ij} \\ \mathbf{C}=\sin \mathbf{A} & \text{ where } C_{ij}=\sin A_{ij} \end{align*} C=A+BC=aBC=sinA where Cij=Aij+Bij where Cij=aBij where Cij=sinAij
- 矩阵向量积
c
=
A
b
where
c
i
=
∑
j
A
i
j
b
j
\mathbf{c}=\mathbf{Ab} \text{ where } c_i=\sum_j A_{ij}b_j
c=Ab where ci=j∑Aijbj

- 矩阵乘法 C = A B where C i k = ∑ j A i j B j k \mathbf{C}=\mathbf{AB} \text{ where } C_{ik}=\sum_j A_{ij}B_{jk} C=AB where Cik=j∑AijBjk
- 范数
- 矩阵范数:满足 c = A b hence ∥ c ∥ ≤ ∥ A ∥ ⋅ ∥ b ∥ \mathbf{c}=\mathbf{Ab} \text{ hence } \left\| \mathbf{c}\right\|≤\left\|\mathbf{A}\right\|\cdot\left\| \mathbf{b}\right\| c=Ab hence ∥c∥≤∥A∥⋅∥b∥ 的最小值
- Frobenius范数(更常用) ∥ A ∥ Frob = [ ∑ i j A i j 2 ] 1 2 \left\| \mathbf{A}\right\|_{\text{Frob}}=[\sum\limits_{ij}A_{ij}^2]^{\frac12} ∥A∥Frob=[ij∑Aij2]21
- 特殊矩阵
- 对称矩阵、反对称矩阵: A i j = A j i \mathbf{A}_{ij}=\mathbf{A}_{ji} Aij=Aji 、 A i j = − A j i \mathbf{A}_{ij}=-\mathbf{A}_{ji} Aij=−Aji
- 正定矩阵: ∥ x ∥ 2 = x T x ≥ 0 generalizes to x T A x ≥ 0 \left\| \mathbf{x}\right\|^2=\mathbf{x}^{\text{T}}\mathbf{x}≥0 \text{ generalizes to } \mathbf{x}^{\text{T}}\mathbf{Ax}≥0 ∥x∥2=xTx≥0 generalizes to xTAx≥0
- 正交矩阵:QQ^T=1
- 置换矩阵: P where P i j = 1 if and only if j = π ( i ) \mathbf{P} \text{ where } P_{ij}=1 \text{ if and only if } j=\pi(i) P where Pij=1 if and only if j=π(i) 。置换矩阵必正交。
- 特征向量和特征值:
A
x
=
λ
x
\mathbf{Ax}=\lambda \mathbf{x}
Ax=λx
- 特征向量:不被矩阵改变方向的向量
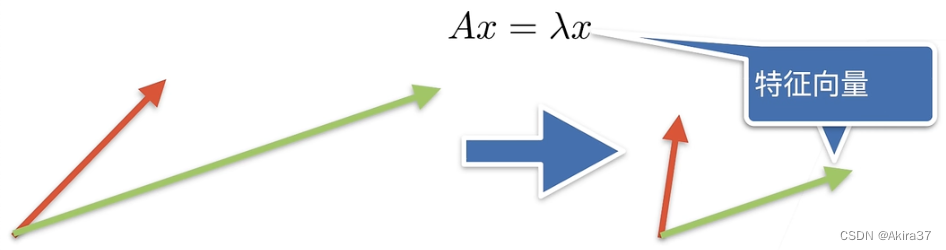
- 特征向量:不被矩阵改变方向的向量
3.4 PyTorch实现
a = torch.tensor([3.0])
x = torch.arange(10, dtype=torch.float32)
A = torch.arange(20, dtype=torch.float32).reshape(5, 4) # 5x4的矩阵
len(x)
A.shape
# 转置
A.T
# 深拷贝
B = A.clone()
# 按元素操作
A + B
A * B # 哈达玛积
# 求和
A.sum() # 对所有元素求和,降为标量
A.sum(axis=0) # 沿轴0(行)求和,降为向量(参考连结方法cat())
A.sum(axis=[0, 1]) # 沿轴0、轴1求和,同方法sum()
# 求平均值
A.mean() # 等价于 A.sum() / A.numel()
A.mean(axis=0) # 等价于 A.sum(axis=0) / A.shape[0]
# 保持轴数不变,便于广播
sum_A = A.sum(axis=1, keepdims=True) # 对每一行求和
A / sum_A # 每个元素分别除以其所在行元素和
# 累加求和
A.cumsum(axis=0) # 沿轴0累加求和(形状不变)
# 向量点积(PyTorch的点积只能计算向量!)
torch.dot(x, y) # 等价于torch.sum(x * y)
# 矩阵向量积
torch.mv(A, x)
# 矩阵乘法
torch.mm(A, A)
# L2范数:向量元素的平方和的平方根
torch.norm(x)
# L1范数:向量元素的绝对值之和
torch.abs(x).sum()
# Frobenius范数:矩阵元素的平方和的平方根
torch.norm(A)
4 梯度
梯度是一个向量,指向函数变化率最大的方向。
标量 向量 矩阵 x ( 1 , ) x ( n , 1 ) X ( n , k ) 标量 y ( 1 , ) ∂ y ∂ x ( 1 , ) ∂ y ∂ x ( 1 , n ) ∂ y ∂ X ( k , n ) 向量 y ( m , 1 ) ∂ y ∂ x ( m , 1 ) ∂ y ∂ x ( m , n ) ∂ y ∂ X ( m , k , n ) 矩阵 Y ( m , l ) ∂ Y ∂ x ( m , l ) ∂ Y ∂ x ( m , l , n ) ∂ Y ∂ X ( m , l , k , n ) \begin{matrix} & & 标量 & 向量 & 矩阵\\ & &\underset{(1,)}{x} & \underset{(n,1)}{\mathbf{x}} & \underset{(n,k)}{\mathbf{X}}\\ 标量 & \underset{(1,)}{y} & \underset{(1,)}{\frac{\partial y}{\partial x}} & \underset{(1,n)}{\frac{\partial y}{\partial \mathbf{x} }} & \underset{(k,n)}{\frac{\partial y}{\partial \mathbf{X}}} \\ 向量 & \underset{(m,1)}{\mathbf{y}} & \underset{(m,1)}{\frac{\partial \mathbf{y} }{\partial x}} & \underset{(m,n)}{\frac{\partial \mathbf{y} }{\partial \mathbf{x} }} & \underset{(m,k,n)}{\frac{\partial \mathbf{y}}{\partial \mathbf{X}}} \\ 矩阵 & \underset{(m,l)}{\mathbf{Y}} & \underset{(m,l)}{\frac{\partial \mathbf{Y}}{\partial x}} & \underset{(m,l,n)}{\frac{\partial \mathbf{Y}}{\partial \mathbf{x}}} & \underset{(m,l,k,n)}{\frac{\partial \mathbf{Y}}{\partial \mathbf{X}}} \end{matrix} 标量向量矩阵(1,)y(m,1)y(m,l)Y标量(1,)x(1,)∂x∂y(m,1)∂x∂y(m,l)∂x∂Y向量(n,1)x(1,n)∂x∂y(m,n)∂x∂y(m,l,n)∂x∂Y矩阵(n,k)X(k,n)∂X∂y(m,k,n)∂X∂y(m,l,k,n)∂X∂Y
4.1 标量导数
对于单变量函数,梯度即为导数
| y y y | a a a | x n x^n xn | exp ( x ) \exp(x) exp(x) | log ( x ) \log(x) log(x) | sin ( x ) \sin(x) sin(x) |
|---|---|---|---|---|---|
| d y d x \frac{\mathrm{d} y}{\mathrm{d} x} dxdy | 0 0 0 | n x n − 1 nx^{n-1} nxn−1 | exp ( x ) \exp(x) exp(x) | 1 x \frac1x x1 | cos ( x ) \cos(x) cos(x) |
| y y y | u + v u+v u+v | u v uv uv | y = f ( u ) , u = g ( x ) y=f(u),u=g(x) y=f(u),u=g(x) |
|---|---|---|---|
| d y d x \frac{\mathrm{d} y}{\mathrm{d} x} dxdy | d u d x + d v d x \frac{\mathrm{d} u}{\mathrm{d} x}+\frac{\mathrm{d} v}{\mathrm{d} x} dxdu+dxdv | d u d x v + d v d x u \frac{\mathrm{d} u}{\mathrm{d} x}v+\frac{\mathrm{d} v}{\mathrm{d} x}u dxduv+dxdvu | d y d u d u d x \frac{\mathrm{d} y}{\mathrm{d} u}\frac{\mathrm{d} u}{\mathrm{d} x} dudydxdu |
4.2 标量对向量求导
标量
y
y
y 对向量
x
\mathbf{x}
x 的每一个分量求导,组成行向量
x
=
[
x
1
x
2
⋮
x
n
]
,
∂
y
∂
x
=
[
∂
y
∂
x
1
,
∂
y
∂
x
2
,
⋯
,
∂
y
∂
x
n
]
\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix},\ \frac{\partial y}{\partial \mathbf{x} } =[ \frac{\partial y}{\partial x_1} , \frac{\partial y}{\partial x_2} ,\cdots, \frac{\partial y}{\partial x_n}]
x=
x1x2⋮xn
, ∂x∂y=[∂x1∂y,∂x2∂y,⋯,∂xn∂y]
| y y y | a a a | a u au au | sum ( x ) \text{sum}(\mathbf{x}) sum(x) | ∥ x ∥ 2 \lVert \mathbf{x} \rVert^2 ∥x∥2 |
|---|---|---|---|---|
| ∂ y ∂ x \frac{\partial y}{\partial \mathbf{x} } ∂x∂y | 0 T \mathbf{0}^{\text{T}} 0T | a ∂ u ∂ x a\frac{\partial u}{\partial \mathbf{x} } a∂x∂u | 1 T \mathbf{1}^{\text{T}} 1T | 2 x T 2\mathbf{x}^{\text{T}} 2xT |
| y y y | u + v u+v u+v | u v uv uv | ⟨ u , v ⟩ = u T v \left \langle \mathbf{u} ,\mathbf{v} \right \rangle=\mathbf{u}^{\text{T}}\mathbf{v} ⟨u,v⟩=uTv |
|---|---|---|---|
| ∂ y ∂ x \frac{\partial y}{\partial \mathbf{x} } ∂x∂y | ∂ u ∂ x + ∂ v ∂ x \frac{\partial u}{\partial \mathbf{x}}+\frac{\partial v}{\partial \mathbf{x}} ∂x∂u+∂x∂v | ∂ u ∂ x v + ∂ v ∂ x u \frac{\partial u}{\partial \mathbf{x}}v+\frac{\partial v}{\partial \mathbf{x}}u ∂x∂uv+∂x∂vu | u T ∂ v ∂ x + v T ∂ u ∂ x \mathbf{u}^{\text{T}}\frac{\partial \mathbf{v}}{\partial \mathbf{x}}+\mathbf{v}^{\text{T}}\frac{\partial \mathbf{u}}{\partial \mathbf{x}} uT∂x∂v+vT∂x∂u |
4.3 向量对标量求导
向量
y
\mathbf{y}
y 的每一个分量对标量
x
x
x 求导,组成列向量
y
=
[
y
1
y
2
⋮
y
m
]
,
∂
y
∂
x
=
[
∂
y
1
∂
x
∂
y
1
∂
x
⋮
∂
y
m
∂
x
]
\mathbf{y}=\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix},\ \frac{\partial \mathbf{y}}{\partial x} =\begin{bmatrix} \frac{\partial y_1}{\partial x} \\ \frac{\partial y_1}{\partial x} \\ \vdots \\ \frac{\partial y_m}{\partial x} \end{bmatrix}
y=
y1y2⋮ym
, ∂x∂y=
∂x∂y1∂x∂y1⋮∂x∂ym
4.4 向量对向量求导
向量 y \mathbf{y} y 的每一个分量对向量 x \mathbf{x} x 的每一个分量求导,先展开 y \mathbf{y} y 再展开 x \mathbf{x} x 可得,结果为矩阵
x = [ x 1 x 2 ⋮ x n ] , y = [ y 1 y 2 ⋮ y m ] , ∂ y ∂ x = [ ∂ y 1 ∂ x ∂ y 2 ∂ x ⋮ ∂ y m ∂ x ] = [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ⋯ ∂ y 1 ∂ x n ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ⋯ ∂ y 2 ∂ x n ⋮ ⋮ ⋮ ∂ y m ∂ x 1 ∂ y m ∂ x 2 ⋯ ∂ y m ∂ x n ] \mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix},\ \mathbf{y}=\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix},\ \frac{\partial \mathbf{y} }{\partial \mathbf{x} }=\begin{bmatrix} \frac{\partial y_1}{\partial \mathbf{x} } \\ \frac{\partial y_2}{\partial \mathbf{x} } \\ \vdots \\ \frac{\partial y_m}{\partial \mathbf{x} } \end{bmatrix} =\begin{bmatrix} \frac{\partial y_1}{\partial x_1}&\frac{\partial y_1}{\partial x_2}&\cdots&\frac{\partial y_1}{\partial x_n} \\ \frac{\partial y_2}{\partial x_1}&\frac{\partial y_2}{\partial x_2}&\cdots&\frac{\partial y_2}{\partial x_n} \\ \vdots&\vdots&&\vdots \\ \frac{\partial y_m}{\partial x_1}&\frac{\partial y_m}{\partial x_2}&\cdots&\frac{\partial y_m}{\partial x_n} \end{bmatrix} x= x1x2⋮xn , y= y1y2⋮ym , ∂x∂y= ∂x∂y1∂x∂y2⋮∂x∂ym = ∂x1∂y1∂x1∂y2⋮∂x1∂ym∂x2∂y1∂x2∂y2⋮∂x2∂ym⋯⋯⋯∂xn∂y1∂xn∂y2⋮∂xn∂ym
| y \mathbf{y} y | a \mathbf{a} a | x \mathbf{x} x | A x \mathbf{Ax} Ax | x T A \mathbf{x}^{\text{T}}\mathbf{A} xTA |
|---|---|---|---|---|
| ∂ y ∂ x \frac{\partial \mathbf{y} }{\partial \mathbf{x} } ∂x∂y | 0 \mathbf{0} 0 | I \mathbf{I} I | A \mathbf{A} A | A T \mathbf{A}^{\text{T}} AT |
| y \mathbf{y} y | a u a\mathbf{u} au | A u \mathbf{Au} Au | u + v \mathbf{u}+\mathbf{v} u+v |
|---|---|---|---|
| ∂ y ∂ x \frac{\partial \mathbf{y} }{\partial \mathbf{x} } ∂x∂y | a ∂ u ∂ x a\frac{\partial \mathbf{u} }{\partial \mathbf{x} } a∂x∂u | A ∂ u ∂ x \mathbf{A}\frac{\partial \mathbf{u} }{\partial \mathbf{x} } A∂x∂u | ∂ u ∂ x + ∂ v ∂ x \frac{\partial \mathbf{u} }{\partial \mathbf{x} }+\frac{\partial \mathbf{v} }{\partial \mathbf{x} } ∂x∂u+∂x∂v |
5 自动微分
5.1 向量链式法则
将标量链式法则拓展到向量,可得
∂ y ∂ x ( 1 , n ) = ∂ y ∂ u ( 1 , ) ∂ u ∂ x ( 1 , n ) , ∂ y ∂ x ( 1 , n ) = ∂ y ∂ u ( 1 , k ) ∂ u ∂ x ( k , n ) , ∂ y ∂ x ( m , n ) = ∂ y ∂ u ( m , k ) ∂ u ∂ x ( k , n ) \underset{(1,n)}{\frac{\partial y}{\partial \mathbf{x}}}=\underset{(1,)}{\frac{\partial y}{\partial u}}\underset{(1,n)}{\frac{\partial u}{\partial \mathbf{x} }},\ \underset{(1,n)}{\frac{\partial y}{\partial \mathbf{x} }}=\underset{(1,k)}{\frac{\partial y}{\partial \mathbf{u} }}\underset{(k,n)}{\frac{\partial \mathbf{u} }{\partial \mathbf{x} }},\ \underset{(m,n)}{\frac{\partial \mathbf{y} }{\partial \mathbf{x} }}=\underset{(m,k)}{\frac{\partial \mathbf{y} }{\partial \mathbf{u} }}\underset{(k,n)}{\frac{\partial \mathbf{u} }{\partial \mathbf{x}}} (1,n)∂x∂y=(1,)∂u∂y(1,n)∂x∂u, (1,n)∂x∂y=(1,k)∂u∂y(k,n)∂x∂u, (m,n)∂x∂y=(m,k)∂u∂y(k,n)∂x∂u
【例1】设
x
,
w
∈
R
n
,
y
∈
R
,
z
=
(
⟨
x
,
w
⟩
−
y
)
2
\mathbf{x},\mathbf{w} \in \mathbb{R}^n,\ y\in \mathbb{R},\ z=(\left \langle \mathbf{x},\mathbf{w} \right \rangle -y )^2
x,w∈Rn, y∈R, z=(⟨x,w⟩−y)2 ,求
∂
z
∂
w
\frac{\partial z}{\partial \mathbf{w} }
∂w∂z
【解】令
a
=
⟨
x
,
w
⟩
,
b
=
a
−
y
,
z
=
b
2
a=\left \langle \mathbf{x},\mathbf{w} \right \rangle,\ b=a-y,\ z=b^2
a=⟨x,w⟩, b=a−y, z=b2 ,则
∂
z
∂
w
=
∂
z
∂
b
∂
b
∂
a
∂
a
∂
w
=
∂
b
2
∂
b
∂
a
−
y
∂
a
∂
⟨
x
,
w
⟩
∂
w
=
2
b
⋅
1
⋅
x
T
=
2
(
⟨
x
,
w
⟩
−
y
)
x
T
\begin{align*} \frac{\partial z}{\partial \mathbf{w} } = & \frac{\partial z}{\partial b} \frac{\partial b}{\partial a} \frac{\partial a}{\partial \mathbf{w} } \\ = & \frac{\partial b^2}{\partial b}\frac{\partial a-y}{\partial a}\frac{\partial \left \langle \mathbf{x},\mathbf{w} \right \rangle}{\partial \mathbf{w}}\\ = & 2b \cdot1\cdot \mathbf{x}^{\text{T}} \\ = & 2(\left \langle \mathbf{x},\mathbf{w} \right \rangle -y) \mathbf{x}^{\text{T}} \end{align*}
∂w∂z====∂b∂z∂a∂b∂w∂a∂b∂b2∂a∂a−y∂w∂⟨x,w⟩2b⋅1⋅xT2(⟨x,w⟩−y)xT
【例2】设
X
∈
R
m
×
n
,
w
∈
R
n
,
y
∈
R
m
,
z
=
∥
X
w
−
y
∥
2
\mathbf{X} \in \mathbb{R}^{m\times n},\ \mathbf{w} \in \mathbb{R}^n,\ \mathbf{y}\in \mathbb{R}^m,\ z=\lVert\mathbf{Xw}-\mathbf{y} \rVert^2
X∈Rm×n, w∈Rn, y∈Rm, z=∥Xw−y∥2 ,求
∂
z
∂
w
\frac{\partial z}{\partial \mathbf{w} }
∂w∂z
【解】令
a
=
X
w
,
b
=
a
−
y
,
z
=
∥
b
∥
2
\mathbf{a}=\mathbf{Xw},\ \mathbf{b}=\mathbf{a}-\mathbf{y},\ z=\lVert \mathbf{b} \rVert^2
a=Xw, b=a−y, z=∥b∥2 ,则
∂
z
∂
w
=
∂
z
∂
b
∂
b
∂
a
∂
a
∂
w
=
∂
∥
b
∥
2
∂
b
∂
a
−
y
∂
a
∂
X
w
∂
w
=
2
b
T
×
I
×
X
=
2
(
X
w
−
y
)
T
X
\begin{align*} \frac{\partial z}{\partial \mathbf{w} } = & \frac{\partial z}{\partial \mathbf{b} } \frac{\partial \mathbf{b} }{\partial \mathbf{a} } \frac{\partial \mathbf{a} }{\partial \mathbf{w} } \\ = & \frac{\partial \lVert\mathbf{b}\rVert ^2}{\partial \mathbf{b} }\frac{\partial \mathbf{a}-\mathbf{y}}{\partial \mathbf{a} }\frac{\partial \mathbf{Xw} }{\partial \mathbf{w}}\\ = & 2\mathbf{b}^{\text{T}} \times\mathbf{I} \times \mathbf{X} \\ = & 2(\mathbf{Xw} -\mathbf{y} )^{\text{T}}\mathbf{X} \end{align*}
∂w∂z====∂b∂z∂a∂b∂w∂a∂b∂∥b∥2∂a∂a−y∂w∂Xw2bT×I×X2(Xw−y)TX
5.2 自动求导
自动求导计算一个函数在指定值上的导数:1. 将代码分解成操作子;2. 将计算表示成一个无环图(计算图)
- 符号求导 D x [ 4 x 3 + x 2 + 3 ] = 12 x 2 + 2 x D_x[4x^3 + x^2 + 3]=12x^2 +2x Dx[4x3+x2+3]=12x2+2x
- 数值求导 ∂ f ( x ) ∂ x = lim h → 0 f ( x + h ) − f ( x ) h \frac{\partial f(x)}{\partial x} =\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} ∂x∂f(x)=h→0limhf(x+h)−f(x)
由链式法则 ∂ y ∂ x = ∂ y ∂ u n ∂ u n ∂ u n − 1 ⋯ ∂ u 2 ∂ u 1 ∂ u 1 ∂ x \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}\frac{\partial u_n}{\partial u_{n-1}}\cdots\frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x} ∂x∂y=∂un∂y∂un−1∂un⋯∂u1∂u2∂x∂u1 可得自动求导的两种模式:
- 正向累积(时间复杂度太高,不常用): ∂ y ∂ x = ∂ y ∂ u n ( ∂ u n ∂ u n − 1 ( ⋯ ( ∂ u 2 ∂ u 1 ∂ u 1 ∂ x ) ) ) \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}(\frac{\partial u_n}{\partial u_{n-1}}(\cdots(\frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x}))) ∂x∂y=∂un∂y(∂un−1∂un(⋯(∂u1∂u2∂x∂u1)))
- 反向累积(反向传递,如下图所示):
∂
y
∂
x
=
(
(
(
∂
y
∂
u
n
∂
u
n
∂
u
n
−
1
)
⋯
)
∂
u
2
∂
u
1
)
∂
u
1
∂
x
\frac{\partial y}{\partial x}=(((\frac{\partial y}{\partial u_n}\frac{\partial u_n}{\partial u_{n-1}})\cdots)\frac{\partial u_2}{\partial u_1})\frac{\partial u_1}{\partial x}
∂x∂y=(((∂un∂y∂un−1∂un)⋯)∂u1∂u2)∂x∂u1

- 反向传递的过程
- 构造计算图
- 前向:执行图,存储中间结果
- 反向:从相反方向执行图(同时去除不需要的枝)
5.3 PyTorch实现
【例1】设函数 y = 2 x T x y=2\mathbf{x}^{\text{T}}\mathbf{x} y=2xTx ,通过自动求导求 ∂ y ∂ x \frac{\partial y}{\partial \mathbf{x} } ∂x∂y
import torch
# x = torch.arange(4.0) # tensor([0., 1., 2., 3.])
x = torch.arange(4.0, requires_grad=True) # 开启梯度存储,用x.grad获取梯度
y = 2 * torch.dot(x, x) # tensor(28., grad_fn=<MulBackward0>)
y.backward() # 调用反向传播函数来自动计算标量y关于向量x每个分量的梯度
x.grad # (tensor([0., 4., 8., 12.])
【例2】设函数 y = sum ( x ) y=\text{sum}(\mathbf{x}) y=sum(x) ,通过自动求导求 ∂ y ∂ x \frac{\partial y}{\partial \mathbf{x} } ∂x∂y
x.grad.zero_() # PyTorch默认累积梯度,故需清除之前的梯度(以单下划线结尾的函数表示重写内容)
y = x.sum()
y.backward()
x.grad # tensor([1., 1., 1., 1.])
【例3】设函数
y
=
x
⊙
x
\mathbf{y}=\mathbf{x}\odot \mathbf{x}
y=x⊙x ,通过自动求导求
∂
y
∂
x
\frac{\partial \mathbf{y}}{\partial \mathbf{x} }
∂x∂y
深度学习中,我们的目的不是计算微分矩阵,而是批量中每个样本单独计算的偏导数之和。
对非标量调用
backward()需要传入一个gradient参数,该参数指定微分函数关于self的梯度
本例只想求偏导数的和,所以应传入分量全为 1 1 1 的梯度(由求导公式 ∂ sum ( x ) ∂ x = 1 T \frac{\partial \text{sum}(\mathbf{x} )}{\partial \mathbf{x} } =\mathbf{1}^{\text{T} } ∂x∂sum(x)=1T 可得)
x.grad_zero_()
y = x * x
y.sum().backward() # 等价于 y.backward(torch.ones(len(x)))
x.grad # tensor([0., 2., 4., 6.])
【例4】构建如下函数的计算图需经过Python控制流,计算变量的梯度
def f(a):
b = a * 2
while b.norm() < 1000:
b *= 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
a = torch.randn(size=(), requires_grad=True)
d = f(a) # d实为关于a的线性函数,因此梯度即为该直线的斜率
d.backward()
a.grad == d / a # tensor(True)
6 概率
6.1 基本概率论
抽样(Sampling)是统计学中把从概率分布中抽取样本的过程。分布(Distribution)可以视作是对事件(Event)的概率分配,将概率分配给一些离散选择的分布称为多项分布(Multinomial Distribution)。随机变量(Random Variable)可以在随机实验的一组可能性中取一个值。
事件(Event)是一组给定样本空间(Sample Space,或称结果空间,Outcome Space)的随机结果。若对于所有 i ≠ j i≠j i=j 都有 A i ∩ A j = ∅ \mathcal{A}_i \cap \mathcal{A}_j=\emptyset Ai∩Aj=∅ ,则称这两个事件互斥(Mutually Exclusive)。
概率(Probability)可以被认为是将集合映射到真实值的函数。在给定的样本空间 S \mathcal{S} S 中,事件 A \mathcal{A} A 的概率表示为 P ( A ) P(\mathcal{A}) P(A) 。概率满足以下3条概率论公理:
- 对于任意事件 A \mathcal{A} A ,其概率必定非负,即 P ( A ) ≥ 0 P(\mathcal{A})≥0 P(A)≥0
- 整个样本空间的概率为 1 1 1 ,即 P ( S ) = 1 P(\mathcal{S})=1 P(S)=1
- 对于互斥事件的任一可数序列 A 1 , A 2 , ⋯ \mathcal{A}_1,\mathcal{A}_2,\cdots A1,A2,⋯ ,序列中任意一个事件发生的概率等于它们各自发生的概率之和,即 P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup\limits_{i=1}^{\infin} \mathcal{A}_i)=\sum\limits_{i=1}^{\infin} P(\mathcal{A}_i) P(i=1⋃∞Ai)=i=1∑∞P(Ai)
6.2 多个随机变量的运算
6.2.1 联合概率
联合概率(Joint Probability) P ( A = a , B = b ) P(A=a,B=b) P(A=a,B=b) 表示同时满足 A = a A=a A=a 和 B = b B=b B=b 的概率,对于任意 a , b a,b a,b ,有 P ( A = a , B = b ) ≤ min ( P ( A = a ) , P ( B = b ) ) P(A=a,B=b)≤\min(P(A=a),P(B=b)) P(A=a,B=b)≤min(P(A=a),P(B=b))
6.2.2 条件概率
由联合概率的不等式可得 0 ≤ P ( A = a , B = b ) P ( A = a ) ≤ 1 0≤\frac{P(A=a,B=b)}{P(A=a)}≤1 0≤P(A=a)P(A=a,B=b)≤1。将上式中的比率称为条件概率(Conditional Probability),记为 P ( B = b ∣ A = a ) P(B=b \mid A=a) P(B=b∣A=a),即 P ( B = b ∣ A = a ) = P ( A = a , B = b ) P ( A = a ) P(B=b \mid A=a)=\frac{P(A=a,B=b)}{P(A=a)} P(B=b∣A=a)=P(A=a)P(A=a,B=b)
6.2.3 贝叶斯定理
Bayes定理(Bayes’ Theorem):根据乘法法则(multiplication rule )可得 P ( A , B ) = P ( B ∣ A ) P ( A ) P(A,B)=P(B\mid A)P(A) P(A,B)=P(B∣A)P(A) ,根据对称性可得 P ( A , B ) = P ( A ∣ B ) P ( B ) P(A,B)=P(A\mid B)P(B) P(A,B)=P(A∣B)P(B) ,设 P ( B ) > 0 P(B)>0 P(B)>0 ,则有 P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
6.2.4 求和法则
求和法则(Sum Rule):求 B B B 的概率相当于计算 A A A 的所有可能选择,并将所有选择的联合概率聚合在一起,即 P ( B ) = ∑ A P ( A , B ) P(B)=\sum_A P(A,B) P(B)=A∑P(A,B)该操作又称为边际化(Marginalization),边际化结果的概率或分布称为边际概率(Marginal Probability) 或边际分布(Marginal Distribution)。
6.2.5 独立性
如果事件 A A A 的发生跟事件 B B B 的发生无关,则称两个随机变量 A A A 和 B B B 是独立(Dependence)的,记为 A ⊥ B A \perp B A⊥B ,易得此时 P ( A ∣ B ) = P ( A ) P(A\mid B)=P(A) P(A∣B)=P(A)。在所有其他情况下,称 A A A 和 B B B 依赖(Independence)。
同理,若对于三个随机变量 A , B , C A,B,C A,B,C 有 P ( A , B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) P(A,B\mid C)=P(A\mid C)P(B\mid C) P(A,B∣C)=P(A∣C)P(B∣C) ,则称 A A A 和 B B B是 条件独立(Conditionally Independent)的,记为 A ⊥ B ∣ C A \perp B \mid C A⊥B∣C。
6.3 期望和方差
为了概括概率分布的关键特征,我们需要一些测量方法。
一个随机变量
X
X
X 的期望(expectation,或平均值,Average)表示为
E
[
X
]
=
∑
x
x
P
(
X
=
x
)
E[X]=\sum_x xP(X=x)
E[X]=x∑xP(X=x)当函数
f
(
x
)
f(x)
f(x) 的输入是从分布
P
P
P 中抽取的随机变量时,
f
(
x
)
f(x)
f(x) 的期望值为
E
x
∼
P
[
f
(
x
)
]
=
∑
x
f
(
x
)
P
(
x
)
E_{x\sim P}[f(x)]=\sum_xf(x)P(x)
Ex∼P[f(x)]=x∑f(x)P(x)方差(Variance)可以量化随机变量与其期望值的偏置,定义为
Var
[
X
]
=
E
[
(
X
−
E
[
X
]
)
2
]
=
E
[
X
2
]
−
E
2
[
X
]
\text{Var}[X]=E[(X-E[X])^2]=E[X^2]-E^2[X]
Var[X]=E[(X−E[X])2]=E[X2]−E2[X]方差的平方根称为标准差(Standard Deviation)。
随机变量函数
f
(
x
)
f(x)
f(x) 的方差衡量的是:当从该随机变量分布中采样不同值
x
x
x 时, 函数值偏离该函数的期望的程度,即
Var
[
f
(
x
)
]
=
E
[
(
f
(
x
)
−
E
[
f
(
x
)
]
)
2
]
\text{Var}[f(x)]=E[(f(x)-E[f(x)])^2]
Var[f(x)]=E[(f(x)−E[f(x)])2]
7 如何读论文
- title
- abstract
- introduction
- method
- experiments
- conclusion
第一遍:标题、摘要、结论。可以看一看方法和实验部分重要的图和表。这样可以花费十几分钟时间了解到论文是否适合你的研究方向。
第二遍:确定论文值得读之后,可以快速的把整个论文过一遍,不需要知道所有的细节,需要了解重要的图和表,知道每一个部分在干什么,圈出相关文献。觉得文章太难,可以读引用的文献。
第三遍:提出什么问题,用什么方法来解决这个问题。实验是怎么做的。合上文章,回忆每一个部分在讲什么。























 498
498











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










