《动手学深度学习》笔记——深度神经网络 DNN / 多层感知机 MLP
深度学习基础笔记 (1) :预备知识(张量、梯度、概率…)
深度学习基础笔记 (2) :深度神经网络 DNN
深度学习基础笔记 (3) :优化算法(梯度下降、冲量法、Adam…)
深度学习基础笔记 (4) :卷积神经网络 CNN
深度学习基础笔记 (5) :计算机视觉(目标检测、语义分割、样式迁移)
深度学习基础笔记 (6) :注意力机制、Transformer
深度学习PyTorch代码模板
文章目录
1 线性回归
1.1 线性模型
线性回归(Linear Regression)是对n维输入的加权,外加偏差,可以看做是单层神经网络。
给定 n n n 维特征输入 x ( i ) = [ x 1 , x 2 , ⋯ , x n ] T \mathbf{x}^{(i)} =[x_1,x_2,\cdots,x_n]^\text{T} x(i)=[x1,x2,⋯,xn]T , n n n 维权重 w = [ w 1 , w 2 , ⋯ , w n ] T \mathbf{w} =[w_1,w_2,\cdots,w_n]^\text{T} w=[w1,w2,⋯,wn]T ,标量偏差 b b b ,则预测值 y ^ \hat y y^ 为 y ^ ( i ) = w T x ( i ) + b \hat y^{(i)} =\mathbf{w}^\text{T}\mathbf{x}^{(i)} +b y^(i)=wTx(i)+b对于有多个样本的特征集合 X \mathbf{X} X,预测值 y ^ \mathbf{\hat y} y^ 为 y ^ = X w + b \mathbf{\hat y}=\mathbf{X}\mathbf{w}+b y^=Xw+b
net = nn.Sequential(nn.Linear(2, 1))
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
1.2 损失函数:均方差(L2损失)
损失函数(Loss Function)能够量化目标的实际值与预测值之间的差距。 通常选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为0。
均方差/L2损失(Mean Square Error, L2 Loss)是回归问题中最常用的损失函数。当样本 i i i 的预测值为 y ^ ( i ) \hat y^{(i)} y^(i) ,其相应的真实标签为 y ( i ) y^{(i)} y(i) ,其平方误差为 l ( i ) ( w , b ) = 1 2 ( y ^ ( i ) − y ( i ) ) 2 l^{(i)}(\mathbf{w},b)=\frac12(\hat y^{(i)}-y^{(i)})^2 l(i)(w,b)=21(y^(i)−y(i))2为了度量模型在整个数据集上的质量,需计算在训练集 n n n 个样本上的损失均值,即为均方误差 L ( w , b ) = 1 n ∑ i = 1 n l ( i ) ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w T x ( i ) + b − y ( i ) ) 2 = 1 2 n ∥ X w + b − y ∥ 2 L(\mathbf{w},b)=\frac1n\sum_{i=1}^n l^{(i)}(\mathbf{w},b)=\frac1n\sum_{i=1}^n\frac12(\mathbf{w}^\text{T}\mathbf{x}^{(i)}+b-y^{(i)})^2=\frac1{2n}\lVert \mathbf{Xw}+b-\mathbf{y}\rVert^2 L(w,b)=n1i=1∑nl(i)(w,b)=n1i=1∑n21(wTx(i)+b−y(i))2=2n1∥Xw+b−y∥2最小化损失来学习参数 w ∗ , b ∗ = arg min w , b L ( w , b ) \mathbf{w}^*,b^*=\argmin_{\mathbf{w},b} L(\mathbf{w},b) w∗,b∗=w,bargminL(w,b)
loss = nn.MSELoss()
1.3 解析解
线性回归的解可以用一个公式简单地表达出来, 这类解叫作解析解(Analytical Solution)或显示解。将偏置 b b b 合并到参数 w \mathbf{w} w 中,在包含所有参数的矩阵中附加一列,即 X ← [ X , 1 ] , w ← [ w , b ] T \mathbf{X}\leftarrow [\mathbf{X},\mathbf{1}],\ \mathbf{w}\leftarrow[\mathbf{w},b]^\text{T} X←[X,1], w←[w,b]T则损失函数可化为 L ( w ) = 1 2 n ∥ y − X w ∥ 2 L(\mathbf{w})=\frac1{2n}\lVert \mathbf{y}-\mathbf{Xw} \rVert^2 L(w)=2n1∥y−Xw∥2 ,为凸函数,故最优解 w ∗ \mathbf{w}^* w∗ 满足 ∂ ∂ w L ( w ) = 0 1 n ( y − X w ) T X = 0 w ∗ = ( X T X ) − 1 X T y \begin{align*} \frac{\partial }{\partial \mathbf{w} } L(\mathbf{w})&=0 \\ \frac1n(\mathbf{y}-\mathbf{Xw})^\text{T}\mathbf{X}&=0\\ \mathbf{w}^*&=(\mathbf{X}^\text{T}\mathbf{X})^{-1}\mathbf{X}^\text{T}\mathbf{y} \end{align*} ∂w∂L(w)n1(y−Xw)TXw∗=0=0=(XTX)−1XTy
1.4 基础优化算法:梯度下降
梯度下降(Gradient Descent):初始化模型参数的值(如随机初始化),计算损失函数(损失均值)关于模型参数的导数(梯度),不断地在损失函数递减的方向上更新参数来降低误差,即 ( w , b ) ← ( w , b ) − η ∂ ( w , b ) L ( w , b ) (\mathbf{w},b )\leftarrow(\mathbf{w},b)-η\partial_{(\mathbf{w},b)}L(\mathbf{w},b) (w,b)←(w,b)−η∂(w,b)L(w,b) 小批量随机梯度下降(Minibatch Stochastic Gradient Descent):为深度学习默认的求解方法。原始方法实际执行的效率可能会非常慢,因为在每一次更新参数之前须遍历整个数据集。因此在每次需要计算更新的时候随机抽取一个小批量 B \mathcal{B} B,即 ( w , b ) ← ( w , b ) − η ∣ B ∣ ∑ i ∈ B ∂ ( w , b ) l ( i ) ( w , b ) (\mathbf{w},b )\leftarrow(\mathbf{w},b)-\frac{η}{\mathcal{|B|} }\sum_{i\in \mathcal{B} }\partial_{(\mathbf{w},b)}l^{(i)}(\mathbf{w},b) (w,b)←(w,b)−∣B∣ηi∈B∑∂(w,b)l(i)(w,b)其中 η η η 为学习率(Learning Rate), ∣ B ∣ |\mathcal{B}| ∣B∣ 为批量大小(Batch Size),这种手动预先指定而非训练时调整的参数称为超参数(Hyperparameter)。
# 需设置参数和学习率
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
2 softmax回归
- 回归估计一个连续值
- 单连续数值输出
- 自然区间 R \mathbb{R} R
- 跟真实值的区别作为损失
- 分类预测一个离散类别
- 通常多个输出
- 输出 i i i 是预测为第 i i i 类的置信度
2.1 分类问题
- 回归(Regression)估计一个连续值
- 单连续数值输出
- 自然区间 R \mathbb{R} R
- 跟真实值的区别作为损失
- 分类(Classification)预测一个离散类别
- 通常多个输出
- 输出 i i i 是预测为第 i i i 类的置信度
独热编码(One-hot Encoding):是一个向量,分量和类别一样多, 类别对应的分量设置为 1 1 1 ,其他所有分量设置为 0 0 0 。假设真实类别为 y y y ,对类别进行一位有效编码,则独热编码为 y = [ y 1 , y 2 , ⋯ , y n ] T , y i = { 1 if i = y 0 otherwise \mathbf{y}=[y_1,y_2,\cdots,y_n]^\text{T},\ y_i=\begin{cases} 1 & \text{ if } i=y \\ 0 & \text{ otherwise } \end{cases} y=[y1,y2,⋯,yn]T, yi={10 if i=y otherwise
2.2 softmax运算
softmax回归也是一个单层神经网络,用于处理多类分类问题,需要和未规范化的输出 o = [ o 1 , o 1 , ⋯ , o n ] T \mathbf{o}=[o_1,o_1,\cdots,o_n]^\text{T} o=[o1,o1,⋯,on]T 一样多的仿射函数(Affine Function),每个输出对应的仿射函数及其向量表示分别为 o i = ∑ j x j w i j + b i , i = 1 , 2 , ⋯ , n o = W x + b o_i=\sum_{j} x_jw_{ij}+b_i,\ i=1,2,\cdots,n\\ \mathbf{o}=\mathbf{Wx}+\mathbf{b} oi=j∑xjwij+bi, i=1,2,⋯,no=Wx+b使用softmax函数得到每个类的预测置信度:将输出变换为非负数且总和为1,使得 y ^ = [ y ^ 1 , y ^ 2 , ⋯ , y ^ n ] T \mathbf{\hat y}=[\hat y_1,\hat y_2,\cdots,\hat y_n]^\text{T} y^=[y^1,y^2,⋯,y^n]T 中对于所有 i i i 都有 0 ≤ y ^ i ≤ 1 0≤\hat y_i≤1 0≤y^i≤1,且 ∑ i y i = 1 \sum\limits_i y_i = 1 i∑yi=1,如下式 y ^ = softmax ( o ) where y ^ i = exp ( o i ) ∑ k exp ( o k ) \mathbf{\hat y}=\text{softmax}(\mathbf{o}) \text{ where } \hat y_i=\frac{\exp(o_i)}{\sum\limits_k\exp(o_k)} y^=softmax(o) where y^i=k∑exp(ok)exp(oi)此时 y ^ \mathbf{\hat y} y^ 可视为一个正确的概率分布,因此将具有最大输出值的类别 arg max i y ^ i \argmax\limits_i \hat y_i iargmaxy^i 作为预测 y ^ \hat y y^,即 y ^ = arg max i y ^ i = arg max i o i \hat y=\argmax_i \hat y_i=\argmax_i o_i y^=iargmaxy^i=iargmaxoi
# PyTorch不会隐式地调整输入的形状,因此需在线性层前定义展平层来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10)) # softmax操作已整合进loss中
def init_weights(m):
"""初始化参数"""
if type(m) == nn.Linear: # 仅初始化全连接层
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights) # 对模型所有层操作
2.3 损失函数:交叉熵损失
交叉熵(Cross-entropy)常用来衡量两个概率的区别 H ( p , q ) = − ∑ i p i log q i H(\mathbf{p},\mathbf{q})=-\sum_i p_i\log q_i H(p,q)=−i∑pilogqi分类问题常将真实概率 y \mathbf{y} y 和预测概率 y ^ \mathbf{\hat y} y^ 的区别作为损失,因此常用交叉熵损失函数,如下式 l ( y , y ^ ) = − ∑ i y i log y ^ i l(\mathbf{y},\mathbf{\hat y})=-\sum_i y_i\log \hat y_i l(y,y^)=−i∑yilogy^i
# 该损失函数整合了softmax操作
loss = nn.CrossEntropyLoss()
交叉熵函数的梯度:利用softmax的定义,将上式变形、对未规范化的输出 o i o_i oi 求导得 l ( y , y ^ ) = − ∑ i y i log exp ( o i ) ∑ k exp ( o k ) = ∑ i y i log ∑ k exp ( o k ) − ∑ i y i o i = log ∑ k exp ( o k ) − ∑ i y i o i ∂ o i l ( y , y ^ ) = exp ( o i ) ∑ k exp ( o k ) − y i = softmax ( o ) i − y i \begin{align*} l(\mathbf{y},\mathbf{\hat y})= &-\sum_i y_i \log \frac{\exp(o_i)}{\sum\limits_k \exp(o_k)} \\ = &\sum_i y_i \log \sum_k \exp(o_k) -\sum_i y_io_i \\ = & \log \sum_k\exp(o_k)-\sum_iy_io_i \end{align*}\\ \partial_{o_i}l(\mathbf{y},\mathbf{\hat y})=\frac{\exp(o_i)}{\sum_k \exp(o_k)}-y_i=\text{softmax}(\mathbf{o})_i-y_i l(y,y^)===−i∑yilogk∑exp(ok)exp(oi)i∑yilogk∑exp(ok)−i∑yioilogk∑exp(ok)−i∑yioi∂oil(y,y^)=∑kexp(ok)exp(oi)−yi=softmax(o)i−yi其中 softmax ( o ) i \text{softmax}(\mathbf{o})_i softmax(o)i 表示预测 y ^ \mathbf{\hat y} y^ 的第 i i i 个分量(即 y ^ i \hat y_i y^i ,参考softmax定义式)。该梯度正为真实概率与预测概率的区别。
3 多层感知机
3.1 基本概念
感知机(Perceptron):是最早的AI模型之一。给定输入 x \mathbf{x} x 、权重 w \mathbf{w} w 、偏移 b b b ,感知机输出 o = σ ( ⟨ w , x ⟩ + b ) , σ ( x ) = { 1 if x > 0 − 1 otherwise o=\sigma(\left \langle \mathbf{w},\mathbf{x}\right \rangle +b),\ \sigma(x)=\begin{cases} 1 & \text{ if } x>0 \\ -1 & \text{ otherwise } \end{cases} o=σ(⟨w,x⟩+b), σ(x)={1−1 if x>0 otherwise 输出为二分类,求解算法等价于使用批量大小为1的梯度下降。不能拟合XOR函数。
多层感知机(Multilayer Perceptron, MLP):在网络中加入一定层数的隐藏层(Hidden Layer),将许多全连接层堆叠在一起。 每一层的输出称为隐藏表示(Hidden Representation)或隐藏(层)变量(Hidden(-layer) Variable),顺次输出到后一层直到生成最后的输出。
每个隐藏层都有自己的隐藏层权重
W
i
\mathbf{W}_i
Wi 和隐藏层偏置
b
i
\mathbf{b}_i
bi,一个MLP可表示为
h
=
σ
(
W
1
x
+
b
1
)
o
=
W
2
h
+
b
2
y
=
softmax
(
o
)
\begin{align*} \mathbf{h}&=\sigma(\mathbf{W}_1\mathbf{x}+\mathbf{b_1}) \\ \mathbf{o} &=\mathbf{W}_2\mathbf{h}+\mathbf{b_2} \\ \mathbf{y} & = \text{softmax}(\mathbf{o} ) \end{align*}
hoy=σ(W1x+b1)=W2h+b2=softmax(o)

net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weight)
3.2 常见激活函数
激活函数(Activation Function):在仿射变换之后对每个隐藏单元应用的函数,大多数都是非线性的,其输出被称为活性值(Activations)。用于发挥多层架构的潜力,防止将多层感知机退化成线性模型。
- 修正线性单元(Rectified Linear Unit,ReLU):仅保留正元素并丢弃所有负元素
定义: ReLU ( x ) = max ( 0 , x ) \text{ReLU}(x)=\max(0,x) ReLU(x)=max(0,x)
导数( x = 0 x=0 x=0 时不可导,此时常默认使用左导数): d d x ReLU ( x ) = { 0 if x < 0 1 if x > 0 \frac{\mathrm{d}}{\mathrm{d}x}\text{ReLU}(x)=\begin{cases} 0 & \text{ if } x<0 \\ 1 & \text{ if } x>0 \end{cases} dxdReLU(x)={01 if x<0 if x>0
变体:参数化ReLU(Parameterized ReLU,pReLU)为ReLU添加了一个线性项,即使参数是负的,某些信息仍然可以通过 pReLU ( x ) = max ( 0 , x ) + α min ( 0 , x ) \text{pReLU}(x)=\max(0,x)+\alpha \min(0,x) pReLU(x)=max(0,x)+αmin(0,x) - Sigmoid函数:输入压缩到区间
(
0
,
1
)
(0, 1)
(0,1) 中的某个值,因此通常称为挤压函数(squashing function)
定义: sigmoid ( x ) = 1 1 + exp ( − x ) \text{sigmoid}(x)=\frac1{1+\exp(-x)} sigmoid(x)=1+exp(−x)1

导数: d d x sigmoid ( x ) = exp ( − x ) ( 1 + exp ( − x ) ) 2 = sigmoid ( x ) ( 1 − sigmoid ( x ) ) \frac{\mathrm{d}}{\mathrm{d}x}\text{sigmoid}(x)=\frac{\exp(-x)}{(1+\exp(-x))^2}=\text{sigmoid}(x)(1-\text{sigmoid}(x)) dxdsigmoid(x)=(1+exp(−x))2exp(−x)=sigmoid(x)(1−sigmoid(x))

- 双曲正切函数(tanh):将输入压缩转换到区间
(
−
1
,
1
)
(-1, 1)
(−1,1)上
定义: tanh ( x ) = 1 − exp ( − 2 x ) 1 + exp ( − 2 x ) \tanh(x)=\frac{1-\exp(-2x)}{1+\exp(-2x)} tanh(x)=1+exp(−2x)1−exp(−2x)
导数: d d x tanh ( x ) = 1 − tanh 2 ( x ) \frac{\mathrm{d}}{\mathrm{d}x}\tanh(x)=1-\tanh^2(x) dxdtanh(x)=1−tanh2(x)
3.3 模型选择、欠拟合和过拟合
训练误差(Training Error):模型在训练数据上的误差
泛化误差(Generalization Error):模型在新数据上的误差
验证数据集(Validation Dataset):用来评估模型好坏的数据集(不应跟训练数据混在一起)
测试数据集(Test Dataset):只用一次的数据集
K K K折交叉验证:在没有足够多数据时使用。将训练数据分割成 K K K 块;执行 K K K 次模型训练与验证,每轮迭代使用其中1块作为验证数据集,其余的作为训练数据;最后报告 K K K 个验证集误差的平均值。常取 K = 5 K=5 K=5 或 10 10 10

模型容量(模型复杂性):拟合各种函数的能力,需要匹配数据复杂度(取决于多个重要因素——样本个数、每个样本的元素个数、时间/空间结构、多样性)。
- 低容量的模型难以拟合训练数据——欠拟合(Underfitting)
- 高容量的模型可以记住所有的训练数据——过拟合(Overfitting)。
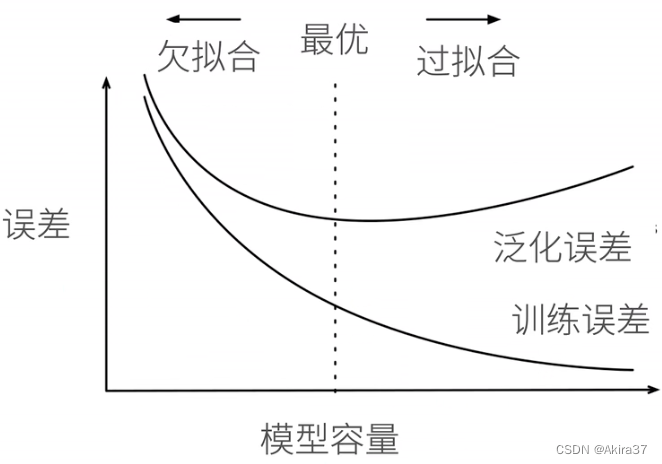
VC维:统计学习理论的一个核心思想。对于一个分类模型,VC等于一个最大的数据集的大小,不管如何给定标号,都存在一个模型来对它进行完美分类。
【例】2维输入的感知机,VC维=3 —— 能够分类任何3个点,但不是4个(xor)。如下图所示

- 支持 N N N 维输入的感知机的VC维是 N + 1 N+ 1 N+1
- 一些多层感知机的VC维 O ( N log 2 N ) O(N\log_2 N) O(Nlog2N)
- 在深度学习中很少使用,因为衡量不是很准确,且计算深度学习模型的VC维很困难(
3.4 权重衰退(L2正则化)
权重衰退/ L 2 L_2 L2正则化(Weight Decay)是最广泛使用的正则化的技术之一,通过 L 2 L_2 L2正则项使得模型参数不会过大,从而控制模型复杂度。
硬性限制:直接限制参数值的选择范围 θ \theta θ 来控制模型容量(通常没必要限制偏移 b b b),越小的 θ \theta θ 意味着更强的正则项,即 min L ( w , b ) subject to ∥ w ∥ 2 ≤ θ \min L(\mathbf{w},b) \text{ subject to } \lVert \mathbf{w} \rVert ^2≤\theta minL(w,b) subject to ∥w∥2≤θ
柔性限制:在上式的基础上,对每个
θ
\theta
θ ,都可以找到正则化常数
λ
\lambda
λ,控制
L
2
L_2
L2正则项
∥
w
∥
2
\lVert \mathbf{w} \rVert^2
∥w∥2 的重要程度:
λ
=
0
\lambda=0
λ=0 时无作用;
λ
→
∞
\lambda \rightarrow \infin
λ→∞ 时
w
∗
→
0
\mathbf{w}^* \rightarrow \mathbf{0}
w∗→0。即使用验证数据拟合
L
(
w
,
b
)
+
λ
2
∥
w
∥
2
L(\mathbf{w},b) + \frac \lambda 2 \lVert \mathbf{w} \rVert ^2
L(w,b)+2λ∥w∥2根据上式进行梯度下降、更新权重(通常
η
λ
<
1
\eta \lambda<1
ηλ<1):
∂
∂
w
(
l
(
w
,
b
)
+
λ
2
∥
w
∥
2
)
=
∂
l
(
w
,
b
)
∂
w
+
λ
w
w
←
w
−
η
∂
∂
w
(
l
(
w
,
b
)
+
λ
2
∥
w
∥
2
)
=
(
1
−
η
λ
)
w
−
η
∂
l
(
w
,
b
)
∂
w
\frac{\partial }{\partial \mathbf{w} }(l(\mathbf{w},b)+\frac \lambda 2 \lVert \mathbf{w} \rVert ^2)=\frac{\partial l(\mathbf{w},b)}{\partial \mathbf{w}}+\lambda\mathbf{w}\\ \mathbf{w}\leftarrow \mathbf{w}-\eta \frac{\partial }{\partial \mathbf{w} }(l(\mathbf{w},b)+\frac \lambda 2 \lVert \mathbf{w} \rVert ^2)= (1-\eta \lambda)\mathbf{w}-\eta \frac{\partial l(\mathbf{w},b)}{\partial \mathbf{w}}
∂w∂(l(w,b)+2λ∥w∥2)=∂w∂l(w,b)+λww←w−η∂w∂(l(w,b)+2λ∥w∥2)=(1−ηλ)w−η∂w∂l(w,b)
3.5 丢弃法(Dropout)
丟弃法/暂退法(Dropout):在层之间加入噪音,根据超参数丢弃概率
p
p
p (常取0.5, 0.9, …)将一些输出项随机置0来控制模型复杂度。若对
x
\mathbf{x}
x 加入噪音得到
x
′
\mathbf{x'}
x′ ,期望
E
[
x
′
]
=
x
E[\mathbf{x'}]=\mathbf{x}
E[x′]=x ,则对每个元素进行如下扰动
x
i
′
=
dropout
(
x
i
)
=
{
0
with probability
p
x
i
1
−
p
otherwise
x_i'=\text{dropout}(x_i)=\begin{cases} 0 & \text{ with probability } p \\ \frac{x_i}{1-p} & \text{ otherwise } \end{cases}
xi′=dropout(xi)={01−pxi with probability p otherwise 通常将丟弃法作用在隐藏全连接层的输出上
h
=
σ
(
W
1
x
+
b
1
)
h
′
=
dropout
(
h
)
o
=
W
2
h
′
+
b
2
y
=
softmax
(
o
)
\begin{align*} \mathbf{h}&=\sigma(\mathbf{W}_1\mathbf{x}+\mathbf{b_1}) \\ \mathbf{h'} &= \text{dropout}(\mathbf{h})\\ \mathbf{o} &=\mathbf{W}_2\mathbf{h'}+\mathbf{b_2} \\ \mathbf{y} & = \text{softmax}(\mathbf{o} ) \end{align*}
hh′oy=σ(W1x+b1)=dropout(h)=W2h′+b2=softmax(o)
dropout是正则项,只在训练中使用,影响模型参数的更新。在推理过程中,dropout直接返回输入,这样也能保证确定性的输出,即 h = dropout ( h ) \mathbf{h} = \text{dropout}(\mathbf{h}) h=dropout(h)
PyTorch实现:nn.Dropout(丢弃概率p)
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
# 在第一个全连接层之后添加一个dropout层
nn.Dropout(dropout1),
nn.Linear(256, 256),
nn.ReLU(),
# 在第二个全连接层之后添加一个dropout层
nn.Dropout(dropout2),
nn.Linear(256, 10))
3.6 数值稳定性和模型初始化
设一个深度神经网络(Dense/Deep Neural Network,DNN)具有 L L L 层,输入为 x \mathbf{x} x ,输出为 o \mathbf{o} o ,第 l l l 层由权重为 W ( l ) \mathbf{W}^{(l)} W(l) 、隐藏变量为 h ( l ) \mathbf{h}^{(l)} h(l) 的变换 f l f_l fl 定义(令 h ( 0 ) = x \mathbf{h}^{(0)}=\mathbf{x} h(0)=x),则可表示为 h ( l ) = f l ( h ( l − 1 ) ) hence o = f L ∘ f L − 1 ∘ ⋯ ∘ f 1 ( x ) \mathbf{h}^{(l)}=f_l(\mathbf{h}^{(l-1)}) \text{ hence } \mathbf{o}=f_L \circ f_{L-1} \circ \cdots \circ f_1(\mathbf{x}) h(l)=fl(h(l−1)) hence o=fL∘fL−1∘⋯∘f1(x)若所有隐藏变量和输入都是向量, 则可将输出 o \mathbf{o} o 关于任意一组参数 W ( l ) \mathbf{W}^{(l)} W(l) 的梯度表示为 ∂ W ( l ) o = ∂ h ( L − 1 ) h ( L ) ∂ h ( L − 2 ) h ( L − 1 ) ⋯ ∂ h ( l + 1 ) h ( l + 2 ) ∂ h ( l ) h ( l + 1 ) ∂ W ( l ) h ( l ) \partial_{\mathbf{W}^{(l)}}\mathbf{o}=\partial_{\mathbf{h}^{(L-1)}}\mathbf{h}^{(L)} \partial_{\mathbf{h}^{(L-2)}}\mathbf{h}^{(L-1)} \cdots \partial_{\mathbf{h}^{(l+1)}}\mathbf{h}^{(l+2)} \partial_{\mathbf{h}^{(l)}}\mathbf{h}^{(l+1)} \partial_{\mathbf{W}^{(l)}}\mathbf{h}^{(l)} ∂W(l)o=∂h(L−1)h(L)∂h(L−2)h(L−1)⋯∂h(l+1)h(l+2)∂h(l)h(l+1)∂W(l)h(l)由上式易知,深度神经网络的梯度是 L − l L-l L−l 个矩阵与1个梯度向量的乘积,如此多项的乘积可能非常大,也可能非常小,使得出现不稳定梯度,极易产生以下两种数值稳定性问题:
- 梯度爆炸(Gradient Exploding):参数更新过大,破坏了模型的稳定收敛
- 值超出值域:对于16位浮点数尤为严重(数值区间
6e-5~6e4) - 对学习率敏感,可能需在训练过程中不断调整学习率
- 学习率太大→大参数值→更大的梯度
- 学习率太小→训练无进展
- 值超出值域:对于16位浮点数尤为严重(数值区间
- 梯度消失(Gradient Vanishing): 参数更新过小,在每次更新时几乎不会移动,导致模型无法学习
- 梯度值变成0:对16位浮点数尤为严重
- 训练没有进展,不管如何选择学习率
- 对于底部层尤为严重:仅仅顶部层训练的较好,无法让神经网络更深
让训练更加稳定:
- 让梯度值在合理的范围内。(例如在
[1e-6, 1e3]上)- 将乘法变加法(ResNet、LSTM)
- 归一化(梯度归一化、梯度裁剪)
- 合理的权重初始和激活函数
- 让每层的方差是一个常数:将每层的输出和梯度都看做随机变量,让它们的均值和方差都保持一致
解决(或至少减轻)数值稳定性问题的一种方法是进行合理的参数初始化。通常可用正态分布初始化权重,或直接使用框架默认的随机初始化方法。(参考前述各种网络模型)
Xavier初始化:对于没有非线性的全连接层(如隐藏层),其共有 n in n_\text{in} nin 个输入、 n out n_\text{out} nout 个输出,第 j j j 个输入 x j x_j xj 的权重为 w i j w_{ij} wij ,则第 i i i 个输出 o i o_i oi可表示为 o i = ∑ j = 1 n in w i j x j o_i=\sum_{j=1}^{n_\text{in}}w_{ij}x_j oi=j=1∑ninwijxj假设权重 w i j w_{ij} wij 从均值为 0 0 0 、方差为 σ 2 \sigma^2 σ2 的同一分布中独立抽取,输入层全体 x j x_j xj 也满足均值为 0 0 0 、方差为 γ 2 \gamma^2 γ2 且与 w i j w_{ij} wij 彼此独立,则可计算得 o i o_i oi 的均值和方差为 E [ o i ] = ∑ j = 1 n in E [ w i j x j ] = ∑ j = 1 n in E [ w i j ] E [ x j ] = 0 Var [ o i ] = E [ o i 2 ] − E 2 [ o i ] = ∑ j = 1 n in E [ w i j 2 x j 2 ] − 0 = ∑ j = 1 n in E [ w i j 2 ] E [ x j 2 ] = n in σ 2 γ 2 E[o_i]=\sum_{j=1}^{n_\text{in}}E[w_{ij}x_j]=\sum_{j=1}^{n_\text{in}}E[w_{ij}]E[x_j]=0\\ \text{Var}[o_i]=E[o_i^2]-E^2[o_i]=\sum_{j=1}^{n_\text{in}}E[w_{ij}^2x_j^2]-0=\sum_{j=1}^{n_\text{in}}E[w_{ij}^2]E[x_j^2]=n_\text{in}\sigma^2\gamma^2 E[oi]=j=1∑ninE[wijxj]=j=1∑ninE[wij]E[xj]=0Var[oi]=E[oi2]−E2[oi]=j=1∑ninE[wij2xj2]−0=j=1∑ninE[wij2]E[xj2]=ninσ2γ2要想保持方差始终为 γ 2 \gamma^2 γ2 不变,需设置 n in σ 2 = 1 n_\text{in}\sigma^2=1 ninσ2=1 。反向传播同理,参考上述前向传播的推断过程可知需设置 n out σ 2 = 1 n_\text{out}\sigma^2=1 noutσ2=1 。显然无法同时满足这两个条件。Xavier初始化只需满足以下条件: 1 2 ( n in + n out ) σ 2 = 1 ⇔ σ = 2 n in + n out \frac12(n_\text{in}+n_\text{out})\sigma^2=1 \Leftrightarrow \sigma=\sqrt{\frac2{n_\text{in}+n_\text{out}}} 21(nin+nout)σ2=1⇔σ=nin+nout2通常Xavier初始化从均值为 0 0 0 、方差为 σ 2 = 2 n in + n out \sigma^2=\frac2{n_\text{in}+n_\text{out}} σ2=nin+nout2 的高斯分布中采样权重。也可以改为选择从均匀分布中抽取权重时的方差,由均匀分布 U ( − a , a ) U(-a,a) U(−a,a) 的方差为 a 3 3 \frac{a^3}3 3a3 ,代入上式可得Xavier初始化值域为 U ( − 6 n in + n out , 6 n in + n out ) U(-\sqrt{\frac6{n_\text{in}+n_\text{out}}},\sqrt{\frac6{n_\text{in}+n_\text{out}}}) U(−nin+nout6,nin+nout6)
4 深度学习计算
4.1 层和块
一个块可以由许多层或块组成。块可以包含代码,负责大量的内部处理,包括参数初始化和反向传播。层和块的顺序连接可以由Sequential块处理。
import torch
import torch.nn.functional as F
from torch import nn
class MLP(nn.Module):
def __init__(self):
super().__init__()
self.net = nn.Sequential(nn.Linear(20, 64), nn.ReLU(),
nn.Linear(64, 32), nn.ReLU())
self.linear = nn.Linear(32, 16)
def forward(self, X):
return self.linear(self.net(X))
net = MLP()
y_hat = net(X)
4.2 参数管理
Sequential内部组织
4.2.1 参数访问
直接打印可得Sequential类的内部组织:
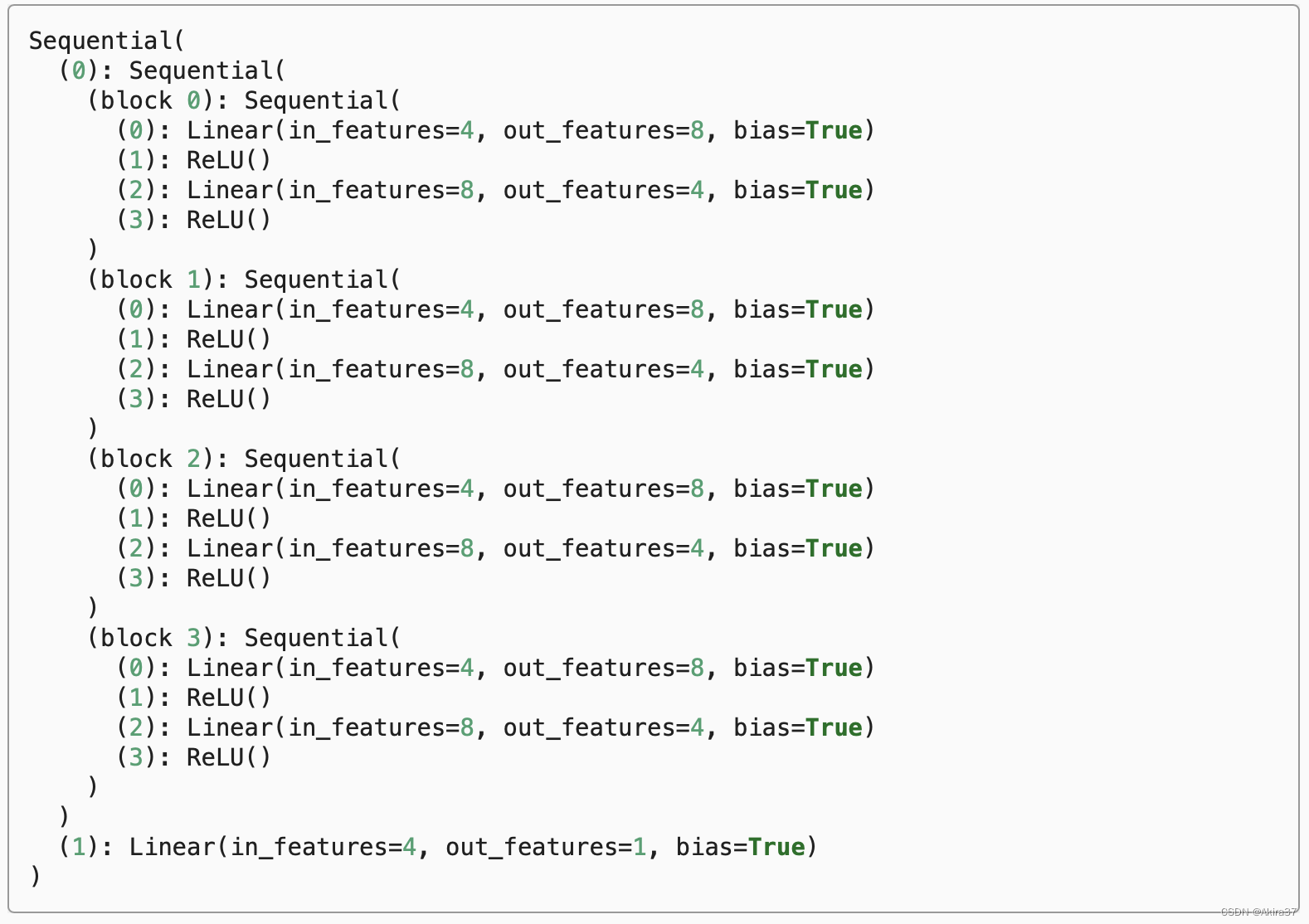
Sequential类相当于列表,可以直接用索引访问对应的层。对于嵌套块,因为层是分层嵌套的,所以也可以像通过嵌套列表索引一样访问它们。相关方法和成员参见前文。
# 获取参数的名称及其值的字典
net[2].state_dict() # 返回OrderedDict类型
# 访问参数及其成员
net[2].bias # 获取偏移(包含值和其他信息)
rgnet[0][1][0].bias.data # 获取偏移的值
net[2].weight.grad # 获取权值的梯度
# 一次性访问所有参数
[(name, param.shape) for name, param in net[0].named_parameters()] # 访问0号层的所有参数
[(name, param.shape) for name, param in net.named_parameters()] # 访问整个网络所有层的所有参数
4.2.2 参数初始化
默认情况下,PyTorch会根据一个范围均匀地初始化权重和偏置矩阵, 这个范围是根据输入和输出维度计算出的。
- 内置初始化:调用PyTorch的
nn.init模块提供的初始化函数
# 初始化为标准正态分布
def init_normal(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, mean=0, std=0.01)
nn.init.zeros_(m.bias)
net.apply(init_normal)
# 初始化为常数1
def init_constant(m):
if type(m) == nn.Linear:
nn.init.constant_(m.weight, 1)
nn.init.zeros_(m.bias)
net.apply(init_constant)
# 对不同块应用不同的初始化方法:对0号层用Xavier初始化,对2号层初始化为常数42
def init_xavier(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
def init_42(m):
if type(m) == nn.Linear:
nn.init.constant_(m.weight, 42)
net[0].apply(init_xavier)
net[2].apply(init_42)
- 自定义初始化:当深度学习框架没有提供实际需要的初始化方法时可自定义初始化方法。
【例】使用以下的分布为任意权重参数 w w w 定义初始化方法 w ∼ { U ( 5 , 10 ) with probability 1 4 0 with probability 1 2 U ( − 10 , − 5 ) with probability 1 4 w\sim \begin{cases} U(5,10) & \text{ with probability } \frac14 \\ 0 & \text{ with probability } \frac12 \\ U(-10,-5) & \text{ with probability } \frac14 \end{cases} w∼⎩ ⎨ ⎧U(5,10)0U(−10,−5) with probability 41 with probability 21 with probability 41
# 自定义初始化
def my_init(m):
if type(m) == nn.Linear:
print("Init", *[(name, param.shape)
for name, param in m.named_parameters()][0])
nn.init.uniform_(m.weight, -10, 10)
m.weight.data *= m.weight.data.abs() >= 5
net.apply(my_init)
- 直接初始化!
net[0].weight.data[:] += 1
net[0].weight.data[0, 0] = 42
net[0].weight.data[0]
4.2.3 参数绑定
在Sequential外定义共享层变量,在Sequential中的多个层间共享参数
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
shared, nn.ReLU(),
shared, nn.ReLU(),
nn.Linear(8, 1))
4.3 自定义层
有时会遇到或要自己发明一个现在在深度学习框架中还不存在的层。 在这些情况下,必须构建自定义层。可以将自定义层像预置层一样作为组件合并到更复杂的模型中。
构造不带参数的层:
class CenteredLayer(nn.Module):
"""从其输入中减去均值的层"""
def __init__(self):
super().__init__()
def forward(self, X):
return X - X.mean()
layer = CenteredLayer()
net = nn.Sequential(nn.Linear(8, 128), CenteredLayer())
构建带参数的层:
class MyLinear(nn.Module):
"""自定义版的全连接层"""
def __init__(self, in_units, units):
super().__init__()
self.weight = nn.Parameter(torch.randn(in_units, units))
self.bias = nn.Parameter(torch.randn(units,))
def forward(self, X):
linear = torch.matmul(X, self.weight.data) + self.bias.data
return F.relu(linear)
linear = MyLinear(5, 3)
net = nn.Sequential(MyLinear(64, 8), MyLinear(8, 1))
4.4 读写文件
加载和保存张量
x = torch.arange(4)
y = torch.zeros(4)
mydict = {'x': x, 'y': y}
# 保存或读取张量
torch.save(x, 'x-file')
x2 = torch.load('x-file')
# 保存或读取张量列表
torch.save([x, y], 'x-files')
x2, y2 = torch.load('x-files')
# 保存或读取从字符串映射到张量的字典
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')
加载和保存模型参数
net = MLP() # 4.1的MLP网络
# 存储网络:存参数的字典
torch.save(net.state_dict(), 'mlp.params')
# 读取网络(需先定义相同类的网络)
clone = MLP()
clone.load_state_dict(torch.load('mlp.params'))
























 1863
1863

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










