基于深度神经网络的人体姿态估计算法——DeepPose
参考
简介
Attention 1. 在本文中,人姿态估计=关键点检测=人体骨骼点检测; 2. 这是一种单人关键点检测算法,因此假设一张图仅有一个人的关节点需要进行预测。3. 本文为作者自己的理解,仅供参考。
DeepPose是第一个将深度神经网络(DNN)应用于人体关键点检测的算法框架。在FLIC和LSP数据集上取得了当时最好的检测精度。同时他也是第一个将关键点检测问题转换为回归问题的算法,通过级联的多个DNN网络,直接回归关节点的坐标值。其后的所有主流姿态估计算法基本都是基于这个算法的思想进行的改进或创新。本文首先介绍算法框架的一些预处理,其次介绍真个网络结构。
关键点坐标的表示方式
假设需要检测的骨骼点有
k
k
k 个,关键点在图片中的绝对坐标值为
y
=
(
.
.
.
,
y
i
T
,
.
.
.
)
,
i
∈
(
i
,
.
.
.
,
k
)
\bold{y} = (..., \bold{y}_{i}^{T}, ...), i \in (i, ..., k)
y=(...,yiT,...),i∈(i,...,k) ,其中
y
i
T
\bold{y}_{i}^{T}
yiT 表示第
i
i
i 个关键点的坐标值
(
x
i
,
y
i
)
(x_i, y_i)
(xi,yi) 。因为算法回归的是关节点的坐标值,因此如果直接回归关节点在图片中的绝对坐标值,那么就会存在scale的问题。即同样大小的输入图片,如果人的相对于图片的scale差距过大,那么关节点坐标值的差距也会很大。因此作者首先对关节点的直接坐标值进行了归一化处理。设人体的bounding box 表示为
b
=
(
b
c
,
b
w
,
b
h
)
\bold{b} = (\bold{b}_{c}, b_w, b_h)
b=(bc,bw,bh) ,其中
b
c
=
(
c
x
,
c
y
)
\bold{b}_{c}=(c_x,c_y)
bc=(cx,cy) 表示bounding box的中心点(bounding box可以通过关节点的绝对坐标值计算出来)。那么归一化的关节点坐标(相对坐标)表示如下:
(1)
N
(
y
i
;
b
)
=
(
1
/
b
w
0
0
1
/
b
h
)
(
y
i
−
b
c
)
N\left(\mathbf{y}_{i} ; b\right)=\left( \begin{array}{cc}{1 / b_{w}} & {0} \\ {0} & {1 / b_{h}}\end{array}\right)\left(\mathbf{y}_{i}-b_{c}\right) \tag{1}
N(yi;b)=(1/bw001/bh)(yi−bc)(1)
经过归一化后的关节点坐标,对于scale的变化具有更好的鲁棒性,同时降低了回归的值的范围,降低了网络训练的难度。由 (1) 可以得到网络预测的关节点坐标相对于图片的绝对位置为
(2)
y
∗
=
N
−
1
(
ψ
(
N
(
x
)
;
θ
)
)
y^{*}=N^{-1}(\psi(N(x) ; \theta)) \tag{2}
y∗=N−1(ψ(N(x);θ))(2)
网络结构
整体网络结构如下所示:
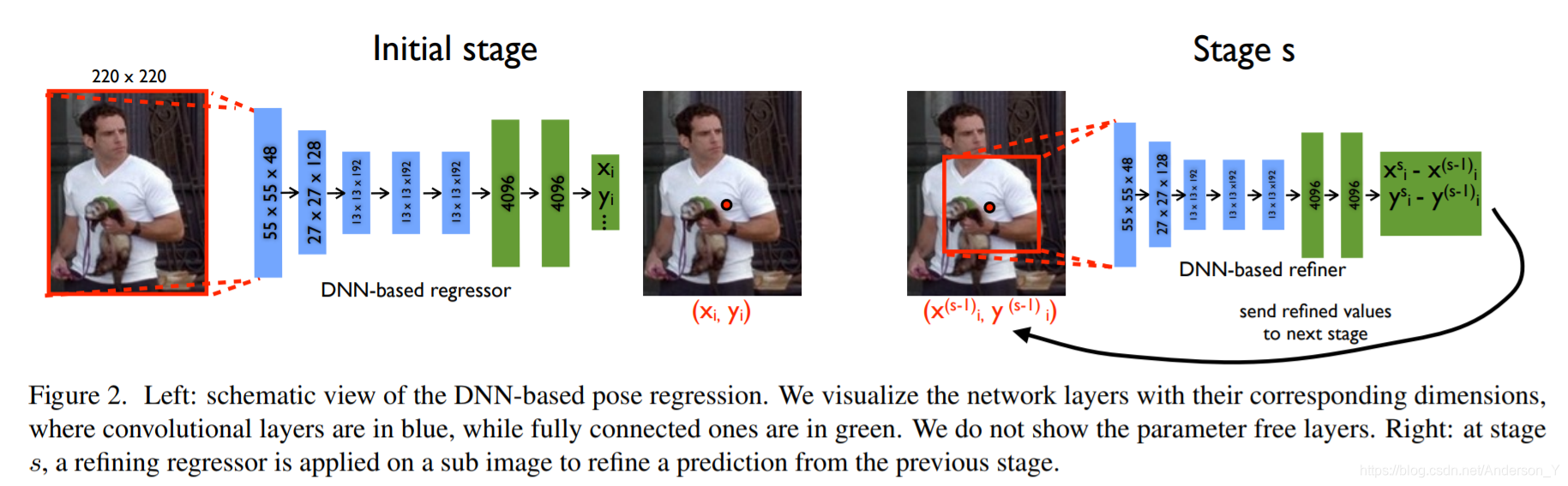
Attention 后文中,我们使用 C C C 表示卷积层, P P P 表示池化层, F F F 表示全连接层, L R C LRC LRC 表示局部响应归一化层(Local Response Normalization)。其中只有 C C C 和 F F F 的参数需要训练,其余层参数都是不需要训练的。关于LRN,参考论文 ImageNet Classification with Deep Convolutional Neural Networks 3.3
Initial Stage
上图左边为Initial Stage,其中蓝色表示 C C C ,绿色标识 F F F ,其余的层没有画出来。Initial Stage的详细网络结构如下所示:

| Name | Filter Size(WHC)/Stride | Input Shape(WHC) | Output |
|---|---|---|---|
| Conv | 11x11x96/4 | 224x224x3 | 55x55x96 |
| LRN | None | 55x55x96 | 55x55x96 |
| MaxP | 2x2/2 | 55x55x96 | 27x27x96 |
| Conv | 5x5x256/1 | 27x27x96 | 27x27x256 |
| LRN | None | 27x27x256 | 27x27x256 |
| MaxP | 2x2/2 | 27x27x256 | 13x13x256 |
| Conv | 3x3x384/1 | 13x13x256 | 13x13x384 |
| Conv | 3x3x384/1 | 13x13x384 | 13x13x384 |
| Conv | 3x3x256/1 | 13x13x384 | 13x13x256 |
| MaxP | 2x2/2 | 13x13x256 | 6x6x256 |
| Flatten | None | 6x6x256 | 4096x1 |
| F | None | 4096x1 | 4096x1 |
| F | None | 4096x1 | 4096x1 |
| F | None | 4096x1 | 2xk |
Attention 训练时,所有 F F F 层采用Dropout=0.6
设一个batch表示为
D
N
D_{N}
DN :
(3)
D
N
=
{
(
N
(
x
)
,
N
(
y
)
)
∣
(
x
,
y
)
∈
D
}
D_{N}=\{(N(x), N(\mathbf{y})) |(x, \mathbf{y}) \in D\} \tag{3}
DN={(N(x),N(y))∣(x,y)∈D}(3)
这部分网路的损失函数采用归一化后的关节点坐标
N
(
y
;
b
)
N(\bold{y};b)
N(y;b) 和预测的关节点坐标
ψ
(
y
;
b
)
\psi_(\bold{y};b)
ψ(y;b) 之间的L2距离作为损失函数。数学表达式如:
(4)
arg
min
θ
∑
(
x
,
y
)
∈
D
N
∑
i
=
1
k
∥
y
i
−
ψ
i
(
x
;
θ
)
∥
2
2
\arg \min _{\theta} \sum_{(x, y) \in D_{N}} \sum_{i=1}^{k}\left\|\mathbf{y}_{i}-\psi_{i}(x ; \theta)\right\|_{2}^{2} \tag{4}
argθmin(x,y)∈DN∑i=1∑k∥yi−ψi(x;θ)∥22(4)
对于没有label的关节点,可以通过将其加权系数置零来达忽略其预测的输出。
Cascade
Initial Stage模型存在一个问题,就是因为初始卷积核为 11x11,虽然卷积核感受野很大,但是难以捕捉到一些关节点周围的细节(contextual details),这些细节对于精确定位是很重要的。虽然可以通过提高输入图片的分辨率来解决这个问题,但是这样会极大的提高训练的参数数量。于是作者提出了级联的DNN模型。首先通过Initial Stage提取比较粗略的关节点位置,然后再训练一个分类器,用来从粗略的关节点位置回归精确的关节点位置,即对initial stage的输出做refine操作,从而得到更加准确的结果。示意图如图1-左所示。这部分的网络结构采用和initial stage 部分相同的网络结构。
对于stage
s
∈
(
1
,
.
.
.
,
S
)
s\in(1, ..., S)
s∈(1,...,S) ,设该stage需要训练的参数为
θ
s
\theta_{s}
θs ,则该stage的输出为
ψ
(
x
;
θ
s
)
\psi(x;\theta_{s})
ψ(x;θs) 。为了对一个给定的关节点位置
y
i
\bold{y}_{i}
yi 进行refine,需要一个以
y
i
\bold{y}_{i}
yi 为中心的 joint bounding box :
b
i
(
y
;
σ
)
=
(
y
i
,
σ
∗
d
i
a
m
(
y
)
,
σ
∗
d
i
a
m
(
y
)
)
b_i(\bold{y};\sigma)=(\bold{y}_i, \sigma*diam(\bold{y}), \sigma*diam(\bold{y}))
bi(y;σ)=(yi,σ∗diam(y),σ∗diam(y)) ,其中
d
i
a
m
(
y
)
diam(\bold{y})
diam(y) 表示关节点
y
\bold{y}
y 中相对应的关节点之间的距离,例如左肩膀和右肩膀之间的距离,其定义依赖于数据集。使用
b
i
b_i
bi 从原图裁剪子图,作为
s
s
s 阶段的输入。使用上述符号,则可以将initial stage描述为:
(5)
S
t
a
g
e
1
:
y
1
←
N
−
1
(
ψ
(
N
(
x
;
b
0
)
;
θ
1
)
;
b
0
)
Stage \ 1 : \quad \mathbf{y}^{1} \leftarrow N^{-1}\left(\psi\left(N\left(x ; b^{0}\right) ; \theta_{1}\right) ; b^{0}\right) \tag{5}
Stage 1:y1←N−1(ψ(N(x;b0);θ1);b0)(5)
其中
b
0
b^0
b0 表示整个输入图像的bounding box 。
对于
s
≥
2
s\ge2
s≥2 的stage,该阶段的预测一个displacement:
y
i
s
−
y
i
s
−
1
\bold{y}_{i}^{s}-\bold{y}_{i}^{s-1}
yis−yis−1 ,因此第
s
s
s stage 预测的关节点坐标为:
(6)
S
t
a
g
e
s
:
y
i
s
←
y
i
(
s
−
1
)
+
N
−
1
(
ψ
i
(
N
(
x
;
b
)
;
θ
s
)
;
b
)
Stage \ s : \quad \mathbf{y}_{i}^{s} \leftarrow \mathbf{y}_{i}^{(s-1)}+N^{-1}\left(\psi_{i}\left(N(x ; b) ; \theta_{s}\right) ; b\right) \tag{6}
Stage s:yis←yi(s−1)+N−1(ψi(N(x;b);θs);b)(6)
其中
b
=
b
i
(
s
−
1
)
b=b_i^{(s-1)}
b=bi(s−1) ,表示根据
s
−
1
s-1
s−1 stage 的预测计算得到的 joint bounding box 。
然后更新 joint bounding box :
(7)
b
i
s
←
(
y
i
s
,
σ
diam
(
y
s
)
,
σ
diam
(
y
s
)
)
b_{i}^{s} \leftarrow\left(\mathbf{y}_{i}^{s}, \sigma \operatorname{diam}\left(\mathbf{y}^{s}\right), \sigma \operatorname{diam}\left(\mathbf{y}^{s}\right)\right) \tag{7}
bis←(yis,σdiam(ys),σdiam(ys))(7)
为了防止过拟合,作者还对中间数据进行了增强。这一步并没有弄得很清楚,请参看原文3.2节。cascade的stage的目标函数为:
(8)
θ
s
=
arg
min
θ
∑
(
x
,
y
i
)
∈
D
A
s
∥
y
i
−
ψ
i
(
x
;
θ
)
∥
2
2
\theta_{s}=\arg \min _{\theta} \sum_{\left(x, \mathbf{y}_{i}\right) \in D_{A}^{s}}\left\|\mathbf{y}_{i}-\psi_{i}(x ; \theta)\right\|_{2}^{2} \tag{8}
θs=argθmin(x,yi)∈DAs∑∥yi−ψi(x;θ)∥22(8)
实现
Github: DeepPose implementation in Chainer
总结
通读下来,DeepPose有以下几大特点:
- 首次将DNN引入了关键点检测领域,为关键点检测提供了新的思路
- 将关键点定位问题建模为关键点的坐标值的回归问题
- 使用cascade的方式,逐阶段对预测进行refine操作,从而得到高精确度的预测结果
之所以能使用cascade的方式,逐阶段提高精度的原因在于,随着
s
s
s 的提高,模型需要回归的值的范围越来越小,回归所产生的绝对误差也越来越小,从而可以提高模型回归精度。但是多阶段的模型在预测阶段,难免可能存在误差积累的问题,关于这个问题,作者在文中并没有讨论。
近几年主流的关键点检测算法,基本都是基于上述3个方面进行的改进。从实验结果来看,DeepPose的检测精度并不是很高,但是作为一种创世纪般的算法,理解上述特点才是关键。同时,其采用的归一化坐标值的方式也值得注意一下。



























 1137
1137

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








