下面来谈谈这篇论文提出的新的解决机制:
分段机制:
该篇论文提出的第一个改进机制称为分段机制(PM),将
作为输入,并在
中输出扰动值
,其中:
的概率密度函数(pdf)是分段常数函数,如下所示:
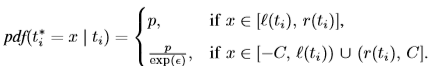
其中:

令为
的缩写。下图说明了
= 0,
= 0.5和
= 1情况下的
:
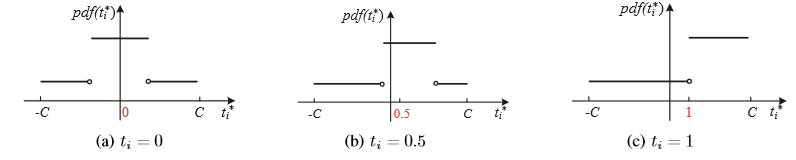
观察可知:
a. 当 = 0时,
是对称的并且由三“段”组成,其中中心段(即
[
])具有较高的概率(比其他两个要高);
b. 当从0增加到1时,中心部分的长度保持不变(因为
),但是最右边的部分的长度(即
)减小;
c. 当 = 1时,右边部分减小到0,
0的情况可以用类似的方式说明。
以下算法显示了PM的伪代码:

假设输入域是。通常,当输入域为
,
0时,用户使用PM计算
来扰动
,所以
,然后按照上述算法计算出
并将
提交给服务器,其中
表示算法输出的噪声值。可以证明
是
的无偏估计量。上述方法要求用户知道
值。
这种方法是先将原始输入域扰动至规定输入域,再将扰动系数和噪声值之积对外发布。
以下引理确保了上述算法理论的可行性:
引理1:该算法算法满足-本地差异隐私。另外,给定输入值,它会返回一个带有
=
(期望)的噪声值
,以及方差:
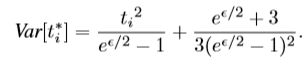
通过引理1,PM返回一个噪声值,其方差最大(即
= 1时)为:

下图中的紫色虚线说明了PM作为此函数的最坏情况方差:

通过观察可知:
a. 当 ≥ 1.29时,PM的最坏情况方差明显小于Duchi等人的解;
b. 当 < 1.29时,PM的最差方差仅略大于后者,其中1.29是Duchi等人解决方案和PM方案在
坐标上的交点。
可以证明,不管PM的值如何,PM的最坏方差都严格小于Laplace机制。与Laplace机制和Duchi等人的解决方案相比,PM是更可取的选择。
此外,引理1还表明PM中的随着
的减少而单调减少,这使得PM在输入数据的分布偏向小幅度值时特别有效。相反,Duchi等人的解决方案产生的噪声方差随
的减小而增加,见下方程:

现在来看被数据收集者用来推断所有的平均值的估计量
。该估计量的方差是
的平均方差的
。
基于此,以下引理建立了的精度保证:
引理2:令和
。 至少具有(1-β)概率,
 。(论文省略了证明)
。(论文省略了证明)
备注:
a. PM与在上一篇中描述的SCDF和Stairease mechanism具有某些相似之处,因为PM中的附加噪声也像SCDF和Stairease mechanism一样遵循分段恒定分布;
b. 另一方面,PM和SCDF/Stairease mechanism之间存在两个关键差异:
a) SCDF和Staircase机制假定无界输入,并因此产生无界输出(即范围为())。 相反,PM既有边界输入(
)又有边界输出(
);
b) SCDF/Stairease mechanism的噪声分布由无数个独立于数据的“段”组成,而PM的输出分布由三个“段”组成,其长度和位置取决于输入数据。
下一篇讲另一种改动机制。






















 1345
1345











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








