中心化、本地化差分隐私基础知识

差分隐私的背景和概念

由于互联网的发展，包括智能手机在内的各种终端数量剧烈的增长，使得各种公司和组织，以及政府需要收集和分析巨量的数据。在这个过程中，关于个人信息的隐私保护成为了一个大的问题。一些在大数据环境下的隐私保护方案，包括k-匿名技术，在需要发布用户数据的情况下，k-匿名可以较为有效地保护个人的隐私不被泄露。因为其可以保证具有相同敏感属性的等价类中，至少具有K个记录，这样攻击者便无法分辨某一用户具体是哪一条记录。然而，k-匿名还是无法阻止一些攻击，无法提供数学可证明的安全性。在同质攻击的场景下，由于k条记录中敏感值相同，无法阻止攻击者获取某用户的隐私信息。或者在攻击者已知某用户的一些背景的信息情况下，则其可以推断某用户的敏感信息。

而在差分隐私的场景下，任何一条信息的增减，都不会影响最终的查询结果，因此，对于攻击者具备的知识并不关心。差分隐私可以提供一种可证明的量化方法，来保护个人的隐私数据，同时向数据发布和分析者提供限制条件下相对准确的数据。一方面，差分隐私可以按照隐私预算向用户提供隐私保护性，但是根据差分隐私算法可证明的性质，又可以提供对应的数据可用性，这都是形式化可证明的。

差分隐私技术可以分为两类，在传统应用场景下，需要一个数据中心来收集和发布分析数据，称为中心化的差分隐私，而如果在本地处理隐私数据，则称为本地化的差分隐私。对于本地化的差分隐私，由于近年来各种终端设备的疯狂增长，和这些设备算力的提高，本地差分隐私成为了一个热门的方向。这也获得了一些实际的应用，例如在苹果设备和谷歌的浏览器上。

中心化差分隐私

理解差分隐私的一个点在于理解，差分隐私是通过向查询结果中添加一个随机噪声来保护隐私的，这个噪声是一个随机变量，服从某种分布。 这样子，攻击者只有在很多次查询数据的情况下，通过统计随机变量的分布，来推断隐私信息，但是实际上攻击者无法不受限制地去查询信息。实际上，查询信息需要消耗隐私预算，通过有限的隐私预算来阻止攻击者通过查询结果的概率分布来推断信息。

在不使用差分隐私的情况下，攻击者如何获取隐私信息呢？对于某一个数据集，攻击者先查询其统计量，例如未婚人群的个数，然后再查询某人的数据加入到这个数据集之后的统计量，此时，可以根据统计量的变化情况，来准确推断这个人的敏感信息。因此，可以看出，差分隐私中的“差分”，即为两个相邻的数据集的意味，而差分隐私就是要使得攻击者无法分辨这两个数据集，从而保护这两个数据之间的“差”的私密性，即某用户的数据。

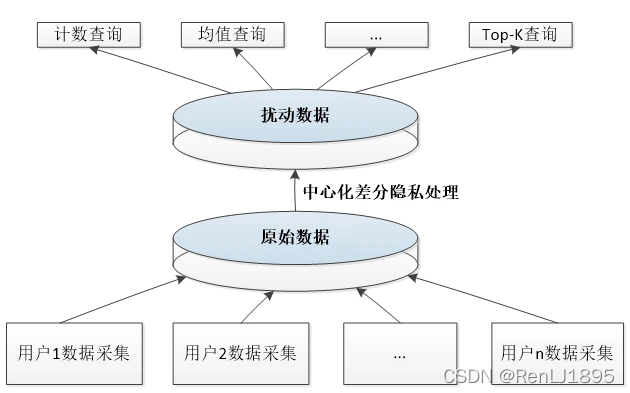
下面先看传统的中心化差分隐私，在这种情况下，中心化的数据收集者拥有一个集中管理的数据集，然后发布这个数据集的统计量，他需要完成其中的隐私保护工作。

$ϵ$-差分隐私

设$x$和$x^{\prime }$是两个相邻的数据集，即它们之间差了一条数据，设$\mathcal{M}:x\mapsto y$是随机化的机制，即查询结果为$y=\mathcal{M}(x)$，那么可以这样子表示两个查询结果之间的距离：

$$D_{\infty }=\underset{y}{\max }\ln \frac{Pr(\mathcal{M}(x)=y)}{Pr(\mathcal{M}(x^{\prime })=y)}\text{\hspace{1em}(1)}$$

这相当于对于某个输出，两个相邻数据集的查询结果为这个输出的最大概率差，实际上，这个式子可以认为是来源于KL散度的定义。如果令$D_{\infty }<ϵ$，再将上式通过指数运算消去，对于任意的输出集合$S$，则可以得到$ϵ$-隐私保护的定义：
$$Pr(\mathcal{M}(x)\in S)<e^{ϵ}Pr(\mathcal{M}(x^{\prime })\in S)\text{\hspace{1em}(2)}$$

这样子就可以更为方便地理解隐私保护的定义，对于松弛版本的$ϵ$隐私保护，其定义为：
$$Pr(\mathcal{M}(x)\in S)<e^{ϵ}Pr(\mathcal{M}(x^{\prime })\in S)-\delta \text{\hspace{1em}(3)}$$

同样可以通过变换理解为式(1)的情况：

$$D_{\infty }=$$