考研数二要掌握的高中知识点（三）

一、任意角

1. 任意角概念

初中学习了角的相关知识，角是由射线（即始边）围绕端点旋转而成，旋转后的边叫做终边。

初中阶段主要探讨的是 $360^{\circ }$ 内的角，高中阶段对角进行了进一步的学习，并且称其为任意角

1. 任意角

任意角分为：

• 正角：终边逆时针旋转的角叫做正角，角度用正数表示
• 零角：终边未旋转的角叫做零角
• 负角：终边顺时针旋转的角叫做负角，角度用负数表示
  
  

2. 任意角在平面直角坐标系上的表示

在平面直角坐标系中，角默认的形态：以坐标系的原点为端点， 原点右侧的 $x$ 轴为始边

3. 象限角

象限角是在平面直角坐标系中，根据终边所处的位置对角的叫法，当终边在第一象限内时，称为第一象限角。当终边在第二象限时，称为第二象限角。以此类推

如果终边正好与 $x$ 或 $y$ 轴重合，那么这个角就不属于任何象限，即不是象限角

4. 终边和角

一个角只有一个终边，但是一个终边可以有无数的个角，比如 $60^{\circ }$ 和 $420^{\circ }$ 的终边就相同，但这是两个不同的角

5. 终边相同的角

以一个角的终边为起点，只要旋转 $360^{\circ }$ 的整数倍，那么终边就还会回到原来的位置，这时候形成的新角，就是终边相同的角，所以：$\alpha +360^{\circ }\ast k，(k\in Z（k是旋转的圈数，是全体整数）)$，就全是终边相同的角

6. 已知 $\alpha$ 的象限，求 $\frac{\alpha }{n}$ 的象限

例，已知 $\alpha$ 在第一象限，求 $\frac{\alpha }{3}$ 的象限

步骤1：先画一个平面直角坐标系，并把每个象限都 $n$ 等分，题中是 $\frac{\alpha }{3}$，所以就在每个象限 $3$ 等分，这时平面直角坐标系会被分成 $16$ 份

步骤2：从第一象限靠近 $x$ 轴的那一份开始，逆时针标记序号，从 $1$ 开始标记到 $4$，然后再重新从 $1$ 开始，直到标记到第四象限靠近 $x$ 轴的那一份。以题目为例，记号按逆时针排列为：

• 第一象限：1、2、3
• 第二象限：4、1、2
• 第三象限：3、4、1
• 第四象限：2、3、4

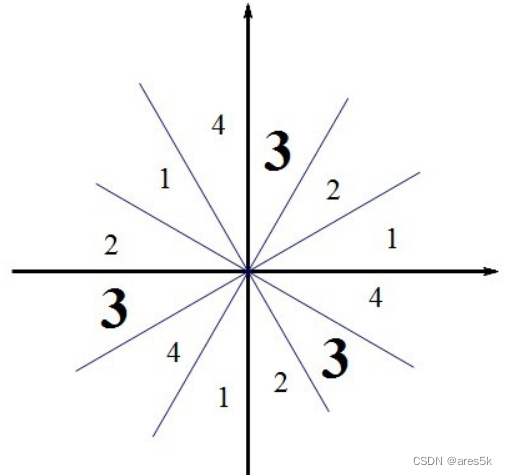
步骤3：已知的角是第几象限，就找到对应的序号，这个序号所在的象限就是 $\frac{\alpha }{3}$ 所处的象限，以题中为例，$\alpha$ 在第一象限，所以要找到所有序号是 $1$ 的象限，分别是：第一象限、第二象限、第三象限。所以 $\frac{\alpha }{3}$ 就处于第一象限、第二象限、第三象限。

2. 角度制与弧度制

1. 角度制与弧度制

在初中，角的单位是度（如：$360^{\circ }$），在高中，角有了新的单位，弧度制（$radian$），一般记做 $rad$（如：360 rad），但通常习惯将弧度制的单位省略（如：360）

2. 角度制与弧度制下，周角和角的大小

圆和圆中角的概念：

• 圆：射线旋转一周围城的图形
• 半径（$r$）：圆心到圆边的距离
• 角（$\alpha$）：半径旋转后，终边和始边的夹角
• 弧长（$l$）：半径旋转后，终边和始边在圆边移动的距离
• 周角：射线旋转一周的角
  
  

角度制下周角和角的大小

周角：被人为定义成 $360^{\circ }$

角的大小：周角和旋转比例的比值

例：在圆中，一个角旋转了 $\frac{1}{3}$，则这个角的大小就是 $\alpha =\frac{360^{\circ }}{3}=120^{\circ }$

弧度制下周角和角的大小

角的大小：弧长和半径的比值，即：$\alpha =\frac{l}{r}$

周角：仍然是弧长和半径的比值，只不过这个弧长是特殊的，是半径旋转一圈的弧长，也就是圆周长，即：$\alpha =\frac{2\pi r}{r}=2\pi$

3. 角度制与弧度制的换算

前面知道了，角度制下，周角是 $360^{\circ }$，弧度制下，周角是 $2\pi$，所以角度和弧度的周角等式为：$360^{\circ }=2\pi$，从而也可以得出：$\pi =180^{\circ }$，而角度制与弧度制的换算就是基于这个 $\pi =180^{\circ }$

例 1，把弧度制 $\frac{\pi }{3}$ 和 $\frac{11}{6}\pi$ 换成角度制：

解：

$\because \pi =180^{\circ }，\therefore \frac{\pi }{3}=\frac{180^{\circ }}{3}=60^{\circ }，\frac{11}{6}\pi =\frac{11}{6}\ast 180^{\circ }=330^{\circ }$

例 2，把角度制 $300^{\circ }$ 和 $70^{\circ }$ 换成弧度制：

$\because \pi =180^{\circ }，\therefore 300^{\circ }=300^{\circ }\ast \frac{\pi }{180^{\circ }}=\frac{5}{3}\pi ，70^{\circ }=70^{\circ }\ast \frac{\pi }{180^{\circ }}=\frac{7\pi }{18}$

3. 弧长公式和扇形面积公式

求解弧长和面积时，必须得先已知两个信息， 半径（$r$）和角的大小（$\alpha$），知道这两个信息后，还得根据角度制和弧度制来使用不同的公式来计算弧长和面积

1. 弧长公式

• 角度制：角度制中，周角和圆周长是等比例关系，即：$360^{\circ }=2\pi r$， 当已知一个角的大小后，那么就可以算出这个角和周角的比例，而弧长和圆周长的比例，应与其相同，所以弧长公式为：$\frac{360^{\circ }}{{\alpha }^{\circ }}=\frac{2\pi r}{l}$

• 弧度制：因为角大小的公式为：$\alpha =\frac{l}{r}$，所以弧长的公式就是：$l=\alpha \ast r$，需要注意的是如果 $\alpha$ 给的是角度制的单位时，应先将其换算成弧度制单位

2. 面积公式

• 角度制：角度制中，周角和圆的面积是等比例关系，即：$360^{\circ }=\pi r^2$， 当已知一个角的大小后，那么就可以算出这个角和周角的比例，而扇形面积和圆面积的比例，应与其相同，所以面积公式为：$\frac{360^{\circ }}{{\alpha }^{\circ }}=\frac{\pi r^2}{S}$

• 弧度制：弧度制其实和角度制同理，弧度制中，周角和圆的面积是等比例关系，即：$2\pi =\pi r^2$， 当已知一个角的大小后，那么就可以算出这个角和周角的比例，而扇形面积和圆面积的比例，应与其相同，所以面积公式为：$\frac{2\pi }{\alpha }=\frac{\pi r^2}{S}$，化简后为：$\frac{1}{2}\ast \alpha \ast r^2$，因为 $\frac{1}{2}\ast \alpha \ast r^2=\frac{1}{2}\ast \alpha \ast r\ast r$，所以也可以记为：$\frac{1}{2}\ast l\ast r$
  
  

例，一个扇形的半径是 $2$，角度是 $120^{\circ }$，求弧长和面积？

角度制，解：

弧长，$\because \frac{360^{\circ }}{{\alpha }^{\circ }}=\frac{2\pi r}{l}，\therefore \frac{360^{\circ }}{120^{\circ }}=\frac{4\pi }{l}，\therefore 弧长：\frac{4}{3}\pi$

面积，$\because \frac{360^{\circ }}{{\alpha }^{\circ }}=\frac{\pi r^2}{S}，\therefore \frac{360^{\circ }}{120^{\circ }}=\frac{4\pi }{S}，\therefore 面积：\frac{4}{3}\pi$

弧度制，解：

因为 $120^{\circ }$ 是角度制单位，需要先换算成弧度制，即：$120^{\circ }\ast \frac{\pi }{180^{\circ }}=\frac{2\pi }{3}$

弧长，$\because l=\alpha \ast r，\therefore l=\frac{2\pi }{3}\ast 2，\therefore 弧长：\frac{4}{3}\pi$

面积，$\because S=\frac{1}{2}\ast \alpha \ast r^2，\therefore S=\frac{1}{2}\ast \frac{2\pi }{3}\ast 4，\therefore 面积：\frac{4}{3}\pi$

二、三角函数

1. 三角函数的概念

在平面直角坐标系中，画一个角并在终边任取一点，然后做 $x$ 轴的垂线，这时就会围成一个三角形。在这个三角形中：

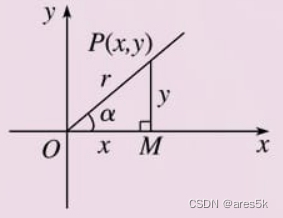
• 对边：垂线的那条边。它的高度与 $y$ 坐标值相同，一般记为 $y$
• 邻边：$x$ 轴的那条边。它的长度与 $x$ 坐标值相同，一般记为 $x$
• 斜边：一般记为 $r$，按照勾股定理，它的长度是，$r=\sqrt{x^2+y^2}$

高中阶段主要涉及的三角函数有：

• 正弦（sine）：$\sin \alpha =\frac{对边}{斜边}=\frac{y}{r}$，给定一个角，计算其对边和斜边的比值

• 余弦（cosine）：$\cos \alpha =\frac{邻边}{斜边}=\frac{x}{r}$，给定一个角，计算邻边和斜边的比值

• 正切（tangent）：$\tan \alpha =\frac{对边}{邻边}=\frac{y}{x}$，给定一个角，计算对边和邻边的比值
  
  

等腰直角三角形（$90^{\circ }$、$45^{\circ }$、$45^{\circ }$）和 直角三角形（$90^{\circ }$、$30^{\circ }$、$60^{\circ }$）必须背下来的三角函数值

因为等腰直角三角形（$90^{\circ }$、$45^{\circ }$、$45^{\circ }$）的两条直角边相等，所以设一条直角边是 $a$，则另一条直角边肯定也是 $a$，然后可以通过勾股定理算出第三条边是 $\sqrt{a^2+a^2}=\sqrt{2}a$，所以：

• $\sin 45^{\circ }=\frac{a}{\sqrt{2}a}=\frac{\sqrt{2}}{2}$

• $\cos 45^{\circ }=\frac{a}{\sqrt{2}a}=\frac{\sqrt{2}}{2}$

• $\tan 45^{\circ }=\frac{a}{a}=1$
  
  

因为直角三角形（$90^{\circ }$、$30^{\circ }$、$60^{\circ }$）中，$30^{\circ }$ 的对边是斜边的一半，所以设 $30^{\circ }$ 的对边是 $a$，则斜边就是 $2a$，然后可以通过勾股定理算出第三条边是 $x^2+a^2=(2a{)}^2$，即 $x=\sqrt{3}a$，所以：

• $\sin 30^{\circ }=\frac{a}{2a}=\frac{1}{2}$，$\cos 60^{\circ }=\frac{a}{2a}=\frac{1}{2}$

• $\cos 30^{\circ }=\frac{\sqrt{3}a}{2a}=\frac{\sqrt{3}}{2}$，$\sin 60^{\circ }=\frac{\sqrt{3}a}{2a}=\frac{\sqrt{3}}{2}$

• $\tan 30^{\circ }=\frac{a}{\sqrt{3}a}=\frac{\sqrt{3}}{3}$

• $\tan 60^{\circ }=\frac{\sqrt{3}a}{a}=\sqrt{3}$
  
  

特殊角度要背下来的三角函数值

三角函数名	$0^{\circ }$（弧度制：$0$）	$90^{\circ }$（弧度制：$\frac{\pi }{2}$）	$180^{\circ }$（弧度制：$\pi$）	$270^{\circ }$（弧度制：$\frac{3\pi }{2}$）	$360^{\circ }$（弧度制：$2\pi$）
$\sin$	$0$	$1$	$0$	$-1$	$0$
$\cos$	$1$	$0$	$-1$	$0$	$1$
$\tan$	$0$	没意义，不成立	$0$	没意义，不成立	$0$

2. 三角函数的的正负

先记住一点：斜边 $r$，永远是正数

1. $\sin$ 的正负

因为 $\sin \alpha =\frac{y}{r}$，又因为斜边 $r$ 永远是正数，所以 $\sin$ 的正负主要取决于 $y$，即：$y$ 是正数时 $\sin$ 就是正的，$y$ 是负数时 $\sin$ 就是负的。

从图像上来看，当角的终边在一、二象限时，$\sin$ 就是正的。终边在三、四象限时 $\sin$ 就是负的

2. $\cos$ 的正负

因为 $\cos \alpha =\frac{x}{r}$，又因为斜边 $r$ 永远是正数，所以 $\cos$ 的正负主要取决于 $x$，即：$x$ 是正数时 $\cos$ 就是正的，$x$ 是负数时 $\cos$ 就是负的。

从图像上来看，当角的终边在一、四象限时，$\cos$ 就是正的。终边在二、三象限时 $\cos$ 就是负的

3. $\tan$ 的正负

因为 $\tan \alpha =\frac{y}{x}$，所以 $y$ 和 $x$ 同号时 $\tan$ 就是正的， $y$ 和 $x$ 异号时 $\tan$ 就是负的，

从图像上来看，当角的终边在一、三象限时，$\cos$ 就是正的。终边在二、四象限时 $\cos$ 就是负的

三角函数正负的图像口诀

一全正，二正弦，三正切，四余弦

一全正：终边在第一象限时，$\sin$、$\cos$、$\tan$ 都是正的

二正弦：终边在第二象限时，$\sin$ 是正的，$\cos$、$\tan$ 是负的

三正切：终边在第三象限时，$\tan$ 是正的，$\sin$、$\cos$ 是负的

四余弦：终边在第四象限时，$\cos$ 是正的，$\sin$、$\tan$ 是负的

3. 同角三角函数的关系式

在同一角内，只要知道 $\sin 、\cos 、\tan$ 中的任意一个，就可以通过下面两个公式计算出另外两个三角函数

1. ${\sin }^2\alpha +{\cos }^2\alpha =1$

公式原理推导：

$\because$ 在直角坐标系中，角的三边分别为：对边 $y$、邻边 $x$，斜边 $r$

$\therefore$ 通过勾股定理，可以得出斜边 $r=\sqrt{y^2+x^2}$

$\because$ $\sin \alpha =\frac{y}{r}$，$\cos \alpha =\frac{x}{r}$

$\therefore$ $\sin \alpha =\frac{y}{\sqrt{y^2+x^2}}$，$\cos \alpha =\frac{x}{\sqrt{y^2+x^2}}$

$\therefore {\sin }^2\alpha +{\cos }^2\alpha =(\frac{y}{\sqrt{y^2+x^2}}{)}^2+(\frac{x}{\sqrt{y^2+x^2}}{)}^2=\frac{y^2}{y^2+x^2}+\frac{x^2}{y^2+x^2}=\frac{y^2+x^2}{y^2+x^2}=1$

2. $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$

公式原理推导：

$\because$ $\sin \alpha =\frac{y}{r}$，$\cos \alpha =\frac{x}{r}$

$\therefore \frac{\sin \alpha }{\cos \alpha }=\frac{y}{r}\ast \frac{r}{x}=\frac{y}{x}$

$\because$ $tan=\frac{y}{x}$，$\therefore \tan \alpha =\frac{\sin \alpha }{\cos \alpha }$

例：已知 $\sin \alpha +\cos \alpha =\frac{1}{5}$，求 $\sin \alpha \ast \cos \alpha$ 的值

解：

已知 $\sin \alpha +\cos \alpha =\frac{1}{5}$，又已知 ${\sin }^2\alpha +{\cos }^2\alpha =1$，这时就得到了一个关于 $\sin \alpha 和\cos \alpha$ 的方程组，只要将方程组解开，分别求出 $\sin \alpha 和\cos \alpha$，再将其代入到 $\sin \alpha \ast \cos \alpha$ 中就可以

方程组：$\{\begin{array}{l}\sin \alpha +\cos \alpha =\frac{1}{5}\\ {\sin }^2\alpha +{\cos }^2\alpha =1\end{array}$

$\because \sin \alpha +\cos \alpha =\frac{1}{5}$

$\therefore \cos \alpha =\frac{1}{5}-\sin \alpha$，并将其代入到 ${\sin }^2\alpha +{\cos }^2\alpha =1$，代入后为：${\sin }^2\alpha +(\frac{1}{5}-\sin \alpha {)}^2=1$

解得：$\sin \alpha =\frac{4}{5}$ 或 $\sin \alpha =-\frac{3}{5}$，然后分别代入到 $\sin \alpha +\cos \alpha =\frac{1}{5}$ 中

解得：$\sin \alpha =\frac{4}{5}$ 时 $\cos \alpha =-\frac{3}{5}$，$\sin \alpha =-\frac{3}{5}$ 时 $\cos \alpha =\frac{4}{5}$

$\sin \alpha \ast \cos \alpha =-\frac{3}{5}\ast \frac{4}{5}=-\frac{12}{25}$

上题中，虽然使用方程组可以求解，但计算过程却很耗时。其实已知 $\sin \alpha +\cos \alpha$ 或 $\sin \alpha -\cos \alpha$ 或 $\sin \alpha \ast \cos \alpha$ 中的任意一个，就可以利用完全平方公式求出另外两个的值

现在利用完全平方公式，对刚才的题重新求解，已知 $\sin \alpha +\cos \alpha =\frac{1}{5}$，求 $\sin \alpha \ast \cos \alpha$ 的值：

解：

让等号两边同时乘方，凑成完全平方公式：$(\sin \alpha +\cos \alpha {)}^2=\frac{1}{25}$

将完全平方公式展开：${\sin }^2\alpha +{\cos }^2\alpha +2\ast \sin \alpha \ast \cos \alpha =\frac{1}{25}$

$\because {\sin }^2\alpha +{\cos }^2\alpha =1$

$\therefore 1+2\ast \sin \alpha \ast \cos \alpha =\frac{1}{25}$

$\therefore 2\ast \sin \alpha \ast \cos \alpha =\frac{1}{25}-1$

$\therefore \sin \alpha \ast \cos \alpha =-\frac{12}{25}$

趁热打铁，再来一道题，$\sin \alpha +\cos \alpha =\frac{\sqrt{5}}{2}$，则 $\sin \alpha -\cos \alpha =$ ?

这道题用方程组的方式仍然可以求解，但是这里还是使用更简单的完全平方公式的方式

解：

让等号两边同时乘方，凑成完全平方公式：$(\sin \alpha +\cos \alpha {)}^2=\frac{5}{4}$

将完全平方公式展开：${\sin }^2\alpha +{\cos }^2\alpha +2\ast \sin \alpha \ast \cos \alpha =\frac{5}{4}$

$\because {\sin }^2\alpha +{\cos }^2\alpha =1$

$\therefore 1+2\ast \sin \alpha \ast \cos \alpha =\frac{5}{4}$

$\therefore 2\ast \sin \alpha \ast \cos \alpha =\frac{1}{4}$

这个方程暂时解到这里就可以了，现在把 $\sin \alpha -\cos \alpha$ 也变成完全平方公式的样子：

$(\sin \alpha -\cos \alpha {)}^2={\sin }^2\alpha +{\cos }^2\alpha -2\ast \sin \alpha \ast \cos \alpha$

$\because {\sin }^2\alpha +{\cos }^2\alpha =1$，又 $\because 2\ast \sin \alpha \ast \cos \alpha =\frac{1}{4}$

$\therefore (\sin \alpha -\cos \alpha {)}^2=1-\frac{1}{4}$

$\therefore (\sin \alpha -\cos \alpha {)}^2=\frac{3}{4}$

$\therefore \sin \alpha -\cos \alpha =\frac{\sqrt{3}}{2}$

4. 诱导公式

1. 诱导公式的概念

$30^{\circ }$、$45^{\circ }$、$60^{\circ }$、$90^{\circ }$、$180^{\circ }$、$360^{\circ }$ 的角具有特殊性，它们对应的三角函数值前面已经背过，所以当角度是这些时，就可以很快的知道三角函数 $\sin$、$\cos$、$\tan$ 的值。

诱导公式：将一个大的角变成小角（最好能变成上述那些小角），从而能快速得到三角函数值。

例：计算 $\sin 390^{\circ }$ 的函数值？

这个时候很难直接计算，可以先将其拆解为：$\sin (360^{\circ }+30^{\circ })$，又因为终边相同的角的同一三角函数的值相等的特点，所以 $360^{\circ }$ 的整数倍都可以忽略，所以只需要计算 $\sin 30^{\circ }$ 就可以，即：$\sin 390^{\circ }=\sin (360^{\circ }+30^{\circ })=\sin 30^{\circ }=\frac{1}{2}$

前面例子， $\sin (360^{\circ }+30^{\circ })=\sin 30^{\circ }$，其实就无形中使用了 $\sin (k\ast 2\pi +\alpha )=\sin \alpha$ 这个诱导公式。但并不是所有大角化小角的问题都可以使用这个公式。根据将原角拆分的粒度不同，有很多对应的诱导公式，刚刚这个只合适将角拆分成 $360^{\circ }$ 的整数倍时使用。

2. 常见的诱导公式结构，要背下来

为了方便理解，建议将诱导公式中的 $\alpha$ 全部当做锐角

(1) 关于 $-\alpha$ 的诱导公式：

① $\sin (-\alpha )=-\sin \alpha$

② $\cos (-\alpha )=\cos \alpha$

③ $\tan (-\alpha )=-\tan \alpha$

证明：假设 $\alpha$ 为锐角，可在其终边取点坐标 $P(x,y)$，而 $-\alpha$ 与 $\alpha$ 的终边关于 $x$ 轴对称，所以 $-\alpha$ 对应的点坐标为 $P(x,-y)$

即：$\sin (-\alpha )=\frac{-y}{r}$，$\sin (\alpha )=\frac{y}{r}$，所以 $\sin (-\alpha )=-\sin \alpha$

即：$\cos (-\alpha )=\frac{x}{r}$，$\cos (\alpha )=\frac{x}{r}$，所以 $\cos (-\alpha )=\cos \alpha$

即：$\tan (-\alpha )=\frac{-y}{x}$，$\tan (\alpha )=\frac{y}{x}$，所以 $\tan (-\alpha )=-\tan \alpha$

(2) 关于 $\frac{\pi }{2}+\alpha$ 的诱导公式：

① $\sin (\frac{\pi }{2}+\alpha )=\cos \alpha$

② $\cos (\frac{\pi }{2}+\alpha )=-\sin \alpha$

③ $\tan (\frac{\pi }{2}+\alpha )=-\frac{1}{\tan \alpha }$

证明：假设 $\alpha$ 为锐角，可在其终边取点坐标 $P(x,y)$，然后在 $\frac{\pi }{2}+\alpha$ 的终边取点坐标 $P(-y,x)$，这时从两个终边的点坐标分别向 $x$ 轴做垂线，围成的两个三角形是全等关系

即：$\sin (\frac{\pi }{2}+\alpha )=\frac{x}{r}$，$\cos (\alpha )=\frac{x}{r}$，所以 $\sin (\frac{\pi }{2}+\alpha )=\cos \alpha$

即：$\cos (\frac{\pi }{2}+\alpha )=\frac{-y}{r}$，$\sin (\alpha )=\frac{y}{r}$，所以 $\cos (\frac{\pi }{2}+\alpha )=-\sin \alpha$

即：$\tan (\frac{\pi }{2}+\alpha )=\frac{x}{-y}$，$\cos (\alpha )=\frac{y}{x}$，所以 $\tan (\frac{\pi }{2}+\alpha )=-\frac{1}{\tan \alpha }$

(3) 关于 $\frac{\pi }{2}-\alpha$ 的诱导公式：

① $\sin (\frac{\pi }{2}-\alpha )=\cos \alpha$

② $\cos (\frac{\pi }{2}-\alpha )=\sin \alpha$

③ $\tan (\frac{\pi }{2}-\alpha )=\frac{1}{\tan \alpha }$

证明：假设 $\alpha$ 为锐角，可在其终边取点坐标 $P(x,y)$，然后在 $\frac{\pi }{2}-\alpha$ 的终边取点坐标 $P(y,x)$，这时从两个终边的点坐标分别向 $x$ 轴做垂线，围成的两个三角形是全等关系

即：$\sin (\frac{\pi }{2}-\alpha )=\frac{x}{r}$，$\cos (\alpha )=\frac{x}{r}$，所以 $\sin (\frac{\pi }{2}-\alpha )=\cos \alpha$

即：$\cos (\frac{\pi }{2}-\alpha )=\frac{y}{r}$，$\sin (\alpha )=\frac{y}{r}$，所以 $\cos (\frac{\pi }{2}-\alpha )=\sin \alpha$

即：$\tan (\frac{\pi }{2}+\alpha )=\frac{x}{y}$，$\cos (\alpha )=\frac{y}{x}$，所以 $\tan (\frac{\pi }{2}-\alpha )=\frac{1}{\tan \alpha }$

(4) 关于 $\pi +\alpha$ 的诱导公式：

① $\sin (\pi +\alpha )=-\sin \alpha$

② $\cos (\pi +\alpha )=-\cos \alpha$

③ $\tan (\pi +\alpha )=\tan \alpha$

证明：假设 $\alpha$ 为锐角，可在其终边取点坐标 $P(x,y)$，而 $\pi +\alpha$ 与 $\alpha$ 的终边关于原点对称，所以 $-\alpha$ 对应的点坐标为 $P(-x,-y)$

即：$\sin (\pi +\alpha )=\frac{-y}{r}$，$\sin (\alpha )=\frac{y}{r}$，所以 $\sin (\pi +\alpha )=-\sin \alpha$

即：$\cos (\pi +\alpha )=\frac{-x}{r}$，$\sin (\alpha )=\frac{x}{r}$，所以 $\cos (\pi +\alpha )=-\cos \alpha$

即：$\tan (\pi +\alpha )=\frac{-y}{-x}$，$\sin (\alpha )=\frac{y}{x}$，所以 $\tan (\pi +\alpha )=\tan \alpha$

(5) 关于 $\pi -\alpha$ 的诱导公式：

① $\sin (\pi -\alpha )=\sin \alpha$

② $\cos (\pi -\alpha )=-\cos \alpha$

③ $\tan (\pi -\alpha )=-\tan \alpha$

证明：假设 $\alpha$ 为锐角，可在其终边取点坐标 $P(x,y)$，而 $\pi -\alpha$ 与 $\alpha$ 的终边关于 $y$ 轴对称，所以 $-\alpha$ 对应的点坐标为 $P(-x,y)$

即：$\sin (\pi -\alpha )=\frac{y}{r}$，$\sin (\alpha )=\frac{y}{r}$，所以 $\sin (\pi -\alpha )=\sin \alpha$

即：$\cos (\pi -\alpha )=\frac{-x}{r}$，$\cos (\alpha )=\frac{x}{r}$，所以 $\cos (\pi -\alpha )=-\cos \alpha$

即：$\tan (\pi -\alpha )=\frac{y}{-x}$，$\tan (\alpha )=\frac{y}{x}$，所以 $\tan (\pi -\alpha )=-\tan \alpha$

(6) 关于 $2\pi +\alpha$ 的诱导公式：

① $\sin (k\ast 2\pi +\alpha )=\sin \alpha$

② $\cos (k\ast 2\pi +\alpha )=\cos \alpha$

③ $\tan (k\ast 2\pi +\alpha )=\tan \alpha$

证明：因为 $2\pi =360^{\circ }$，而 $\alpha$ 的所有 $360^{\circ }$ 的整数倍都与其终边相等

即：$\sin (k\ast 2\pi +\alpha )=\sin \alpha$

即：$\cos (k\ast 2\pi +\alpha )=\cos \alpha$

即：$\tan (k\ast 2\pi +\alpha )=\tan \alpha$

3. 通过规律记忆诱导公式

诱导公式的规律：

• 将原式的角变为 $k\ast \frac{\pi }{2}+\alpha$ 的结构，$\alpha$ 就是我们要留下的小角

• 奇变偶不变

• 符号看象限

现在就以 $\sin 100^{\circ }$ 当做例子，演示当忘记诱导公式时，如何通过规律来完成同样的效果

(1) 将原式的角变为 $k\ast \frac{\pi }{2}+\alpha$ 的结构，$\alpha$ 就是我们要留下的小角

$\sin 100^{\circ }$，可以拆解成 $90^{\circ }+10^{\circ }$，换算成弧度制为： $1\ast \frac{\pi }{2}+\frac{\pi }{18}$，刚好可以满足所需的结构，然后留下小角 $\alpha$， 即在这一步得到了： $\sin \frac{\pi }{18}$

(2) 奇变偶不变

在 $k\ast \frac{\pi }{2}+\alpha$ 这个结构中，当 $k$ 是奇数时三角函数名需要变，是偶数时三角函数名不用变，即：

• 奇数时：$\sin \alpha \to \cos \alpha$，$\cos \alpha \to \sin \alpha$，$\tan \alpha \to \frac{1}{\tan \alpha }$

• 偶数时：$\sin \alpha$，$\cos \alpha$，$\tan \alpha$ 保持不变

上一步将 $\sin 100^{\circ }$ 拆解成 $k\ast \frac{\pi }{2}+\alpha$ 的结构，即：$1\ast \frac{\pi }{2}+\frac{\pi }{18}$，$k$ 是奇数 $1$，所以要把函数名变成 $\cos$，上一步最后的结果是 $\sin \frac{\pi }{18}$，所以这一步变换函数名后为：$\cos \frac{\pi }{18}$

(3) 符号看象限

指最终结果的符号，根据原三角函数的所在象限判断正负，原三角函数的值是正，结果就是正、原三角函数的值是负，结果就是负。其实判断象限只要利用三角函数正负的图像口诀就可以（一全正，二正弦，三正切，四余弦）

因为是根据原式判断，原式是 $\sin 100^{\circ }$，属于第二象限，而 $\sin$ 在第二象限是正的，所以结果就是正的，即在这一步得到了最终结果：$\cos \frac{\pi }{18}$，转换成角度制就是：$\cos 10^{\circ }$。

假设原式属于第三象限，则 $\sin$ 在第三象限是负的，结果就是 $-\cos \frac{\pi }{18}$

4. 碰见大角问题时的做题步骤

分三步：

1. 负化正：当题中的角是负数时，要先通过 $-\alpha$ 的诱导公式，将其变为关于 $\alpha$ 的三角函数
2. 大化小：尝试从大角中拆分出 $360^{\circ }$ 的整数倍，因为角的 $360^{\circ }$ 的整数倍的终边相同，所以可以直接舍弃
3. 小化锐：尝试从上一步的角中再拆分出 $180^{\circ }$、$90^{\circ }$，以便满足诱导公式中常见的 $\pi \pm \alpha$、$\frac{\pi }{2}\pm \alpha$
   
   

例：求 $\sin (-1320^{\circ })$

解：

第一步，负化正：因为角是负的，所以要先通过 $-\alpha$ 的诱导公式，$\sin (-\alpha )=-\sin \alpha$，将其变为关于 $\alpha$ 的三角函数，即：$-\sin 1320^{\circ }$

第二步，大化小：因为 $1320^{\circ }$ 中包含 $3$ 个 $360^{\circ }$，所以可以将其缩小为：$1320^{\circ }-360^{\circ }\ast 3=240^{\circ }$

第三步，小化锐：上一步 $240^{\circ }$ 又可以拆成 $180^{\circ }+60^{\circ }$，此时 $\alpha =60^{\circ }$ 已经变成锐角了，所以不用再拆分了。然后观察 $180^{\circ }+60^{\circ }$ ，可以发现其满足 $\sin (\pi +\alpha )$ 的结构，所以这里使用诱导公式 $\sin (\pi +\alpha )=-\sin \alpha$，即最终结果为：$-\sin 60^{\circ }=-\frac{\sqrt{3}}{2}$

三、正余弦的图像性质

1. 正余弦函数的定义域、值域和五点法画图

1. 五点法画图

只要会画正余弦函数图像，正余弦的图像性质就不需要背诵，每次都可以通过画图去理解。

通过五点法画出的正弦函数图像如下：

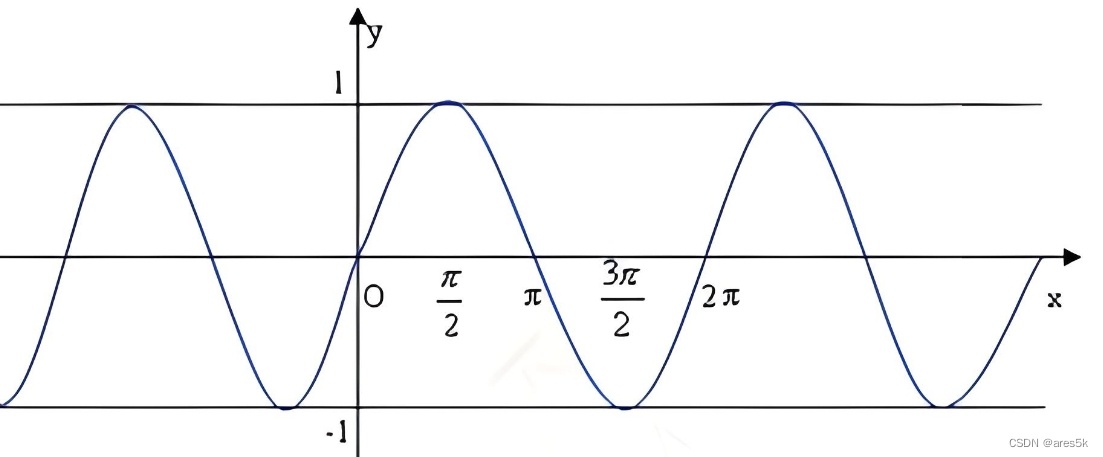
通过五点法画出的余弦函数图像如下：

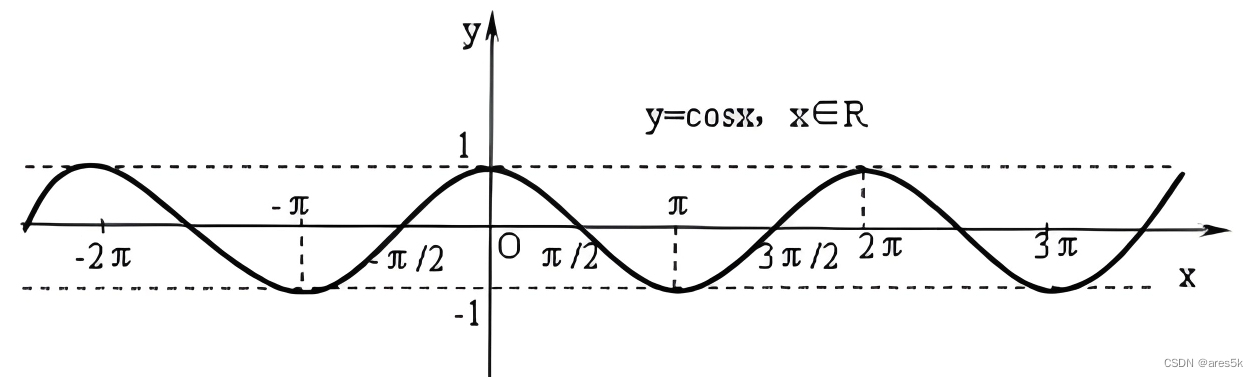
五点法：画正余弦函数图像时，分别对三角函数的参数取五个点即可。需要注意：三角函数的参数必须是弧度制

五个点分别是：$0$、$\frac{\pi }{2}$、$\pi$、$\frac{3\pi }{2}$、$2\pi$，因为这五个点的正余弦值是固定的，如下：

三角函数名	$0$	$\frac{\pi }{2}$	$\pi$	$\frac{3\pi }{2}$	$2\pi$
$\sin$	$0$	$1$	$0$	$-1$	$0$
$\cos$	$1$	$0$	$-1$	$0$	$1$

取点时要注意，并不只是让定义域 $x$ 满足这五个点，而是整个三角函数的参数

例：画出 $f(x)=\frac{1}{2}\sin (x-\frac{\pi }{6})$ 的大致图像

解：

因为 $\sin 的参数是(x-\frac{\pi }{6})$，所以要让 $(x-\frac{\pi }{6})$ 分别满足五个点：

第一点 $\sin 0$：自变量为 $x-\frac{\pi }{6}=0$ 的解，即：$x=\frac{\pi }{6}$，值为：$\frac{1}{2}\ast \sin 0=0$

第二点 $\sin \frac{\pi }{2}$：自变量为 $x-\frac{\pi }{6}=\frac{\pi }{2}$ 的解，即：$x=\frac{2\pi }{3}$，值为：$\frac{1}{2}\ast \sin \frac{\pi }{2}=\frac{1}{2}$

第三点 $\sin \pi$：自变量为 $x-\frac{\pi }{6}=\pi$的解，即：$x=\frac{7\pi }{6}$，值为：$\frac{1}{2}\ast \sin \pi =0$

第四点 $\sin \frac{3\pi }{2}$：自变量为 $x-\frac{\pi }{6}=\frac{3\pi }{2}$ 的解，即：$x=\frac{5\pi }{3}$，值为：$\frac{1}{2}\ast \sin \frac{3\pi }{2}=-\frac{1}{2}$

第五点 $\sin 2\pi$：自变量为 $x-\frac{\pi }{6}=2\pi$ 的解，即：$x=\frac{13\pi }{6}$，值为：$\frac{1}{2}\ast \sin 2\pi =0$

至此，已经知道了五个点对应的自变量和值了，所以就可以画出函数图像了

2. 定义域和值域

正弦函数在标准情况下，即：$f(x)=\sin x$ 时，定义域：$R$，值域：$[-1,1]$

正弦函数在复杂情况下，即：$f(x)=A\sin (\omega x+\phi )$ 时，值域：$[-A,A]$

余弦函数在标准情况下，即：$f(x)=\cos x$ 时，定义域：$R$，值域：$[-1,1]$

余弦函数在复杂情况下，即：$f(x)=A\cos (\omega x+\phi )$ 时，值域：$[-1,1]$

2. 正余弦函数的周期性

通过正余弦的标准函数图像可以看出，它们的最小正周期都是：$2\pi$

当复杂函数解析式时，周期计算也很简单，正余弦公式相同：$T=\frac{2\pi }{\omega }$，其中 $\omega$ 指定义域的系数

例：

$f(x)=\sin 3x$ 的周期为：$\frac{2\pi }{3}$

$f(x)=\sin (4x-\frac{\pi }{6})$ 的周期为：$\frac{2\pi }{4}=\frac{\pi }{2}$

3. 正余弦函数的奇偶性

1. 标准情况

正弦函数：通过标准的正弦图像可以看出，其基于原点对称，所以标准的正弦函数为奇函数

余弦函数：通过标准的余弦图像可以看出，其基于 $y$ 轴对称，所以标准的余弦函数为偶函数

2. 解析式为复杂情况时

当解析式比较复杂时，可以利用奇变偶不变的理论来分析它们的奇偶性：

正弦 $A\sin (\omega x+\phi )$：

• 当 $\phi$ 是 $\frac{\pi }{2}$ 的偶数倍时，正弦函数是奇函数
• 当 $\phi$ 是 $\frac{\pi }{2}$ 的奇数倍时，正弦函数是偶函数（因为奇变，所以要变成 $\cos$，从而成为偶函数）
  
  

余弦 $A\cos (\omega x+\phi )$：

• 当 $\phi$ 是 $\frac{\pi }{2}$ 的偶数倍时，余弦函数是偶函数
• 当 $\phi$ 是 $\frac{\pi }{2}$ 的奇数倍时，余弦函数是奇函数（因为奇变，所以要变成 $\sin$，从而成为奇函数）
  
  

当正弦、余弦中的 $\phi$ 不是 $\frac{\pi }{2}$ 的倍数时，那这个函数就是非奇非偶函数

4. 正余弦函数的对称性

1. 标准情况

正弦函数

对称轴：正弦函数在每个周期内都有两个对称轴，一个处于波峰处，一个处于波谷处，所以从标准正弦函数图像中可以看出，在一个周期内对称轴为：$\frac{\pi }{2}、\frac{3\pi }{2}$，按照这个规律，当函数图像是多个周期时，对称轴公式为：$\frac{\pi }{2}+k\pi$

对称中心：正弦函数图像中所有与 $x$ 轴的交点都是对称中心，所以从标准正弦函数图像中可以看出，一个周期内的对称中心分别有：$(0,0)、(\pi ,0)、(2\pi ,0)$，按照这个规律，当函数图像是多个周期时，对称中心公式为：$(k\pi ,0)$

余弦函数

对称轴：余弦函数在每个周期内也有两个对称轴，也是一个处于波峰处，一个处于波谷处，所以从标准余弦函数图像中可以看出，在一个周期内对称轴为：$\pi 、2\pi$，按照这个规律，当函数图像是多个周期时，对称轴公式为：$k\pi$

对称中心：余弦函数图像中所有与 $x$ 轴的交点都是对称中心，所以从标准余弦函数图像中可以看出，一个周期内的对称中心分别是：$\frac{\pi }{2}、\frac{3\pi }{2}$，按照这个规律，当函数图像是多个周期时，对称中心公式为：$(\frac{\pi }{2}+k\pi ,0)$

2. 解析式为复杂情况时

通过五点法画函数图像时可以总结到一个规律，不管三角函数的参数多么复杂，最终都会让其满足那五个点，这就代表不管三角函数参数多么复杂，正弦和余弦函数图像的曲线比例是不变的。这也就代表不管三角函数参数多么复杂，对称轴也好，对称中心也好，仍然会满足标准函数的比例。

一个标准的正弦函数 $\sin x$，当参数是 $x$ 时，其对称轴为：$\frac{\pi }{2}+k\pi$，即：对称轴的 $x$ 点为 $x=\frac{\pi }{2}+k\pi$，假设有一个复杂的正弦函数 $A\sin (\omega x+\phi )$，按照上面比例不变的观点，那么它的对称轴也应该是 $\frac{\pi }{2}+k\pi$，即：$(\omega x+\phi )=\frac{\pi }{2}+k\pi$，即，对称轴的 $x$ 点为 $x=\frac{\frac{\pi }{2}+k\pi +\phi }{\omega }$

正弦和余弦复杂函数的对称轴和对称中心都是这个道理，比例是不变的。

还有一种复杂函数 $A\sin (\omega x+\phi )\pm b$，这里 $\pm b$ 只会让函数图像上下移动，所以对称轴是不会受影响的，但是会影响对称中心，所以对称中心需要在标准的结果上 $\pm b$

例 1： 求函数 $f(x)=3\cos (2x+\frac{\pi }{3})+1$ 的对称轴？

解：

思路1：因为要求对称轴，所以末尾的 $+1$ 不用管

思路2：余弦函数的标准对称轴是 $k\pi$，所以只要让 $2x+\frac{\pi }{3}=k\pi$ 即可

结果：最后解得对称轴的定义域为：$x=\frac{k\pi }{2}-\frac{\pi }{6}$

例 2： 求函数 $f(x)=3\sin (3x-\frac{\pi }{4})-5$ 的对称中心？

解：

思路1：因为要求对称中心，所以末尾的 $-5$， 最后不能忘记

思路2：正弦函数的标准对称中心是 $(k\pi ,0)$，所以只要让 $(3x-\frac{\pi }{4})=k\pi$ 即可

结果：最后解得对称中心的定义域为：$x=\frac{k\pi }{3}+\frac{\pi }{12}$，正常对称中心的 $y$ 轴值为 $0$，但是这里要把末尾的 $-5$ 算上，即中心对称点为：$[(\frac{k\pi }{3}+\frac{\pi }{12}),-5]$

5. 正余弦函数的单调性

1. 标准情况

标准的正弦函数，在 $[-\frac{\pi }{2}+2k\pi ,\frac{\pi }{2}+2k\pi ]$ 区间内递增，在 $[\frac{\pi }{2}+2k\pi ,\frac{3\pi }{2}+2k\pi ]$ 区间内递减

标准的余弦函数，在 $[-\pi +2k\pi ,2k\pi ]$ 区间内递增，在 $[2k\pi ,\pi +2k\pi ]$ 区间内递减

2. 解析式为复杂情况时

上一章节记载了，不管三角函数的参数多么复杂，其函数图像比例不变，从而对称性和对称中心不变。单调性也是相同的的理论

以正弦函数举例，标准正弦函数的递增区间是 $[-\frac{\pi }{2}+2k\pi ,\frac{\pi }{2}+2k\pi ]$，即：$-\frac{\pi }{2}+2k\pi \le x\le \frac{\pi }{2}+2k\pi$，假设有一个复杂的正弦函数 $A\sin (\omega x+\phi )$，此时如果依然按照前面直接等量替换的做法，它的单调递增区间应该是 $-\frac{\pi }{2}+2k\pi \le (\omega x+\phi )\le \frac{\pi }{2}+2k\pi$，即：$\frac{-\frac{\pi }{2}+2k\pi -\phi }{\omega }\le x\le \frac{\frac{\pi }{2}+2k\pi -\phi }{\omega }$，其实这个结果不一定是准确的

等量替换这个思路是正确的，但是在等量替换之前，有一个非常重要的步骤一定要做，就是考虑跟谁等量替换

其实一个复杂的三角函数 $\sin (\omega x+\phi )$ ，可以看作成一个复合函数 $\{\begin{array}{l}f(t)=\sin t\\ t(x)=\omega x+\phi \end{array}$，而复合函数的单调性就涉及到同增异减的知识点了，所以想求 $\sin (\omega x+\phi )$ 的单调性，那就得先确定 $t(x)$ 是增函数还是减函数

求复杂三角函数的单调性的具体思路如下：

1. 求 $\sin (\omega x+\phi )$ 的单调递增区间：

• 当 $t(x)$ 是增函数时，根据同增异减，所以就用标准正弦函数的增区间进行等量替换
• 当 $t(x)$ 是减函数时，根据同增异减，所以就用标准正弦函数的减区间进行等量替换

2. 求 $\sin (\omega x+\phi )$ 的单调递减区间：

• 当 $t(x)$ 是增函数时，根据同增异减，所以就用标准正弦函数的减区间进行等量替换
• 当 $t(x)$ 是减函数时，根据同增异减，所以就用标准正弦函数的增区间进行等量替换
  
  

例 1：函数 $f(x)=3\sin (2x-\frac{\pi }{3})$ 的单调区间是？

解：

思路1：因为求的是单调区间，所以系数 $3$ 并不影响定义域，只需要关注 $\sin (2x-\frac{\pi }{3})$ 即可

思路2：因为 $\sin (2x-\frac{\pi }{3})$ 是一个复杂正弦函数，所以将其看成一个复合函数 $\{\begin{array}{l}f(t)=\sin t\\ t(x)=2x-\frac{\pi }{3}\end{array}$

思路3：因为 $2x-\frac{\pi }{3}$ 是一个 $x$ 系数大于 $0$ 的一次函数，所以 $t(x)$ 是单调递增函数

思路4：先求 $f(x)=3\sin (2x-\frac{\pi }{3})$ 的递增区间，因为 $t(x)$ 是增函数，按照同增递减理论，$2x-\frac{\pi }{3}$ 的增区间应该等于标准正弦函数的增区间，即：$-\frac{\pi }{2}+2k\pi \le (2x-\frac{\pi }{3})\le \frac{\pi }{2}+2k\pi$，解后得：$k\pi -\frac{\pi }{12}\le x\le k\pi +\frac{5\pi }{3}$，整理后为：$[k\pi -\frac{\pi }{12},k\pi +\frac{5\pi }{3}]$

思路5：再求 $f(x)=3\sin (2x-\frac{\pi }{3})$ 的递减区间，因为 $t(x)$ 是增函数，按照同增递减理论，$2x-\frac{\pi }{3}$ 的减区间应该等于标准正弦函数的减区间，即：$\frac{\pi }{2}+2k\pi \le (2x-\frac{\pi }{3})\le \frac{3\pi }{2}+2k\pi$，关于 $x$ 的不等式就不算了，太麻烦了。

例 2：函数 $f(x)=3\sin (\frac{\pi }{3}-2x)$ 的单调区间是？

思路1：因为求的是单调区间，所以系数 $3$ 并不影响定义域，只需要关注 $\sin (\frac{\pi }{3}-2x)$ 即可

思路2：因为 $\sin (\frac{\pi }{3}-2x)$ 是一个复杂正弦函数，所以将其看成一个复合函数 $\{\begin{array}{l}f(t)=\sin t\\ t(x)=\frac{\pi }{3}-2x\end{array}$

思路3：因为 $\frac{\pi }{3}-2x$ 是一个 $x$ 系数小于 $0$ 的一次函数，所以 $t(x)$ 是单调递减函数

思路4：先求 $f(x)=3\sin (\frac{\pi }{3}-2x)$ 的递增区间，因为 $t(x)$ 是减函数，按照同增递减理论，$\frac{\pi }{3}-2x$ 的增区间应该等于标准正弦函数的减区间，即：$\frac{\pi }{2}+2k\pi \le (\frac{\pi }{3}-2x)\le \frac{3\pi }{2}+2k\pi$

思路5：再求 $f(x)=3\sin (\frac{\pi }{3}-2x)$ 的递减区间，因为 $t(x)$ 是减函数，按照同增递减理论，$\frac{\pi }{3}-2x$ 的减区间应该等于标准正弦函数的增区间，即：$-\frac{\pi }{2}+2k\pi \le (\frac{\pi }{3}-2x)\le \frac{\pi }{2}+2k\pi$