線性代數以矩陣表示,會有諸多特殊名稱,在應用上相當普遍,有必要進行瞭解。有些部份在前面之說明中業已經提到,但在這裡則特別另加說明。
行列式與反矩陣
在工程數學或線性代數中,行列式與反矩陣是常用的矩陣特性。尤其在討論聯立方程式之解的過程中更常用到。反矩陣有如一個矩陣的倒數,一個方矩陣若為A,則其反矩陣可以A
-1表示,而其與原矩陣之關係為:
AA-1=I A-1A=I
其中,I稱為單位矩陣(Identity matrix),其大小為方矩陣,而對角線元素值均為1。在MATLAB中有一個指令稱為eye,可以用以建立這種單位矩陣。例如:
eye(4)
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
矩陣A之反矩陣以inv(A)表示,有如一個數之倒數一樣。例如,設A為一魔術方陣magic(4):
A=rand(4)
A =
0.9355 0.0579 0.1389 0.2722
0.9169 0.3529 0.2028 0.1988
0.4103 0.8132 0.1987 0.0153
0.8936 0.0099 0.6038 0.7468
其反矩陣即為inv(A)表示,其結果設為B,則:
B=inv(A)
B =
-1.5054 3.6825 -1.4860 -0.4013
5.3255 -7.0376 3.9063 -0.1473
-20.0637 22.9531 -8.5486 1.3769
17.9531 -22.8718 8.6384 0.7080
根據定義,原矩陣與其反矩陣相乘應等於單位矩陣,且相乘之順序不拘,亦即:A*B與B*A均應等於I:
B*A
ans =
1.0000 0.0000 0.0000 -0.0000
0.0000 1.0000 -0.0000 0.0000
-0.0000 0.0000 1.0000 -0.0000
-0.0000 0.0000 -0.0000 1.0000
上述結果即為單位矩陣,可以試試以A*B,其結果應相同。此處A、B及I均為方矩陣,且A矩陣之行列式值或det(A)需不得為零,否則其反矩陣不能存在。此種矩陣不存在的情形,稱為奇異矩陣(singular)。一個矩陣若具奇異特性,則其行列值為零,例如:
D=magic(4)
D =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
d=det(D)
d = 0
行值式之值為零,表示其反矩陣不存在,故即使用inv(D)指令也會產生一些數字,但其結果並不可靠,而且會有一些警告訊息出現,例如:
dd=inv(D)
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 1.306145e-017.
dd =
1.0e+014 *
0.9382 2.8147 -2.8147 -0.9382
2.8147 8.4442 -8.4442 -2.8147
-2.8147 -8.4442 8.4442 2.8147
-0.9382 -2.8147 2.8147 0.9382
上述結果之值也變成很大,顯然不是正確的值。不信的話可以用
AA-1=I, A-1A=I 印證一下(在此至少證實一下「垃圾進拉圾出(Gabage in, gabage out」這句名言)。
所以,某矩陣是否為奇異矩陣,可以使用det進行檢驗。其值若為零則屬奇異矩陣。
特徵值及特徵向量(Eigen Value & Eigen Vector)
線性代數中,最重要的工具是利用特徵值與特徵向量(Eigenvalues & Eigenvectors)來說明方矩陣之多項式特性,此兩者均為方型矩陣。利用矩陣之操作,可以作出相等效果之矩陣等式,但型式更為簡化,或容易得解。設特徵矩陣值與特徵向量其分別為D與V,則其與原矩陣A之關係如下:
A * V= V * D
假設有一個方矩陣A係由亂數函數產生,其V與D可以利用eig(A)指令如下求得:
A=rand(3);
[V, D]= eig(A)
A =
0.4103 0.3529 0.1389
0.8936 0.8132 0.2028
0.0579 0.0099 0.1987
V =
0.4053 0.6812 0.0680
0.9136 -0.7124 -0.4004
0.0319 -0.1688 0.9138
D =
1.2167 0 0
0 0.0068 0
0 0 0.1987
A*V
ans =
0.4931 0.0046 0.0135
1.1116 -0.0048 -0.0796
0.0388 -0.0011 0.1816
V*D
ans =
0.4931 0.0046 0.0135
1.1116 -0.0048 -0.0796
0.0388 -0.0011 0.1816
由上述的演算,得知A*V及V*D是一樣的。eig()之指令尚有另外一種型式,即:
[V,D] = eig(A,B)
其中,AB分別為兩矩陣,D為對角矩陣特徵值,而V為對應之特徵向量。其關係如下:
A * V = B * V * D
其使用範圍可以參考線性代數的內容。








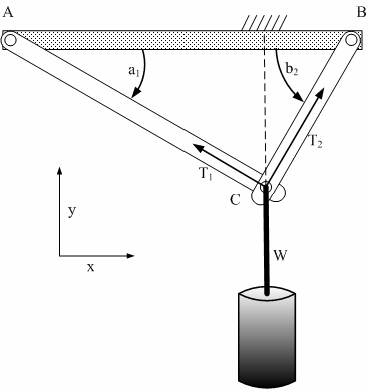
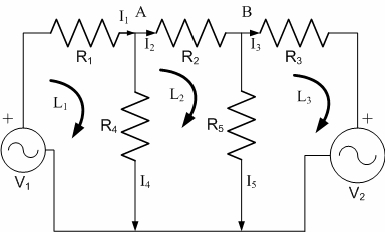
 本文详细介绍了如何使用MATLAB解决线性联立方程组,涵盖了矩阵运算、线性方程组的解法,包括左除法、反矩阵法,并通过多个实际例子,如桁架负重分析、电电路分析和热传导问题,来展示MATLAB在工程问题中的应用。此外,还探讨了稀疏矩阵和相关指令在数值分析中的重要性。
本文详细介绍了如何使用MATLAB解决线性联立方程组,涵盖了矩阵运算、线性方程组的解法,包括左除法、反矩阵法,并通过多个实际例子,如桁架负重分析、电电路分析和热传导问题,来展示MATLAB在工程问题中的应用。此外,还探讨了稀疏矩阵和相关指令在数值分析中的重要性。

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 4651
4651

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








