1、埃拉托斯特尼筛法,简称埃氏筛或爱氏筛,是一种公元前250年由古希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。
给出要筛数值的范围n,找出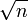 以内的素数
以内的素数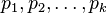 。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个质数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个质数5筛,把5留下,把5的倍数剔除掉;不断重复下去......。
。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个质数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个质数5筛,把5留下,把5的倍数剔除掉;不断重复下去......。
步骤
详细列出算法如下:
- 列出2以后的所有序列:
- 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
- 标出序列中的第一个素数,也就是2,序列变成:
- 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
- 将剩下序列中,划摽2的倍数(用红色标出),序列变成:
- 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
- 如果现在这个序列中最大数小于最后一个标出的素数的平方,那么剩下的序列中所有的数都是素数,否则回到第二步。
- 本例中,因为25大于2的平方,我们返回第二步:
- 剩下的序列中第一个素数是3,将主序列中3的倍数划出(红色),主序列变成:
- 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
- 我们得到的素数有:2,3
- 25仍然大于3的平方,所以我们还要返回第二步:
- 现在序列中第一个素数是5,同样将序列中5的倍数划出,主序列成了:
- 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
- 我们得到的素数有:2 3 5 。
- 因为25等于5的平方,跳出循环.
结论:去掉红色的数字,2到25之间的素数是:2 3 5 7 11 13 17 19 23。
2、试除法
- 尝试从2到
 的整数是否整除N。
的整数是否整除N。
3、AKS质数测试
重要性
AKS最关键的重要性在于它是第一个被发表的一般的,多项式的,确定性的和无限定的质数判定算法。先前的算法至多达到了其中三点,但从未达到全部四个。
- AKS算法可以被用于检测任何一般的给定数字是否为质数。很多已知的高速判定算法仅对满足特定条件的算法适用。例如,用于梅森素数的卢卡斯-莱默检验法仅对梅森素数适用,而Pépin测试仅对费马素数适用。
- 算法的最长运行时间可以被标识为一个关于目标数字长度的多项式。ECPP和APR能够判断一个给定数字是否为质数,但无法对所用输入给出多项式时间范围。
- 算法可以确定性地判断一个给定数字是质数或是合数。随机测试,例如米勒-拉宾检验和Baillie–PSW,可以在多项式时间内对给定数字进行校验,但只能给出概率性的结果。
- AKS算法的正确性是不限定于任何辅助性未证明猜想的。一个反例是米勒-拉宾检验:该算法可以在多项式时间内对所有输入给出确定性结果,但其正确性却基于尚未被证明的广义黎曼猜想。
概念
AKS 质数测试主要是基于以下定理:整数n (≥ 2)是质数,当且仅当
这个同余多项式对所有与n互质的整数a均成立。 这个定理是费马小定理的一般化,并且可以简单的使用二项式定理跟二项式系数的这个特征:
-
 ,对任何
0 < k < n ,当且仅当
n 是质数
,对任何
0 < k < n ,当且仅当
n 是质数
来证明出此定理。
虽然说关系式 (1) 基本上构成了整个质数测试,但是验证花费的时间却是对数时间。因此,为了减少计算复杂度, AKS改确认了以下的同余多项式:
这个多项式与
存在多項式 f 與 g,令:
意义是等同的。
这个同余式可以在多项式时间之内检查完毕。这里我们要注意所有的质数必定满足此条件式 (令 g = 0 则 (3) 等于 (1),因此符合 n 必定是质数)。 然而,有一些合数也会满足这个条件式。有关AKS正确性的证明包含了推导出存在一个够小的r以及一个够小的整数集合A,令如果此同余式对所有A里面的整数都满足,则n必定为质数。
历史以及运算时间
在上文引用的论文的第一版本中,作者们证明了算法的渐近时间为Õ(log 12(n))。换言之,算法使用少于n的数字长度的十二次方乘以一个(数字长度的)多重对数。但是,论文证明的时间上界却过于宽松;事实上,一个被普遍相信的关于索菲热尔曼质数分布的假设如果为真,则会立即将最坏情况减至Õ(log 6(n))。
在这一发现后的几个月中,新的变体陆续出现(Lenstra 2002, Pomerance 2002, Berrizbeitia 2003, Cheng 2003, Bernstein 2003a/b, Lenstra和Pomerance 2003)并依次提高了算法的速度(以改进幅度为序)。由于这些变体的出现,Crandall和Papadopoulos在其科学论文“AKS-类质数测试的实现”(2003年三月发表)中将其称为算法的“AKS-类”。
出于对这些变体和其他回复的回应,论文“质数属于P”稍后被进行了更新,新版本包括了一个AKS算法的正规公式化表述和其正确性证明。(这一版本在Annals of Mathematics上发表。)虽然基本思想没有变化,r却被采用了新方法进行选择,而正确性证明也变得更加紧致有序。与旧证明依赖于许多不同的方法不同,新版本几乎只依赖于有限域上的分圆多项式的特征。新版本同时也优化了时间复杂度的边界到Õ(log 10.5(n))。通过筛法获得的其他结果可以将其进一步简化到Õ(log 7.5(n))。
在2005年,Carl Pomerance和H. W. Lenstra, Jr.展示了一个AKS的变体,可以在Õ(log6(n))次操作内完成测试(n是被测试数)。对于原算法的Õ(log12(n))边界而言,这是一个显著的改进。[2]
算法
整个算法的操作如下:[1]
- 输入:整数 n > 1
- 若存在整数a > 0 且b > 1 ,令 n = ab ;则输出合数
- 找出最小的 r 令 or(n) > log2(n).
- 若 对某些a ≤ r,1 < gcd(a,n) < n,输出合数。
- 若 n ≤ r, 输出质数。
- 对 a = 1 到
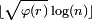 的所有数,
的所有数,
- 如果 ( X+ a) n≠ X n+ a (mod X r − 1, n), 输出 合数。
- 输出 质数。
这里的 or(n)是n mod r的目。 另外,这里的log 代表以二为底的对数,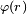 则是r的欧拉函数。
则是r的欧拉函数。
下面说明若n是个质数,那么算法总是会返回质数:由于n是质数,步骤1和3永远不会返回合数。步骤5也不会返回合数,因为(2)对所有质数n为真。因此,算法一定会在步骤4或6返回质数。
对应地,如果n是合数,那么算法一定返回合数:如果算法返回质数,那么则一定是从步骤4或6返回。对于前者,因为n ≤ r, n必然有因子a ≤ r符合1 < gcd(a,n) < n,因此会返回合数。剩余的可能性就是步骤6,在文章[1]中,这种情况被证明不会发生,因为在步骤5中检验的多个等式可以确保输出一定是合数。







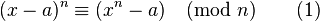


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








