规定该有心斥力场中斥力满足的形式为

其中,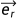 为矢径的方向向量。
为矢径的方向向量。
以有心力场中心为原点建立极坐标,质点在斥力场中运动极坐标方程如下所示

其中, 参数和
参数和 参数的含义分别
参数的含义分别


其中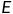 为质点在有心斥力场中势能和动能之和,
为质点在有心斥力场中势能和动能之和,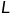 为质点对有心力场中心的角动量。具体的可以看下图中的解释。
为质点对有心力场中心的角动量。具体的可以看下图中的解释。
下面为推导过程

注意,为了使双曲线右焦点与有心斥力场中心重合,且双曲线左支恰好为质点运动的轨迹。我强行把不定积分得到的常数c确定为π。这个做法是可行的,就是考虑实际物理情况,舍去非物理解。
规定该有心斥力场中斥力满足的形式为

其中,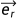 为矢径的方向向量。
为矢径的方向向量。
以有心力场中心为原点建立极坐标,质点在斥力场中运动极坐标方程如下所示

其中, 参数和
参数和 参数的含义分别
参数的含义分别


其中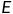 为质点在有心斥力场中势能和动能之和,
为质点在有心斥力场中势能和动能之和,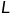 为质点对有心力场中心的角动量。具体的可以看下图中的解释。
为质点对有心力场中心的角动量。具体的可以看下图中的解释。
下面为推导过程

注意,为了使双曲线右焦点与有心斥力场中心重合,且双曲线左支恰好为质点运动的轨迹。我强行把不定积分得到的常数c确定为π。这个做法是可行的,就是考虑实际物理情况,舍去非物理解。
 103
103

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


