物理法求阿基米德螺旋线曲率半径

一、问题描述

已知阿基米德螺旋线在极坐标平面可以表示为，其中为常实数。求任意角度处的曲率半径。

阿基米德螺旋线

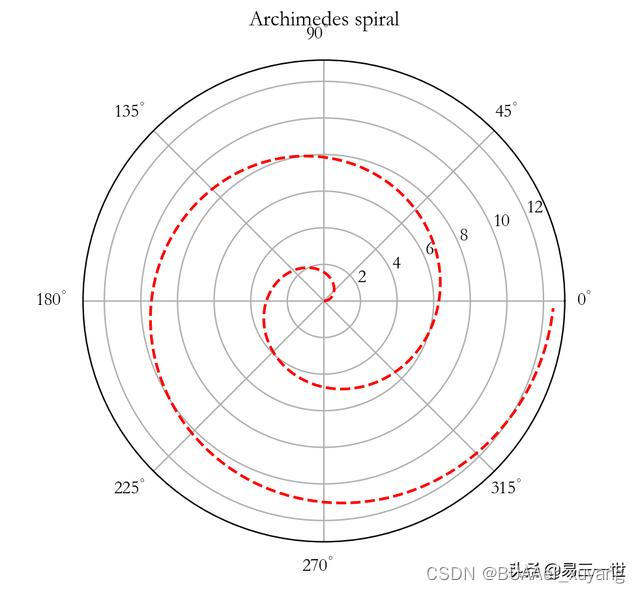
二、曲率半径的求解思路

当一质点沿着任意曲线运动并运动到曲线上A点时，其在A点的加速度可分解为切向和方向。法向加速度满足

其中v为质点沿着曲线运动的速率，即为曲率半径。

构造一个运动，使质点以恒定且已知的速率沿着阿基米德螺旋线运动，设法求出其在任意角度的加速度，便能导出在任意任意角度的曲率半径。

这个运动是具有现实意义的，是符合事实的。试想，若存在一个阿基米德形的管道，从管道的一端以某一速率射入一个小球。那么，小球将以恒定的速率在管道中运动。

三、加速度的求解思路

思路和圆周运动一样。由于速度为矢量，将时刻和时刻的速度矢量的起点平移到一起，并作差，将得到了速度的改变量。与的商（矢量）即为加速度矢量。

在我们预设的阿基米德螺旋线运动中，由于速率不变，也即速度矢量的模长不变，考察速度矢量方向改变的快慢即可。

四、绘制出小量三角形进行分析

某时刻，小球（质点）运动到A点，角位置为 。经过的时间，小球运动的B点，角位置改变量为 ，如下图所示。

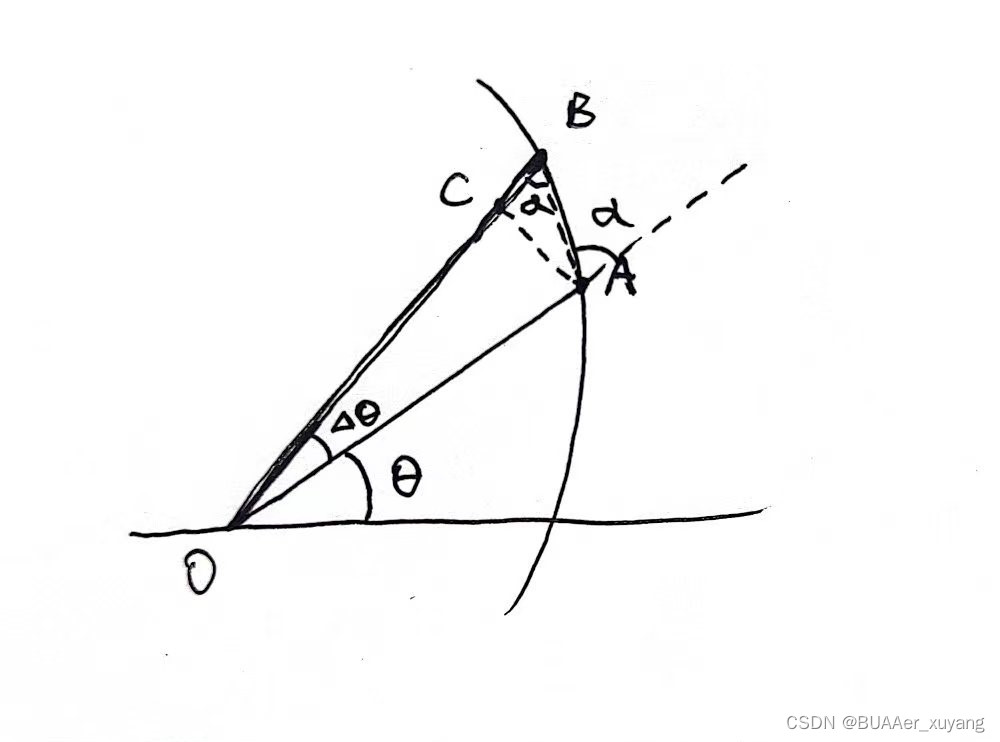
 由此，我们能推出一下结论：

1. 
2. 
3. 
4. 

注意到 ，将其设为 。那么有：

 

由于A和B非常接近，可以认为AB的方向即为A点速度的方向（参考速度的定义）。那么，速度的角度可以表示为

同样，速度的模可以表示为AB的长度和时间微分的商，也即

其中，可以表示为

这样可以得出

如果小球速率不变，那么其加速度的模等于其速度的模和角度变化率的乘积，如下图所示。

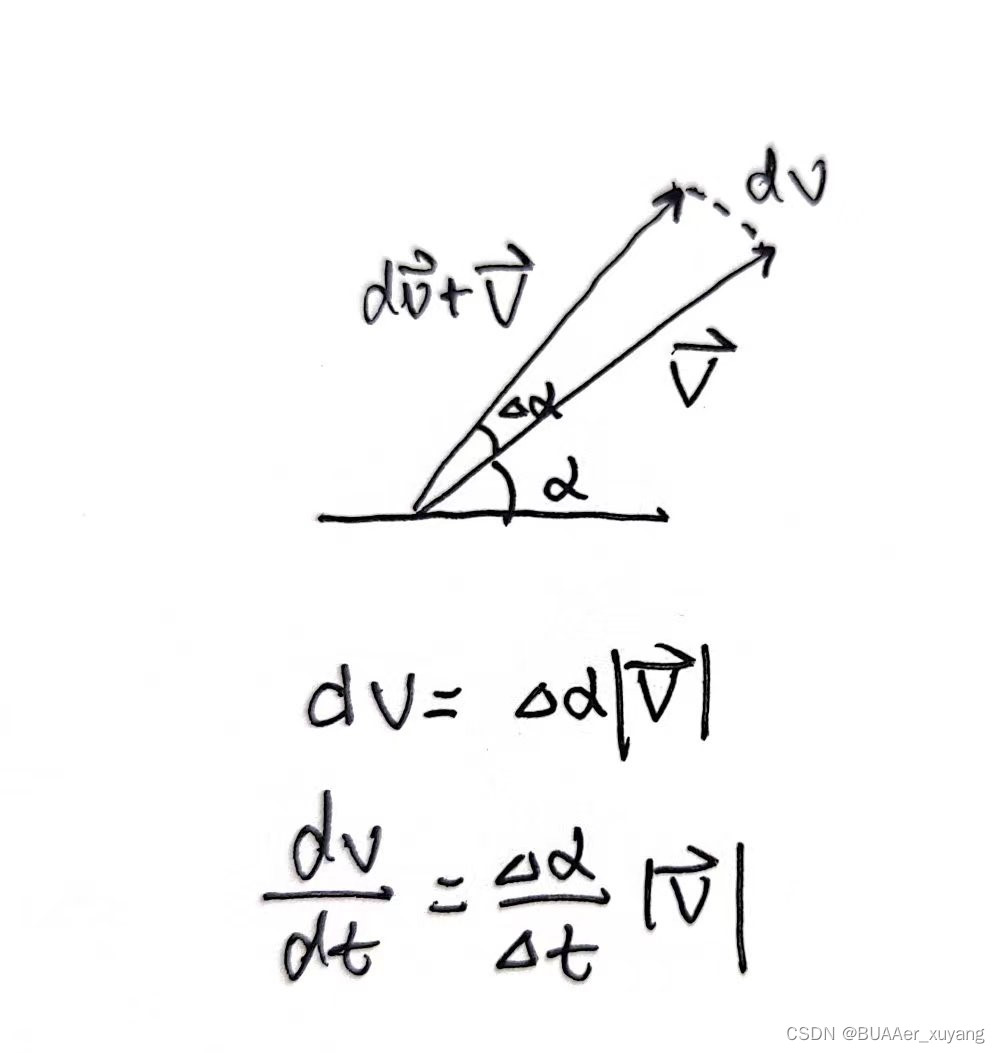
注意，小球速度矢量和极轴的夹角为，对其关于时间求导

于是，加速度可以求

所以，曲率半径可以表示为