51Nod - 1009 数位dp

题意：

     题目链接： https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1009

给定一个十进制正整数N，写下从1开始，到N的所有正数，计算出其中出现所有1的个数。

例如：n = 12，包含了5个1。1,10,12共包含3个1，11包含2个1，总共5个1。

Input

输入N(1 <= N <= 10^9)

Output

输出包含1的个数

Input示例

12

Output示例

5

思路：

一道基础的数位dp，当作入门题也挺好

套用网上大多的数位dp模板，这里dp[pos]表示在没有上界的限制条件下，从pos位到最低位能组成的数一共有多少个1，简单来说，其实就是0到((10^pos) -1)有多少个1。

数位dp其实就是一位一位的向下递归下去，每次枚举一位上的每一个数， 这样就可以构成一棵树，比如就21这个上界举例，dfs构成的搜索数如下图所示：

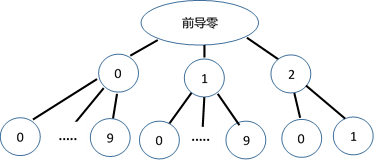
dfs中的pos表示当前搜索到达第几位，num表示经过搜索树层层递归下来的路径上有几个节点数字是1，limit就是模板中的标明是否是上界的标志。

关于记忆化搜索的部分，当没有limit限制的时候，就可以返回当前的保存的值，这里返回的num * ten[pos + 1] + dp[pos]值得仔细思考，其中ten[pos]表示10^pos，前一部分num*ten[pos]表示的是路径上的数字为1的节点在子树中会出现10^pos次，举例来说，假设现在已经枚举到百位之前枚举的数字是131，那么接下来的需要计算的所有数字都是131xx，(也就是从是13100~13199）100个数字，那么也就是说前面路径131中的两个1一共出现了100次，所以要乘起来；后一部分dp[pos]很好理解，就是计算在13100到13199之间的数131xx在xx部分会出现的1的数目；这样这两部分加起来就是这条路搜索的答案。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll dp[20], a[20],ten[20];

void init() {
    ten[0] = 1;
    for (int i = 1; i <= 10; i++)
        ten[i] = ten[i - 1] * 10;
}

ll dfs(int pos, int num, int limit) {
    if (pos == -1) return num;
    if (!limit && dp[pos] != -1) return num * ten[pos + 1] + dp[pos];
    int up = limit ? a[pos] : 9;
    ll res = 0;
    for (int i = 0; i <= up; i++) {
        if (i == 1) res += dfs(pos - 1, num + 1, limit && i == a[pos]);
        else res += dfs(pos - 1, num, limit && i == a[pos]);
    }
    if (!limit) dp[pos] = res;
    return res;
}

ll solve(ll x) {
    int pos = 0;
    while (x) {
        a[pos++] = x % 10;
        x /= 10;
    }
    return dfs(pos - 1, 0, true);
}

int main(){
    init();
    int n;
    scanf("%d", &n);
    memset(dp, -1, sizeof(dp));
    cout << solve(n) << endl;
    return 0;
}