理解卷积、单通道卷积、深度卷积(多通道卷积)、逐点卷积、实战YoloV1卷积网络 、池化计算

---

---

卷积计算

单通道卷积

最基础的卷积过程，必须理解这个过程

计算过程

1. 确定图像大小
2. 确定Stride步长
3. 确定Padding扩充

设图像大小为（5，5，1），长为5，宽为5，1个通道

设卷积核大小为（3，3），stride=1，padding=0

综上所述我们得到W=5，F=3，P=0，S=1

计算公式

outputSize = [( W-F+2*P ) / S] + 1

计算结果

= (5-3+0)/1+1=3最终size为3*3，卷积核数量为1所以为（3，3，1）

多通道卷积（深度卷积）

计算过程

1. 确定图像大小（彩色图像比二维多一个通道channel数）
2. 确定Stride步长
3. 确定Padding扩充

设图像大小为（5，5，3），长为5，宽为5，3个通道（RGB）

设卷积核大小为（3，3，3），stride=1，padding=0

卷积核的数量为1，卷积核的通道数为3

综上所述我们得到W=5，F=3，P=0，S=1

计算结果

因为只有一个卷积核所以最后得到的channel是1。

Input(5,5,3)----Conv(3,3,3)---->Output(3,3,1)

遵循公式

输入的通道数 === 卷积核的通道数

输出的通道数 === 卷积核的个数

假设输入层为一个大小为64×64像素、三通道彩色图片。经过一个包含4个Filter的卷积层，最终输出4个Feature Map，且尺寸与输入层相同。整个过程可以用下图来概括。

逐通道卷积

同样是上述例子，一个大小为64×64像素、三通道彩色图片首先经过第一次卷积运算，不同之处在于此次的卷积完全是在二维平面内进行，且Filter的数量与上一层的Depth相同。所以一个三通道的图像经过运算后生成了3个Feature map，如下图所示：

逐点卷积

逐点卷积就是多通道卷积的特殊形式，每个卷积核为（1，1）大小。
Pointwise Convolution的运算与常规卷积运算非常相似，不同之处在于卷积核的尺寸为 1×1×M，M为上一层的depth。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合，生成新的Feature map。有几个Filter就有几个Feature map。如下图所示：

计算过程

使用（1，1，numOfChannels ) 的卷积核进行卷积

思想：使用1x1卷积核，实现降维和升维的操作其实就是channel间信息的线性组合变化，3x3，64channels的卷积核后面添加一个1x1，28channels的卷积核，就变成了3x3，28channels的卷积核，原来的64个channels就可以理解为跨通道线性组合变成了28channels，这就是通道间的信息交互。

可以实现

可以实现在（width，height）不变的情况下，修改channel的数量。

Separable Convolution深度可分离卷积

回顾一下，常规卷积的参数个数为：

N_std = 4 × 3 × 3 × 3 = 108

Separable Convolution（Depthwise Convolution + Pointwise Convolution）的参数由两部分相加得到：

N_depthwise = 3 × 3 × 3 = 27
N_pointwise = 1 × 1 × 3 × 4 = 12
N_separable = N_depthwise + N_pointwise = 39

相同的输入，同样是得到4张Feature map，Separable Convolution的参数个数是常规卷积的约1/3。因此，在参数量相同的前提下，采用Separable Convolution的神经网络层数可以做的更深。

池化计算

Max-Pooling：选择这个框里最大的一个进行输出

如（2，2）的框里，会让图像（width，height）变为（width/2，height/2）

计算公式

Output=(W- F)/S+1

计算实战-YoloV1网络结构

网络结构：Conv+Fully Connected

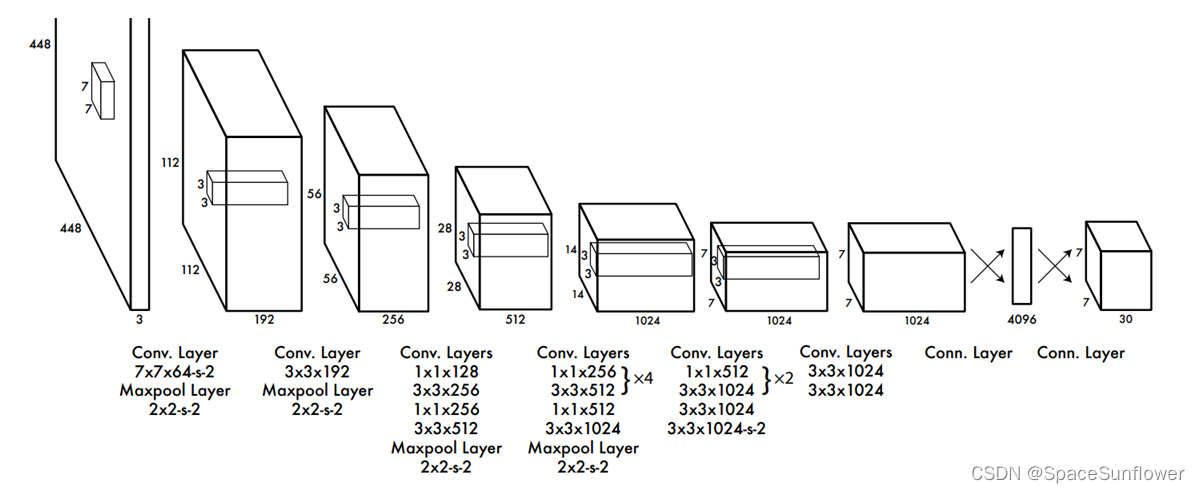
Layer	Stride,Padding	Output
input		（448，448，3）
Conv (7,7,64)	S=2,P=3	（224，224，64）
Maxpooling	S=2	（112，112，64）
Conv (3,3,192)	S=1,P=1	（112，112，192）
Maxpooling	S=2	（56，56，192）
Conv (1,1,128)	S=1,P=1	（56，56，128）
Conv (3,3,256)	S=1,P=1	（56，56，256）
Conv (1,1,256)	S=1	（56，56，256）
Conv (3,3,512)	S=1,P=1	（56，56，512）
Maxpooling	S=2	（28，28，512）
Conv (1,1,256)	S=1	（28，28，256）
Conv (3,3,512)	S=1,P=1	（28，28，512）
Conv (1,1,256)	S=1	（28，28，256）
Conv (3,3,512)	S=1,P=1	（28，28，512）
Conv (1,1,256)	S=1	（28，28，256）
Conv (3,3,512)	S=1,P=1	（28，28，512）
Conv (1,1,256)	S=1	（28，28，256）
Conv (3,3,512)	S=1,P=1	（28，28，512）
Conv (1,1,512)	S=1	（28，28，512）
Conv (3,3,1024)	S=1,P=1	（28，28，1024）
Maxpooling	S=2	（14，14，1024）
Conv (1,1,512)	S=1	（14，14，512）
Conv (3,3,1024)	S=1,P=1	（14，14，1024）
Conv (1,1,512)	S=1	（14，14，512）
Conv (3,3,1024)	S=1,P=1	（14，14，1024）
Conv (3,3,1024)	S=1,P=1	（14，14，1024）
Conv (3,3,1024)	S=2,P=1	（7，7，1024）
Conv (3,3,1024)	S=1,P=1	（7，7，1024）
Conv (3,3,1024)	S=1,P=1	（7，7，1024）

附带理解过程的：

为什么在这里写理解过程，是希望大家纠正我的理解过程，按照我的理解方法，每一层之间卷积核所需要的参数量非常大。我的理解哪里有问题？

Layer	Stride,Padding	Output	理解过程
input		（448，448，3）
Conv (7,7,64)	S=2,P=3	（224，224，64）	多通道卷积，每个filter3层，共64个filter
Maxpooling	S=2	（112，112，64）	Maxpooling
Conv (3,3,192)	S=1,P=1	（112，112，192）	多通道卷积，每个filter64层，共192个filter
Maxpooling	S=2	（56，56，192）	Maxpooling
Conv (1,1,128)	S=1,P=1	（56，56，128）	逐点卷积，每个filter(1,1)有192个，共128个filter
Conv (3,3,256)	S=1,P=1	（56，56，256）	多通道卷积，每个filter128层，共256个filter
Conv (1,1,256)	S=1	（56，56，256）	逐点卷积，每个filter(1,1)有256个，共256个filter
Conv (3,3,512)	S=1,P=1	（56，56，512）	多通道卷积，每个filter256层，共512个filter
Maxpooling	S=2	（28，28，512）	Maxpooling
Conv (1,1,256)	S=1	（28，28，256）	逐点卷积，每个filter(1,1)有512个，共256个filter
Conv (3,3,512)	S=1,P=1	（28，28，512）	多通道卷积，每个filter256层，共512个filter
Conv (1,1,256)	S=1	（28，28，256）	逐点卷积，每个filter(1,1)有512个，共256个filter
Conv (3,3,512)	S=1,P=1	（28，28，512）	多通道卷积，每个filter256层，共512个filter
Conv (1,1,256)	S=1	（28，28，256）	逐点卷积，每个filter(1,1)有512个，共256个filter
Conv (3,3,512)	S=1,P=1	（28，28，512）	多通道卷积，每个filter256层，共512个filter
Conv (1,1,256)	S=1	（28，28，256）	逐点卷积，每个filter(1,1)有512个，共256个filter
Conv (3,3,512)	S=1,P=1	（28，28，512）	多通道卷积，每个filter256层，共512个filter
Conv (1,1,512)	S=1	（28，28，512）	逐点卷积，每个filter(1,1)有512个，共512个filter
Conv (3,3,1024)	S=1,P=1	（28，28，1024）	多通道卷积，每个filter512层，共1024个filter
Maxpooling	S=2	（14，14，1024）	Maxpooling
Conv (1,1,512)	S=1	（14，14，512）	逐点卷积，每个filter(1,1)有1024个，共512个filter
Conv (3,3,1024)	S=1,P=1	（14，14，1024）	多通道卷积，每个filter512层，共个1024filter
Conv (1,1,512)	S=1	（14，14，512）	逐点卷积，每个filter(1,1)有1024个，共512个filter
Conv (3,3,1024)	S=1,P=1	（14，14，1024）	多通道卷积，每个filter512层，共1024个filter，修改channel
Conv (3,3,1024)	S=1,P=1	（14，14，1024）	多通道卷积，每个filter1024层，共1024个filter，提取边缘特征
Conv (3,3,1024)	S=2,P=1	（7，7，1024）	多通道卷积，每个filter1024层，共1024个filter，提取边缘特征
Conv (3,3,1024)	S=1,P=1	（7，7，1024）	多通道卷积，每个filter1024层，共1024个filter，提取边缘特征
Conv (3,3,1024)	S=1,P=1	（7，7，1024）	多通道卷积，每个filter1024层，共1024个filter，提取边缘特征

这里用到的卷积核有三种

（3，3，1） Stride=1,Padding=1

可以实现，width和height不变的情况下，改变channels的数量

可以实现提取原来的特征，保持width和height不变的情况下，改变channels的数量

（3，3） Stride=2,Padding=1

实现（width/2，height/2）
通常channels数量与输入图像的channels相同
如果采用（6，6）输入图像，（3，3）卷积，stride=2，padding=1，会导致边缘信息没法获取到。

所以我们应该采用（3，3） Stride=2,Padding=1的卷积

这样的情况下就可以提取到原来图像中的边缘信息，最后得到的图像大小变为原来图像大小的1/4

（1，1，num of channels） Stride=1,Padding=0

逐点卷积修改channels数量

参考链接

[【基础积累】1x1卷积到底有哪些用处？ - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/145566635#:~:text=1x1卷积核： 如果卷积的输出输入都只是一个平面，那么1x1卷积核并没有什么意义，它是完全不考虑像素与周边其他像素关系。 但卷积的输出输入是长方体，所以 1x1卷积实际上是对每个像素点，在不同的channels上进行线性组合（信息整合），且保留了图片的原有平面结构，调控depth，从而完成升维或降维的功能。,1x1卷积核的作用 1x1卷积的作用可以总结为以下三点： 可以实现信息的跨通道整合和交互 具有降维和升维的能力，减少网络参数。 这里的维度指的是卷积核通道数（厚度），而不改变图片的宽和高。)

深度学习 | CNN卷积核与通道-CSDN博客

https://blog.csdn.net/zhw864680355/article/details/105453945