大数据、人工智能、海难搜救、生物医学、邮件过滤,这些看起来彼此不相关的领域之间有什么联系?答案是,它们都会用到同一个数学公式——贝叶斯公式。它虽然看起来很简单、很不起眼,但却有着深刻的内涵。那么贝叶斯公式是如何从默默无闻到现在广泛应用、无所不能的呢?
一 什么是贝叶斯公式
18世纪英国业余数学家托马斯·贝叶斯(Thomas Bayes,1702~1761)提出过一种看上去似乎显而易见的观点:“用客观的新信息更新我们最初关于某个事物的信念后,我们就会得到一个新的、改进了的信念。” 这个研究成果,因为简单而显得平淡无奇,直到他死后的两年才于1763年由他的朋友理查德·普莱斯帮助发表。它的数学原理很容易理解,简单说就是,如果你看到一个人总是做一些好事,则会推断那个人多半会是一个好人。这就是说,当你不能准确知悉一个事物的本质时,你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。用数学语言表达就是:支持某项属性的事件发生得愈多,则该属性成立的可能性就愈大。与其他统计学方法不同,贝叶斯方法建立在主观判断的基础上,你可以先估计一个值,然后根据客观事实不断修正。
1774年,法国数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace,1749-1827)独立地再次发现了贝叶斯公式。拉普拉斯关心的问题是:当存在着大量数据,但数据又可能有各种各样的错误和遗漏的时候,我们如何才能从中找到真实的规律。拉普拉斯研究了男孩和女孩的生育比例。有人观察到,似乎男孩的出生数量比女孩更高。这一假说到底成立不成立呢?拉普拉斯不断地搜集新增的出生记录,并用之推断原有的概率是否准确。每一个新的记录都减少了不确定性的范围。拉普拉斯给出了我们现在所用的贝叶斯公式的表达:
P(A/B)=P(B/A)*P(A)/P(B),
该公式表示在B事件发生的条件下A事件发生的条件概率,等于A事件发生条件下B事件发生的条件概率乘以A事件的概率,再除以B事件发生的概率。公式中,P(A)也叫做先验概率,P(A/B)叫做后验概率。严格地讲,贝叶斯公式至少应被称为“贝叶斯-拉普拉斯公式”。
二 默默无闻200年
贝叶斯公式现在已经非常流行,甚至在热门美剧《生活大爆炸》中谢耳朵也秀了一下。但它真正得到重视和广泛应用却是最近二三十年的事,其间被埋没了200多年。这是为什么呢?原因在于我们有另外一种数学工具——经典统计学,或者叫频率主义统计学(我们在学校学的主要是这种统计学),它在200多年的时间里一直表现不错。从理论上讲,它可以揭示一切现象产生的原因,既不需要构建模型,也不需要默认条件,只要进行足够多次的测量,隐藏在数据背后的原因就会自动揭开面纱。
在经典统计学看来,科学是关于客观事实的研究,我们只要反复观察一个可重复的现象,直到积累了足够多的数据,就能从中推断出有意义的规律。而贝叶斯方法却要求科学家像算命先生一样,从主观猜测出发,这显然不符合科学精神。就连拉普拉斯后来也放弃了贝叶斯方法这一思路,转向经典统计学。因为他发现,如果数据量足够大,人们完全可以通过直接研究这些样本来推断总体的规律。
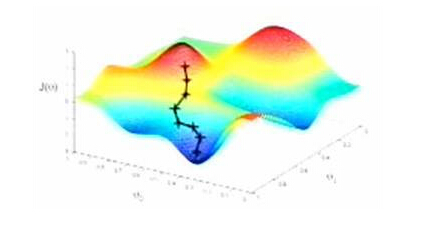
打个比方来帮助我们理解这两种统计学方法的区别。假如我们想知道某个区域里海拔最低的地方,经典统计学的方法是首先进行观测,取得区域内不同地方的海拔数据,然后从中找出最低点。这个数据量必须足够多,以反映区域内地形全貌的特征,这样我们才能相信找到的就是实际上的最低点。而贝叶斯方法是我不管哪里最低,就凭感觉在区域内随便选个地方开始走,每一步都往下走,虽然中间可能有一些曲折,但相信这样走早晚能够到达最低点。可以看出,贝叶斯方法的关键问题是这个最终到达的低点可能不是真正的最低点,而是某个相对低点,它可能对该区域的地形(碗型、马鞍形等)和最初我们主观选择的出发点有依赖性。如果问题域是碗型的,我们到达的就是最低点;但如果是马鞍形或者其他复杂曲面,那么我们到达的可能是多个相对低点(极点)中的一个,而不是真正的最低点。这是贝叶斯方法最受经典统计学方法诟病的原因,也是它在过去的200多年被雪藏的原因所在。
贝叶斯方法原理示意图:
三 初显威力
长期以来,贝叶斯方法虽然没有得到主流学界的认可,但其实我们经常会不自觉地应用它来进行决策,而且还非常有效。比如炮兵在射击时会使用贝叶斯方法进行瞄准。炮弹与子弹不同,它的飞行轨迹是抛物线,瞄准的难度更大,因此他们会先根据计算和经验把炮管调整到一个可能命中的瞄准角度(先验概率),然后再根据炮弹的实际落点进行调整(后验概率),这样在经过2-3次射击和调整后炮弹就能够命中目标了。
在日常生活中,我们也常使用贝叶斯方法进行决策。比如在一个陌生的地方找餐馆吃饭,因为之前不了解哪家餐馆好,似乎只能随机选择,但实际上并非如此,我们会根据贝叶斯方法,利用以往积累的经验来提供判断的线索。经验告诉我们,通常那些坐满了客人的餐馆的食物要更美味些,而那些客人寥寥的餐馆,食物可能不怎么样而且可能会被宰。这样,我们就往往通过观察餐厅的上座率来选择餐馆就餐。这就是我们根据先验知识进行的主观判断。在吃过以后我们对这个餐馆有了更多实际的了解,以后再选择时就更加容易了。所以说,在我们认识事物不全面的情况下,贝叶斯方法是一种很好的利用经验帮助作出更合理判断的方法。
而两个标志性的事件在让学术界开始重视贝叶斯方法上起到了重要作用。
1.联邦党人文集作者公案
1787年5月,美国各州(当时为13个)代表在费城召开制宪会议;1787年9月,美国的宪法草案被分发到各州进行讨论。一批反对派以“反联邦主义者”为笔名,发表了大量文章对该草案提出批评。宪法起草人之一亚历山大·汉密尔顿着急了,他找到曾任外交国务秘书(即后来的国务卿)的约翰·杰伊,以及纽约市国会议员麦迪逊,一同以普布利乌斯(Publius)的笔名发表文章,向公众解释为什么美国需要一部宪法。他们走笔如飞,通常在一周之内就会发表3-4篇新的评论。1788年,他们所写的85篇文章结集出版,这就是美国历史上著名的《联邦党人文集》。
《联邦党人文集》出版的时候,汉密尔顿坚持匿名发表,于是,这些文章到底出自谁人之手,成了一桩公案。1810年,汉密尔顿接受了一个政敌的决斗挑战,但出于基督徒的宗教信仰,他决意不向对方开枪。在决斗之前数日,汉密尔顿自知时日不多,他列出了一份《联邦党人文集》的作者名单。1818年,麦迪逊又提出了另一份作者名单。这两份名单并不一致。在85篇文章中,有73篇文章的作者身份较为明确,其余12篇存在争议。
1955年,哈佛大学统计学教授Fredrick Mosteller找到芝加哥大学的年轻统计学家David Wallance,建议他跟自己一起做一个小课题,他想用统计学的方法,鉴定出《联邦党人文集》的作者身份。
但这根本就不是一个小课题。汉密尔顿和麦迪逊都是文章高手,他们的文风非常接近。从已经确定作者身份的那部分文本来看,汉密尔顿写了9.4万字,麦迪逊写了11.4万字。汉密尔顿每个句子的平均长度是34.55字,而麦迪逊是34.59字。就写作风格而论,汉密尔顿和麦迪逊简直就是一对双胞胎。汉密尔顿和麦迪逊写这些文章,用了大约一年的时间,而Mosteller和Wallance甄别出作者的身份花了10多年的时间。
如何分辨两人写作风格的细微差别,并据此判断每篇文章的作者就是问题的关键。他们所采用的方法就是以贝叶斯公式为核心的包含两个类别的分类算法。先挑选一些能够反映作者写作风格的词汇,在已经确定了作者的文本中,对这些特征词汇的出现频率进行统计,然后再统计这些词汇在那些不确定作者的文本中的出现频率,从而根据词频的差别推断其作者归属。这其实和我们现在使用的垃圾邮件过滤器的原理是一样的。
他们是在没有计算机帮助的条件下用手工处理“大数据”,这一工程的耗时耗力是可想而知的。将近100个哈佛大学的学生帮助他们处理数据。学生们用最原始的方式,用打字机把《联邦党人文集》的文本打出来,然后把每个单词剪下来,按照字母表的顺序,把这些单词分门别类地汇集在一起。有个学生干得累了,伸了个懒腰,长长地呼了一口气。他这一口气用力太猛,一下子把刚刚归置好的单词条吹得如柳絮纷飞,一屋子学生瞬间石化,估计很多人连灭了他的心都有。而这只是手工大数据时代的日常。
Mosteller和Wallance这是要在干草垛里找绣花针。他们首先剔除掉用不上的词汇。比如,《联邦党人文集》里经常谈到“战争”、“立法权”、“行政权”等,这些词汇是因主题而出现,并不反映不同作者的写作风格。只有像“in”,“an”,“of”,“upon”这些介词、连词等才能显示出作者风格的微妙差异。一位历史学家好心地告诉他们,有一篇1916年的论文提到,汉密尔顿总是用“while”,而麦迪逊则总是用“whilst”。但仅仅有这一个线索是不够的。“while”和“whilst”在这12篇作者身份待定的文章里出现的次数不够多。况且,汉密尔顿和麦迪逊有时候会合写一篇文章,也保不齐他们会互相改文章,要是汉密尔顿把麦迪逊的“whilst”都改成了“while”呢?
当学生们把每个单词的小纸条归类、粘好之后,他们发现,汉密尔顿的文章里平均每一页纸会出现两次“upon”,而麦迪逊几乎一次也不用。汉密尔顿更喜欢用“enough”,麦迪逊则很少用。其它一些有用的词汇包括:“there”、“on”等等。1964年,Mosteller和Wallance发表了他们的研究成果。他们的结论是,这12篇文章的作者很可能都是麦迪逊。他们最拿不准的是第55篇,麦迪逊是作者的概率是240:1。
这个研究引起了极大的轰动,但最受震撼的不是宪法研究者,而是统计学家。Mosteller和Wallance的研究,把贝叶斯公式这个被统计学界禁锢了200年的幽灵从瓶子中释放了出来。
2.天蝎号核潜艇搜救
2014年初马航MH370航班失联,所有人都密切关注搜救的进展情况。那么我们是用什么方法在茫茫大海中寻找失联的飞机或者船只的呢?这要从天蝎号核潜艇说起。
1968年5月,美国海军的天蝎号核潜艇在大西洋亚速海海域突然失踪,潜艇和艇上的99名海军官兵全部杳无音信。按照事后调查报告的说法,罪魁祸首是这艘潜艇上的一枚奇怪的鱼雷,发射出去后竟然敌我不分,扭头射向自己,让潜艇中弹爆炸。
为了寻找天蝎号的位置,美国政府从国内调集了包括多位专家的搜索部队前往现场,其中包括一位名叫John Craven的数学家,他的头衔是“美国海军特别计划部首席科学家”。在搜寻潜艇的问题上,Craven提出的方案使用了上面提到的贝叶斯公式。他召集了数学家、潜艇专家、海事搜救等各个领域的专家。每个专家都有自己擅长的领域,但并非通才,没有专家能准确估计到在出事前后潜艇到底发生了什么。有趣的是,Craven并不是按照惯常的思路要求团队成员互相协商寻求一个共识,而是让各位专家编写了各种可能的“剧本”,让他们按照自己的知识和经验对于情况会向哪一个方向发展进行猜测,并评估每种情境出现的可能性。据说,为了给枯燥的工作增加一些趣味,Craven还准备了威士忌酒作为“投注”正确的奖品。
因为在Craven的方案中,结果很多是这些专家以猜测、投票甚至可以说赌博的形式得到的,不可能保证所有结果的准确性,他的这一做法受到了很多同行的质疑。可是因为搜索潜艇的任务紧迫,没有时间进行精确的实验、建立完整可靠的理论,Craven的办法不失为一个可行的办法。
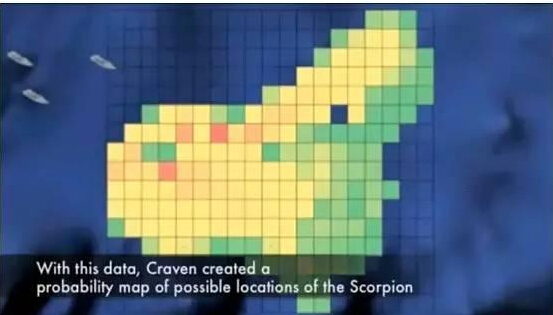
由于失事时潜艇航行的速度快慢、行驶方向、爆炸冲击力的大小、爆炸时潜艇方向舵的指向都是未知量,即使知道潜艇在哪里爆炸,也很难确定潜艇残骸最后被海水冲到哪里。Craven粗略估计了一下,半径20英里的圆圈内的数千英尺深的海底,都是天蝎号核潜艇可能沉睡的地方,要在这么大的范围,这么深的海底找到潜艇几乎成了不可能完成的任务。
贝叶斯Craven把各位专家的意见综合到一起,得到了一张20英里海域的概率图。整个海域被划分成了很多个小格子,每个小格子有两个概率值p和q,p是潜艇躺在这个格子里的概率,q是如果潜艇在这个格子里,它被搜索到的概率。按照经验,第二个概率值主要跟海域的水深有关,在深海区域搜索失事潜艇的“漏网”可能性会更大。如果一个格子被搜索后,没有发现潜艇的踪迹,那么按照贝叶斯公式,这个格子潜艇存在的概率就会降低:
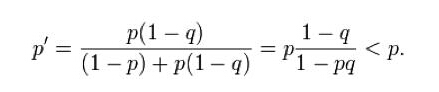
格子潜艇存在的概率由于所有格子概率的总和是1,这时其他格子潜艇存在的概率值就会上升:
格子潜艇存在的概率每次寻找时,先挑选整个区域内潜艇存在概率值最高的一个格子进行搜索,如果没有发现,概率分布图会被“洗牌”一次,搜寻船只就会驶向新的“最可疑格子”进行搜索,这样一直下去,直到找到天蝎号为止。
最初开始搜救时,海军人员对Craven和其团队的建议嗤之以鼻,他们凭经验估计潜艇是在爆炸点的东侧海底。但几个月的搜索一无所获,他们才不得不听从了Craven的建议,按照概率图在爆炸点的西侧寻找。经过几次搜索,潜艇果然在爆炸点西南方的海底被找到了。
由于这种基于贝叶斯公式的方法在后来多次搜救实践中被成功应用,现在已经成为海难空难搜救的通行做法。
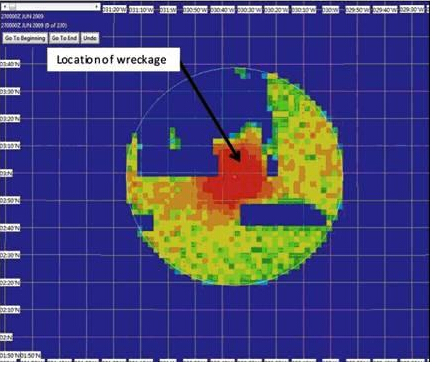
2009年法航空难搜救的后验概率分布图:
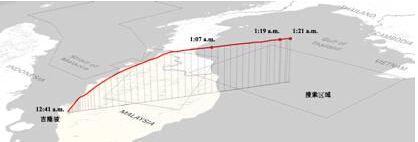
2009年法航空难搜救的后验概率分布图2014马航MH370失联搜索区域:
2014马航MH370失联搜索区域与计算机的结合使贝叶斯公式巨大的实用价值进一步体现出来,它不但为我们提供了一条全新的问题解决路径,带来工具和理念的革命,而且甚至可能是人类大脑本身的认知和构建方式。
贝叶斯公式在联邦党人文集作者公案和天蝎号核潜艇搜救中大显身手后(详见大数据背后的神秘公式(上):贝叶斯公式),开始引起学术界的注意和重视,而其上世纪八十年代在自然语言处理领域的成功,向我们展示了一条全新的问题解决路径。计算能力的不断提高和大数据的出现使它的威力日益显现,一场轰轰烈烈的“贝叶斯革命”正在发生。
一 真正的突破
自然语言处理就是让计算机代替人来翻译语言、识别语音、认识文字和进行海量文献的自动检索。但是人类的语言可以说是信息里最复杂最动态的一部分。人们最初想到的方法是语言学方法,让计算机学习人类的语法、分析语句等等。尤其是在乔姆斯基(有史以来最伟大的语言学家)提出 “形式语言” 以后,人们更坚定了利用语法规则的办法进行文字处理的信念。遗憾的是,几十年过去了,在计算机语言处理领域,基于这个语法规则的方法几乎毫无突破。
其实早在几十年前,数学家兼信息论的祖师爷香农 (Claude Shannon)就提出了用数学方法处理自然语言的想法。遗憾的是当时的计算机根本无法满足大量信息处理的需要,所以他的这一想法并没有引起重视。
率先成功利用数学方法解决自然语言处理问题的是语音和语言处理大师贾里尼克 (Fred J他引入一个全新的视角,认为语音识别就是根据接收到的一个信号序列推测说话人实际发出的信号序列(说的话)和要表达的意思。这就把语音识别问题转化为一个通信问题,而且进一步可以简化为用贝叶斯公式处理的数学问题。
一般情况下,一个句子中的每个字符都跟它前面的所有字符相关,这样公式中的条件概率计算就非常复杂,难以实现。为了简化问题,他做了两个假设:
1、 说话人说的句子是一个马尔科夫链,也就是说,句子中的每个字符都只由它前一个字符决定;
2、 独立输入假设,就是每个接受的字符信号只由对应的发送字符决定。
这样的简化看起来有点简单粗暴,每个字符在语义上都是和文章的其他部分相关的,怎么可能只跟它前一个字符相关呢?很多人不相信用这么简单的数学模型能解决复杂的语音识别、机器翻译等问题。其实不光是一般人,就连很多语言学家都曾质疑过这种方法的有效性。但事实证明,这个基于贝叶斯公式的统计语言模型比任何当时已知的借助某种规则的解决方法都有效。贾里尼克和贝克夫妇在七十年代分别独立提出用这个模型进行语音识别,八十年代微软公司用这个模型成功开发出第一个大词汇量连续语音识别系统。现在我们手机上的语音识别和语音输入功能都已经非常成熟而且好用了。
更加可贵的是,这种语音识别系统不但能够识别静态的词库,而且对词汇的动态变化具有很好的适应性,即使是新出现的词汇,只要这个词已经被大家高频使用,用于训练的数据量足够多,系统就能正确地识别。这反映出贝叶斯公式对现实变化的高度敏感,对增量信息有非常好的适应能力。
自然语言处理方面的成功开辟了一条全新的问题解决路径:
1、原来看起来非常复杂的问题可以用贝叶斯公式转化为简单的数学问题;
2、可以把贝叶斯公式和马尔科夫链结合以简化问题,使计算机能够方便求解;虽然我们不完全了解为什么这种看似粗暴的简化并不影响我们的研究过程,但从实践看来它非常有效;
3、将大量观测数据输入模型进行迭代——也就是对模型进行训练,我们就可以得到希望的结果。
随着计算能力的不断提高、大数据技术的发展,原来手工条件下看起来不可思议的进行模型训练的巨大工作量变得很容易实现,它们使贝叶斯公式巨大的实用价值体现出来。
二 经典统计学的困难和贝叶斯革命
1 经典统计学的困难
当贝叶斯方法在实际应用中不断证明自己的同时,经典统计学却遇到了困境。经典统计学比较适合于解决小型的问题,同时该方法要求我们获得足够多的样本数据,而且要求这些样本能够代表数据的整体特征。在处理涉及几个参数的问题时,它可以得心应手。但如果相对于问题的复杂程度,我们只掌握少量的信息时,经典统计学就显得力不从心了,原因就是数据的稀疏性问题。
都大数据时代了,还存在数据稀疏性问题吗?答案是肯定的。具体来说,一个取决于n个参数,并且每个参数只有两种表现(0或者1)的系统,共有2的n次方种现象。如果某类癌症的产生过程中有100个基因参与(这其实很保守了,人类总共有几万个基因),那么它有2的100次方种可能的基因图谱;根据采样定理进行估算,采用经典统计学方法至少需要获得1%-10%的样本才能确定其病因,也就是需要制作出数万亿亿亿个患有该疾病的病人的基因图谱!这不具备可操作性。所以用经典统计学方法无法解释由相互联系、错综复杂的原因(相关参数)所导致的现象。
2 贝叶斯网络带来工具革命
而目前的情况是,相对简单的问题已经解决得差不多了,剩下的都非常复杂。龙卷风的形成、星系的起源、致病基因、大脑的运作机制等,要揭示隐藏在这些问题背后的规律,就必须理解它们的成因网络,把错综复杂的事件梳理清楚。由于经典统计学失效,科学家别无选择,他们必须从众多可能奏效的法则中选择一些可以信任的,并以此为基础建立理论模型。为了能做出这样的选择,为了能在众多可能性中确定他们认为最为匹配的,过去,科学家多少是依靠直觉来弥补数据上的缺失和空白。而贝叶斯公式正好以严谨的数学形式帮他们实现了这一点。科学家把所有假设与已有知识、观测数据一起代入贝叶斯公式,就能得到明确的概率值。而要破译某种现象的成因网络,只需将公式本身也结成网络,即贝叶斯网络,它是贝叶斯公式和图论结合的产物。
网络化想法的提出也不是一帆风顺的。直到上世纪80年代,美国数学家朱迪亚·珀尔才证明,使用贝叶斯网络应该可以揭示复杂现象背后的成因。操作原理是这样的:如果我们不清楚一个现象的成因,首先根据我们认为最有可能的原因来建立一个模型;然后把每个可能的原因作为网络中的节点连接起来,根据已有的知识、我们的预判或者专家意见给每个连接分配一个概率值。接下来只需要向这个模型代入观测数据,通过网络节点间的贝叶斯公式重新计算出概率值。为每个新数据、每个连接重复这种计算,直到形成一个网络图,任意两个原因之间的连接都得到精确的概率值为止,就大功告成了。即使实验数据存在空白或者充斥噪声和干扰信息,不懈追寻各种现象发生原因的贝叶斯网络依然能够构建出各种复杂现象的模型。贝叶斯公式的价值在于,当观测数据不充分时,它可以将专家意见和原始数据进行综合,以弥补测量中的不足。我们的认知缺陷越大,贝叶斯公式的价值就越大。
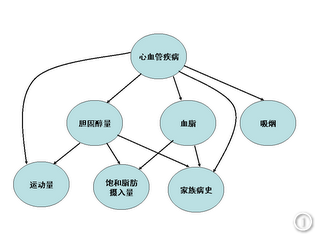
心血管疾病成因的贝叶斯网络
和前面提到的马尔可夫链类似,我们可以假设贝叶斯网络中每个节点的状态值取决于其前面的有限个状态。不同的是,贝叶斯网络比马尔可夫链灵活,它不受马尔可夫链的链状结构的约束,因此可以更准确地描述事件之间的相关性。可以说,马尔可夫链是贝叶斯网络的特例,而贝叶斯网络是马尔可夫链的推广,它给复杂问题提供了一个普适性的解决框架。
为了确定各个节点之间的相关性,需要用已知数据对贝叶斯网络进行迭代和训练。由于网络结构比较复杂,理论上,用现有的计算机是不可计算的(基于冯·诺依曼结构的计算机无法解决这种NP复杂度的问题,NP(Non-deterministic Polynomial)指用非确定机在多项式时间内可以解决的问题类)。但对于一些具体的应用,可以根据实际情况对网络结构(采用网络拓扑的图同构技术)和训练过程进行简化,使它在计算上可行。如果量子计算机开发成功,将能够完全解决其计算问题。这样,贝叶斯公式为科学家开辟的新路就完全打通了。
今天一场轰轰烈烈的“贝叶斯革命”正在发生:生物学家用贝叶斯公式研究基因的致病机制;基金经理用贝叶斯公式找到投资策略;互联网公司用贝叶斯公式改进搜索功能,帮助用户过滤垃圾邮件;大数据、人工智能和自然语言处理中都大量用到贝叶斯公式。既然在手工时代,我们无法预测到今天贝叶斯公式与计算机结合的威力,那么我们怎么能忽视贝叶斯网络与量子计算机结合可能蕴藏的巨大潜力呢?
3 人类大脑的构建方式?
贝叶斯公式不仅在自然科学领域掀起革命,它的应用范围也延伸到了关于人类行为和人类大脑活动的研究领域。教育学家突然意识到,学生的学习过程其实就是贝叶斯公式的运用;心理学家证明贝叶斯方法是儿童运用的唯一思考方法,其他方法他们似乎完全不会。进一步,心理学研究的成果使科学家思考人类的大脑结构是否就是一个贝叶斯网络。这个公式不仅是研究人类思维的工具,它可能就是大脑本身的构建方式。这个观点十分大胆,但获得越来越广泛的认可。因为贝叶斯公式是我们在没有充分或准确信息时最优的推理结构,为了提高生存效率,进化会向这个模式演进。贝叶斯公式突然渗透到一切科学领域,提供了通用的研究框架,这是十分罕见的事情。
人工智能近年来取得了长足的进步,但目前的人工智能通常需要从大量的数据中进行学习,而人类具有“仅从少量案例就形成概念”的能力,两者之间存在巨大差距。比如,尽管你这辈子只见过一个菠萝,但你一眼就能看出菠萝的特征,很快就能从一堆水果中认出菠萝来,甚至还能在纸上画出菠萝的简笔画,而目前的人工智能算法得看成千上万张菠萝的图片才能做到。
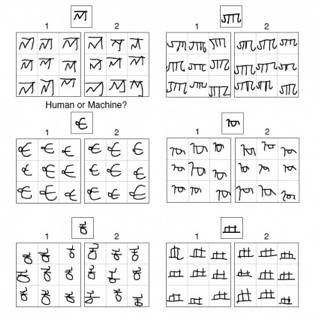
不过,这种情况或许已经开始改变了。2015年底,一篇人工智能论文登上了《 科学 》杂志的封面,为人们带来了人工智能领域的一个重大突破: 三名分别来自麻省理工学院、纽约大学和多伦多大学的研究者开发了一个“只看一眼就会写字”的计算机系统。只需向这个系统展示一个来自陌生文字系统的字符,它就能很快学到精髓,像人一样写出来,甚至还能写出其他类似的文字——更有甚者,它还通过了图灵测试,我们很难区分下图中的字符是人类还是机器的作品。这个系统采用的方法就是贝叶斯程序学习(Bayesian Program Learning)——一种基于贝叶斯公式的方法。这不但是人工智能领域的重大突破,而且为我们认识人脑的学习机制提供了重要参考。
三 理念的革命
这不仅仅是一场科学的革命,同样也是一场理念的革命。当科学不断强调其对世界认识的客观性时,贝叶斯公式却融入了主观性因素:它并不向我们表述世界,而是表述我们所掌握的知识和经验。这些带有观察者个人因素的知识是脱离研究现象本身的;而它在向我们描述外部现实世界的同时,也描述了观察者对现实的认知的缺陷。更重要的,它迫使我们认识到,科学理论和科学模型反映的是现实的心理意象,而不是现实本身。而现实为我们提供数据,以保证对现实的意象不会离现实本身太远。在寻找各种现象原因的同时,它也在规范着我们的思想。
四 贝叶斯公式这么牛,与我何干?
我们经常需要在信息不充分或者不准确的情况下进行判断和决策,一条街上哪个饭馆最靠谱?在自习室惊鸿一瞥的女神有没有男朋友?老公的公文包里发现一只口红,他有没有出轨?新开发的App应该等做得尽善尽美再发布,还是应该尽早发布,用互联网的力量帮助它完善?我应该选择哪个工作offer或者还是考公务员才能使自己的收益最大化?
贝叶斯公式为我们提供了一些决策原则:
•平时注意观察和思考,建立自己的思维框架,这样在面临选择时就容易形成一个接近实际情况的先验概率,这样经过少量的试错和纠错的迭代循环就可能得到理想的结果;在经过很多次选择和实践的历练后就能够形成自己的直觉,在面对陌生情况时,根据自己的经验和少量信息就能够快速地做出比较准确的判断。
•大数据时代获得信息的成本越来越低,社会也变得更加开放和包容,初始状态(先验概率)的重要性下降了,即使最初选择不理想,只要根据新情况不断进行调整,仍然可以取得成功。所以如果当下觉得很难做出选择,那就倾听内心的声音,让直觉来选择,这有利于治疗选择恐惧症。
以开发App的例子来说,先按照自己的想法弄个可用的原型出来,然后充分利用互联网的力量,让活跃的用户社区帮助它快速迭代,逐渐使它的功能和体验越来越好。
•对新鲜事物保持开放的心态,愿意根据新信息对自己的策略和行为进行调整。
“大胆假设,小心求证”,“不断试错,快速迭代”,这些都可以看成贝叶斯公式的不同表述。英国哲学家以赛亚·伯林(Isaish Berlin)曾经援引古希腊诗人的断简残片“狐狸多知而刺猬有一大知”,将人的策略分为狐狸和刺猬两类。刺猬用一个宏大的概念解释所有现象,而狐狸知道很多事情,用多元化的视角看待问题,它也愿意包容新的证据以使得自己的模型与之相适应。在这个快速变化的时代,固守一个不变的信条的刺猬很难适应环境的变化,而使用贝叶斯公式的灵活的狐狸才更容易生存。
参考文献
[1] 《新发现》杂志2013年2月:解密世界的方程式
[2] 吴军:《数学之美》
[3] 何帆:《先放一把火》
[4] 科学松鼠会:死理性派是怎么判断漂亮女孩是不是单身的?
[5] 统计之都创作小组:失联搜救中的统计数据分析
[6] 机器之心:《科学》封面重磅论文:人工智能终于能像人类一样学习







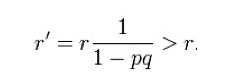
















 780
780

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








