神经网络一：介绍，示例，代码

最新推荐文章于 2022-07-11 23:57:11 发布

Bixiwen_liu

最新推荐文章于 2022-07-11 23:57:11 发布

阅读量1.2w

点赞数 2

分类专栏：深度学习文章标签：深度学习神经网络 python 斯坦福大学算法

本文链接：https://blog.csdn.net/Bixiwen_liu/article/details/52892141

版权

深度学习专栏收录该内容

33 篇文章 6 订阅

订阅专栏

有关神经网络的基本概述和神经网络模型，这里就不仔细介绍了。具体详细介绍可参见斯坦福大学的大牛Ng等人的介绍神经网络概述及其模型。这里主要介绍反向传导算法（Backpropagation Algorithm）的具体推导，以及神经网络有关的简单示例和相关Python代码。

一反向传导算法的推导过程

以人脑中的神经网络为启发，历史上出现过很多不同的版本，其中最著名的版本的算法是1980年的backpropagation。backpropagation被使用在多层向前神经网络上。

假设我们有一个固定样本集 $\textstyle \{ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) \}$ ，它包含 $\textstyle m$ 个样例。我们可以用批量梯度下降法来求解神经网络。具体来讲，对于单个样例 $\textstyle (x,y)$ ，其代价函数为：

$\begin{align}J(W,b; x,y) = \frac{1}{2} \left\| h_{W,b}(x) - y \right\|^2.\end{align}$ 其中y是真实标签值，h是预测值。

（注：这里相关变量取名是根据神经网络概述及其模型中的变量而来）

给定一个包含 $\textstyle m$ 个样例的数据集，我们可以定义整体代价函数为：

$\begin{align}J(W,b)&= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 \\&= \left[ \frac{1}{m} \sum_{i=1}^m \left( \frac{1}{2} \left\| h_{W,b}(x^{(i)}) - y^{(i)} \right\|^2 \right) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2\end{align}$

以上公式中的第一项 $\textstyle J(W,b)$ 是一个均方差项。第二项是一个正则化项，其目的是减小权重的幅度，防止过拟合。

梯度下降法中每一次迭代都按照如下公式对参数 $\textstyle W$ 和 $\textstyle b$ 进行更新：

$\begin{align}W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b)\end{align}$

其中 $\textstyle \alpha$ 是学习速率。其中关键步骤是计算偏导数。我们现在来讲一下反向传播算法，它是计算偏导数的一种有效方法。

首先来讲一下如何使用反向传播算法来计算 $\textstyle \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$ 和 $\textstyle \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y)$ ，这两项是单个样例 $\textstyle (x,y)$ 的代价函数 $\textstyle J(W,b;x,y)$ 的偏导数。一旦我们求出该偏导数，就可以推导出整体代价函数 $\textstyle J(W,b)$ 的偏导数：

$\begin{align}\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) &=\left[ \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \right] + \lambda W_{ij}^{(l)} \\\frac{\partial}{\partial b_{i}^{(l)}} J(W,b) &=\frac{1}{m}\sum_{i=1}^m \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x^{(i)}, y^{(i)})\end{align}$

反向传播算法的思路如下：给定一个样例 $\textstyle (x,y)$ ，我们首先进行“前向传导”运算，计算出网络中所有的激活值，包括 $\textstyle h_{W,b}(x)$ 的输出值。之后，针对第 $\textstyle l$ 层的每一个节点 $\textstyle i$ ，我们计算出其偏差 $\textstyle \delta^{(l)}_i$ ，该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点，我们可以直接算出网络产生的激活值与实际值之间的差距，我们将这个差距定义为 $\textstyle \delta^{(n_l)}_i$ （第 $\textstyle n_l$ 层表示输出层）。对于隐藏单元我们如何处理呢？我们将基于节点（译者注：第 $\textstyle l+1$ 层节点）残差的加权平均值计算 $\textstyle \delta^{(l)}_i$ ，这些节点以 $\textstyle a^{(l)}_i$ 作为输入。看到这里，首先有疑问的是残差是什么，怎么样得到残差？残差其实是对z的偏导数。对于一个神经元，它和上一层的很多神经元相连接，这些神经元的输出经过一个加权，然后相加的结果就是Z，也就是说这z是神经元的真正输入，残差表示的就是最终的代价函数对网络中的一个个神经元输入的偏导。残差体现的是对于代价的贡献的敏感程度，对于一个大的残差，稍微给点输入，就不行了，导致最后的loss很大。z又是关于权重w的函数，所以，按照链式法则可以传递到w对代价函数的贡献敏感度上。

下面将给出反向传导算法的细节：

进行前馈传导计算，利用前向传导公式，得到 $\textstyle L_2, L_3, \ldots$ 直到输出层 $\textstyle L_{n_l}$ 的激活值。
对于第 $\textstyle n_l$ 层（输出层）的每个输出单元 $\textstyle i$ ，我们根据以下公式计算残差：

$\begin{align}\delta^{(n_l)}_i &= \frac{\partial}{\partial z^{n_l}_i}J(W,b;x,y) = \frac{\partial}{\partial z^{n_l}_i}\frac{1}{2} \left\|y - h_{W,b}(x)\right\|^2 \\ &= \frac{\partial}{\partial z^{n_l}_i}\frac{1}{2} \sum_{j=1}^{S_{n_l}} (y_j-a_j^{(n_l)})^2 = \frac{\partial}{\partial z^{n_l}_i}\frac{1}{2} \sum_{j=1}^{S_{n_l}} (y_j-f(z_j^{(n_l)}))^2 \\ &= - (y_i - f(z_i^{(n_l)})) \cdot f'(z^{(n_l)}_i) = - (y_i - a^{(n_l)}_i) \cdot f'(z^{(n_l)}_i)\end{align}$

注：最终的目的还是求解 $\textstyle \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$ 和 $\textstyle \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y)$ ，这里转换了求解变量，最后根据偏导公式：来计算结果，对于b同样求得，见后面介绍。
对 $\textstyle l = n_l-1, n_l-2, n_l-3, \ldots, 2$ 的各个层，第 $\textstyle l$ 层的第 $\textstyle i$ 个节点的残差计算方法如下：

$\delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i)$

{译者注：

$\begin{align}\delta^{(n_l-1)}_i &=\frac{\partial}{\partial z^{n_l-1}_i}J(W,b;x,y) = \frac{\partial}{\partial z^{n_l-1}_i}\frac{1}{2} \left\|y - h_{W,b}(x)\right\|^2 = \frac{\partial}{\partial z^{n_l-1}_i}\frac{1}{2} \sum_{j=1}^{S_{n_l}}(y_j-a_j^{(n_l)})^2 \\&= \frac{1}{2} \sum_{j=1}^{S_{n_l}}\frac{\partial}{\partial z^{n_l-1}_i}(y_j-a_j^{(n_l)})^2 = \frac{1}{2} \sum_{j=1}^{S_{n_l}}\frac{\partial}{\partial z^{n_l-1}_i}(y_j-f(z_j^{(n_l)}))^2 \\&= \sum_{j=1}^{S_{n_l}}-(y_j-f(z_j^{(n_l)})) \cdot \frac{\partial}{\partial z_i^{(n_l-1)}}f(z_j^{(n_l)}) = \sum_{j=1}^{S_{n_l}}-(y_j-f(z_j^{(n_l)})) \cdot f'(z_j^{(n_l)}) \cdot \frac{\partial z_j^{(n_l)}}{\partial z_i^{(n_l-1)}} \\&= \sum_{j=1}^{S_{n_l}} \delta_j^{(n_l)} \cdot \frac{\partial z_j^{(n_l)}}{\partial z_i^{n_l-1}} = \sum_{j=1}^{S_{n_l}} \left(\delta_j^{(n_l)} \cdot \frac{\partial}{\partial z_i^{n_l-1}}\sum_{k=1}^{S_{n_l-1}}f(z_k^{n_l-1}) \cdot W_{jk}^{n_l-1}\right) \\&= \sum_{j=1}^{S_{n_l}} \delta_j^{(n_l)} \cdot W_{ji}^{n_l-1} \cdot f'(z_i^{n_l-1}) = \left(\sum_{j=1}^{S_{n_l}}W_{ji}^{n_l-1}\delta_j^{(n_l)}\right)f'(z_i^{n_l-1})\end{align}$

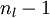将上式中的 $\textstyle n_l-1$ 与 $\textstyle n_l$ 的关系替换为 $\textstyle l$ 与 $\textstyle l+1$ 的关系，就可以得到：

$\delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i)$

以上逐次从后向前求导的过程即为“反向传导”的本意所在。 ]
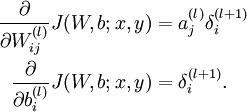
计算我们需要的偏导数，计算方法如下：根据公式，其中Z = Wa+b，得到： $\begin{align}\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}_j \delta_i^{(l+1)} \\\frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)}.\end{align}$
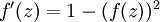如果选择 $\textstyle f(z) = 1/(1+\exp(-z))$ ，也就是sigmoid函数，那么它的导数就是 $\textstyle f'(z) = f(z) (1-f(z))$ ；如果选择tanh函数，那它的导数就是 $\textstyle f'(z) = 1- (f(z))^2$ 。

那么，反向传播算法可表示为以下几个步骤：

进行前馈传导计算，利用前向传导公式，得到 $\textstyle L_2, L_3, \ldots$ 直到输出层 $\textstyle L_{n_l}$ 的激活值。
对输出层（第 $\textstyle n_l$ 层），计算：

$\begin{align}\delta^{(n_l)}= - (y - a^{(n_l)}) \bullet f'(z^{(n_l)})\end{align}$
对于 $\textstyle l = n_l-1, n_l-2, n_l-3, \ldots, 2$ 的各层，计算：

$\begin{align}\delta^{(l)} = \left((W^{(l)})^T \delta^{(l+1)}\right) \bullet f'(z^{(l)})\end{align}$
计算最终需要的偏导数值：

$\begin{align}\nabla_{W^{(l)}} J(W,b;x,y) &= \delta^{(l+1)} (a^{(l)})^T, \\\nabla_{b^{(l)}} J(W,b;x,y) &= \delta^{(l+1)}.\end{align}$

5.最后不断更新：

$\begin{align}W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b)\end{align}$

更新的终止条件有：

1）：权重的更新低于某个阈值；

2）：预测的错误率低于某个阈值；

3）：达到一定的循环次数，退出循环

二简单示例

如图，这是示例的神经网络模型和具体的一些值，其中权重w的值时随机初始化的（不相等即可）。

根据公式

$\textstyle z_i^{(2)} = \sum_{j=1}^n W^{(1)}_{ij} x_j + b^{(1)}_i$ 和 $\textstyle a^{(l)}_i = f(z^{(l)}_i)$ 算出相应的激活值为;Ij = Zi,Oj = ai

注：这里选择 $\textstyle f(z) = 1/(1+\exp(-z))$ ，也就是sigmoid函数，那么它的导数就是 $\textstyle f'(z) = f(z) (1-f(z))$ 。

下面开始用反向传导算法，更新W和b的值：这里的Errj = δ。先算出每一层的偏差：

根据公式

$\begin{align}\nabla_{W^{(l)}} J(W,b;x,y) &= \delta^{(l+1)} (a^{(l)})^T, \\\nabla_{b^{(l)}} J(W,b;x,y) &= \delta^{(l+1)}.\end{align}$ $\begin{align}W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b)\end{align}$

这里选择的步长（α）为：0.9。最后更新算出所有的权重W和b的值：

三 Python示例代码

<pre name="code" class="python">import numpy as np

#下面定义所使用的激活函数及其相应的导数的函数
#这里使用了正切函数和logistic函数
def tanh(x):
    return np.tanh(x)

def tanh_deriv(x):
    return 1.0-np.tanh(x)*np.tanh(x)

def logistic(x):
    return 1/(1+np.exp(-x))

def logistic_deriv(x):
    return logistic(x)*(1-logistic(x))


class NeuralNetwork:#定义一个类
    def __init__(self, layers, activation='tanh'):

        if activation == 'logistic':
            self.activation = logistic
            self.activation_deriv = logistic_deriv
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_deriv = tanh_deriv
        #对权重初始化。对每一层的权重都要初始化
        self.weights = []
        for i in range(1,len(layers)-1):
            #对每一层的权重都要初始化初始值范围在-0.25~0.25之间，然后保存在weight中
            self.weights.append((2*np.random.random((layers[i-1]+1,layers[i]+1))-1)*0.25)
            self.weights.append((2*np.random.random((layers[i]+1,layers[i+1]))-1)*0.25)

    def fit(self, X, y, learning_rate=0.2, epochs=10000):#默认学习率即步长为0.2，循环最多的次数为1000
        X = np.atleast_2d(X)#判断输入训练集是否为二维
        temp = np.ones([X.shape[0],X.shape[1]+1])#列加1是因为最后一列要存入标签分类，这里标签都为1
        temp[:,0:-1] = X
        X = temp
        y = np.array(y)#训练真实值

        for k in range(epochs):#循环
            i = np.random.randint(X.shape[0])#随机选取训练集中的一个
            a = [X[i]]
            #计算激活值
            for l in range(len(self.weights)):
                a.append(self.activation(np.dot(a[l], self.weights[l])))

            error = y[i] - a[-1]#计算偏差
            deltas = [error*self.activation_deriv(a[-1])]#输出层误差
            #下面计算隐藏层     
            for l in range(len(a)-2,0,-1):
                deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
            deltas.reverse()
            #下面开始更新权重和偏向
            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)
    #预测函数
    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0]+1)
        temp[0:-1] = x
        a = temp
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        for i in range(a):
            if  a[i]>0.5:
                a[i] = 1
            else:
                a[i] = 0 
        return a

下面是训练集和测试集：

import numpy as np

nn = NeuralNetwork([2,2,1],'tanh')
X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([0,1,1,0])
nn.fit(X, y)
for i in [[0,0],[0,1],[1,0],[1,1]]:
    print(i, nn.predict(i))

结果为：

([0, 0], array([ 0.0171341]))
([0, 1], array([ 0.99848996]))
([1, 0], array([ 0.99852684]))
([1, 1], array([ 0.04127888]))

可以设置阈值，比如当测试值>0.5是结果为1，否则为0。这样测试集结果与训练集相同，即全部正确