基于一致性原理的时间协同制导及其Matlab仿真

来源：https://maiya.fan/blog?id=658ec46390d3d1241da10728

引言

本文给出了多智能体系统的一致性理论、多弹剩余时间协同制导律及其Matlab代码。

多智能体系统的一致性原理

系统模型

考虑连续时间内由n个智能体构成的n阶多智能体系统，每个智能体的动力学模型为：

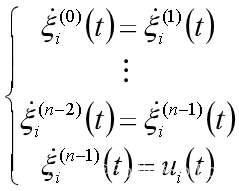
式中t——时间；
——第i个智能体的状态，表示k阶导数，k = 0, 1,…, n-1；
ut——第i个智能体的控制输入。

如果在任意初始条件下，控制算法能够使得多智能体系统的状态满足

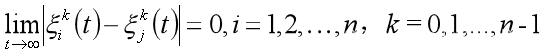
则称多智能体系统的状态在控制算法的作用下能够渐近的达到一致。

如果在任意初始条件下，存在常数，控制算法ut能够使得

则称领导-跟随多智能体系统的状态在控制算法的作用下能够在有限时间内达到一致。

经典一致性控制算法

经典一致性控制算法：

式中N——智能体i的邻居集合；
a——固定拓扑结构下智能体i的邻接矩阵元素；
γ——智能体i的控制增益；
α——符号函数的幂指数；
β——相对信息的反馈增益。

代码及仿真结果

核心代码（全部代码在文末）：

function [output] = control(state_self, state_com)
%CONTROL 根据自身信息和接收到的状态计算出控制量
%   输入：自身状态，接收到的状态
%   输出：控制量
% 控制增益,行表示不同状态，列表示不同节点
gama = [4, 4, 4, 4, 4;
	    8, 8, 8, 8, 8;
        8, 8, 8, 8, 8];
% 符号函数的幂指数
alpha = [0.8, 0.8, 0.8, 0.8, 0.8;
         0.67, 0.67, 0.67, 0.67, 0.67;
         0.57, 0.57, 0.57, 0.57, 0.57];
%%
num_node = size(state_self,2);
output = zeros(1,num_node);
% 接受节点序号
for i =1:num_node
    for cou_state = 1:size(state_self,1)
        state_temp = 0;
        % 发送节点序号
        for j =1:size(state_com{1,i},2)
            state_temp = state_temp+ state_com{1,i}(cou_state,j)-state_self(cou_state,i);
        end
        output(1,i) = output(1,i) + ...
            gama(cou_state,i)*sig(state_temp,alpha(cou_state,i));
    end
end
end

结果展示：
一阶：

二阶

三阶

基于一致性原理的时间协同制导律

系统模型

在三维协同制导空间中，第i个飞行器的加速度在视线系三个轴的分量为
，目标加速度在视线系三个轴的分量为。与平面相对运动模型类似，定义如下三维空间内飞行器和目标的相对速度矢量表达式。

其中 R ——第i个飞行器与目标距离；
——第i个飞行器的视线在惯性系中的高低角；
——第i个飞行器的视线在惯性系中的偏角；

VR——第i个飞行器视线系中x轴的速度；
——第i个飞行器视线系中y轴速度；
Vq——第i个飞行器视线系中z轴速度。
求导，可得

其中 ——在惯性系中相对时间的导数；
——在视线系中相对时间的导数；
——视线系相对于惯性系的旋转角速度；
w——目标加速度在视线系各轴的分量；
u——第i个飞行器的加速度在视线系各轴的分量。
可以得出

带入，得

整理可得

与平面的协同制导问题一样，设计三维空间协同制导律的关键是首先通过和使得视线角速率制导过程中使得视线角速率和趋近于零，从而实现准平行接近；然后在视线稳定的情况下利用调整飞行器的剩余飞行时间，实现多个飞行器的时间一致。

基于一致性原理的剩余飞行时间控制方法

本节给出视线方向控制量的设计方法。根据多智能体一阶积分系统有限时间一致性算法，给出三维空间内协同制导律视线方向控制定理。
定义函数
符号函数定义为

假设系统的齐次度为k，如果原点是渐进稳定的，并且k>0，那么系统的原点是有限时间稳定点。
利用领导-跟随多智能体一致性理论和有限时间控制方法，当多飞行器系统的通信拓扑是连通时，为第i个跟随飞行器设计如下控制算法:

可以使系统的状态在有限时间内达到一致。
用替换式中的，可以得到如下有限时间一致性算法:

令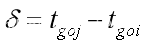, 可以写为

代码及仿真结果

核心代码（全部代码在文末）：

function [ u ] = control( status, other_missiles, t )
% 控制器参数
n = 3;
beta = 2;
eta = 0.7;
%%
u = zeros(3,1);
sum_error = 0;
for cou_other_missile = 1:size(other_missiles,2)
    sum_error = sum_error + other_missiles(1, cou_other_missile) /...
        other_missiles(4, cou_other_missile) - status(1, 1) / status(4, 1);
end
% 固定数17最合适或者直接使用t
u(1,1) = min([max([t * sig(sum_error, eta),-200]),200]); 
u(2,1) = min([max([-n * status(4, 1) * status(6, 1) + ...
    beta * sig(status(6, 1), eta),-200]),200]); 
u(3,1) = min([max([n * status(4, 1) * status(5, 1)-...
    beta * sig(status(5, 1), eta),-200]),200]); 
end

结果展示：

完整代码分为多个文件，数量较多，无法放在文章中。完整代码在下方：