图解LightGBM直方图算法、单边梯度采样算法（GOSS）

我近期研究了各种树模型，在理解LightGBM的直方图、GOSS单边梯度采样环节时都有些困难。我在网上找了很多资料，但大部分以文字为主，且非常抽象，理解起来十分困难。

因此我想通过画图、画表、举例子的方式，具体解释一下LightGBM的直方图算法和GOSS算法。

本文旨在以图表化的方式展现直方图算法和GOSS算法的具体过程，因此不涉及任何数学推导和代码内容。如果有小伙伴对梯度提升树、xgboost、LightGBM的概念还比较陌生，建议先补充相关知识。

假设现在有这么一个案例：在第n次生成弱学习器时，样本如下，

本文将围绕这个案例展开

直方图算法

在什么时间点生成直方图？

首先明确，这个过程发生在遍历每个特征时。也就是说，在构建每一轮的决策树时，每个特征列都会生成1张直方图。

对本文的案例而言，此时模型开始第n次生成弱学习器。

第一步需要做什么？是找到第一个分割点。

如何找到第一个分裂点？循环x1和x2，看看它们内部哪一个分割点的增益最大。

万一x1和x2数据量很大怎么办？如果有100万个样本点，那么x1和x2将会产生（100万+100万-2）个分割点，这显然是极其消耗算力的。因此采用直方图算法来加速这个过程。但是由于直方图带来的精度丢失，可能无法求解出数学意义上的最优解，所以本质上是牺牲精度换取效率。

 

直方图都存储了什么信息？

有一些回答说：样本点数量 + 样本点的梯度和

但我经过反复实验，认为还必须储存样本点的id，或者索引、指针之类能够回溯到该样本点本身的信息，才能够实现直方图的加减。

对本文的案例而言，可以把原数据转化成这样存储：

注意，这个过程并不是排序，而是：

1. 创建若干个“框”，例如我为x2创建了三个“框”，分别是[3,4] , [5,7], [8-10]。

2. 循环x2的8个样本点，判断每个样本点属于哪一个“框”。

3. 对每个特征都进行如此的操作。

整个过程并不涉及排序，因此比xgboost预排序的时间复杂度小很多。

 

如何实现直方图作差加速？

 图片来源：(十)LightGBM的原理、具体实例、代码实现 - 知乎

这里的关键问题就在于x2的左子节点直方图如何得到。这也是我为什么认为直方图还需要额外存储样本点的id的原因。

还是之前的例子：

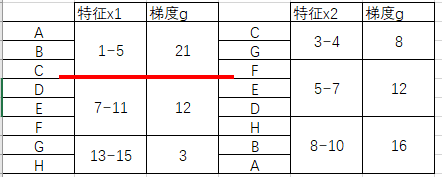
假设我以这条红线做分割，于是可以得到x1的左右两个节点：

但是要得到x2的左节点就没有那么直接了：我首先需要回溯x1特征属于左节点的样本点ABC，再到原始表格中回溯它们的x2特征，再查看这个特征属于x2直方图中的哪一个区间。

以上过程成立的基本条件是：我能够通过x1直方图回溯到样本点ABC，因此我认为直方图需要存储特征所对应的样本点信息。

当我找到ABC的x2特征后，我就可以填充x2直方图：

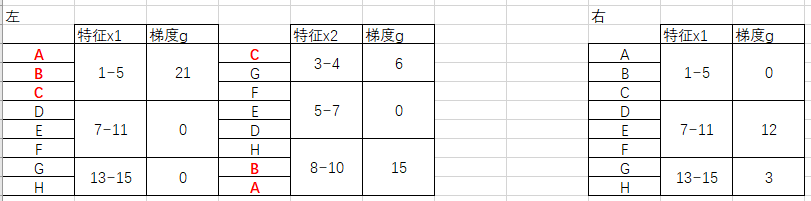
然后就可以应用直方图作差，直接得出右子节点的x2直方图：

但是，我并没有在其它的论坛、博客、论文中找到与我上述结论类似的结论，我只是模拟真实过程进行了一步步的推导得出的合理推测。因此，或许会存在不严谨的地方，希望各位小伙伴指正。当然，如果有时间我会啃一下github的源码。

 

单边梯度采样算法（GOSS）

在什么时间点进行单边梯度采样？

首先明确，这个过程发生在构建决策树前。也就是说，我这个模型生成了n颗决策树，就意味着我进行了n次GOSS过程。即每生成1个弱学习器，就进行一次GOSS过程。

还是上述的例子，此时假设我进入第n轮决策树的构建。

根据梯度从大到小，可以理解为样本点的重要性也在依次递减。我选择前50%作为大梯度样本，然后在剩余的样本中，抽取整体数量的25%作为小梯度样本：

如此，我选中了ABCD+FG作为我本轮的训练集。

膨胀系数？

为了平衡采样之后的不均匀分布的样本，我们需要为小梯度样本乘上一个膨胀系数。

膨胀系数 = (1-top_rate)/other_rate。这里即为(1-50%)/25% = 2

至此，我本轮的训练集构建完成。在本轮的增益计算中，我需要使用膨胀后的梯度gg。

此轮过后，样本点E和H将不会再出现在训练集中，因为它们既然不参与本轮训练，那么也就不产生y_hat，因此也就无法再计算梯度，所以也就无法再去拟合负梯度。

这个goss过程，随着每轮决策树的构建，会使得用于训练的样本会越来越少，这表示模型越来越注重梯度更大的样本（梯度越大，对目标函数的影响就越大），这个操作其实跟adaboost中为样本点加权的操作的道理是相通的。