LeGO-LOAM分析之特征提取（二）

最新推荐文章于 2024-06-21 17:17:24 发布

Philtell

最新推荐文章于 2024-06-21 17:17:24 发布

阅读量2.2k

点赞数 5

分类专栏： slam 文章标签：自动驾驶

原文链接：https://zhuanlan.zhihu.com/p/384902839

版权

slam 专栏收录该内容

33 篇文章

订阅专栏

转载地址：https://zhuanlan.zhihu.com/p/384902839
接着上一章的分析，LeGO-LOAM进行点云分割之后，接着会对分割后的点云进行特征提取，下面我们首先回顾下点云分割的过程，然后开始分析特征提取。

点云分割

LeGO-LOAM首先进行地面分割，找到地面之后，对地面之上的点进行聚类。聚类的算法如下图，主要是根据斜率对物体做切割，最后得到地面和分割后的点云。上述步骤的关键是要理解如何进行地面分割和点云分割。

在这里插入图片描述

特征提取

点云分割完成之后，接下来对分割后的点云提取特征，提取的特征的目的是进行点云配准，从而得出当前位姿。

LeGO-LOAM的特征提取和点云配准的过程都在LeGO-LOAM\src\featureAssociation.cpp中。下面我们开始逐步分析代码。

和点云分割一样，特征提取也是单独的ROS执行程序，函数入口在main函数中。也是在构造函数FeatureAssociation()中申明订阅消息和回调函数，与点云分割不同的是，在主函数中通过循环调用runFeatureAssociation来提取特征和特征匹配。

主函数

总结一下，LeGO-LOAM特征提取的实现分为2个步骤

消息订阅和回调，在构造函数中申明。
接收到消息之后，循环调用runFeatureAssociation提取特征，并且进行特征匹配，获取位姿。
也就是说主要的执行步骤在runFeatureAssociation中。

int main(int argc, char** argv)
{
    ros::init(argc, argv, "lego_loam");

    ROS_INFO("\033[1;32m---->\033[0m Feature Association Started.");
    // 1. 在构造函数中订阅消息和消息回调函数
    FeatureAssociation FA;

    ros::Rate rate(200);
    // 2. 循环调用runFeatureAssociation，函数的主流程所在
    while (ros::ok())
    {
        ros::spinOnce();

        FA.runFeatureAssociation();

        rate.sleep();
    }
    
    ros::spin();
    return 0;
}

接下来我们先看消息回调，然后再看主流程runFeatureAssociation。

消息回调

消息回调主要是接收上一个步骤（点云分割）中分割好的点云消息。

  FeatureAssociation():
        nh("~")
        {
        // 1. 接收消息，上一步分割好的点云
        subLaserCloud = nh.subscribe<sensor_msgs::PointCloud2>("/segmented_cloud", 1, &FeatureAssociation::laserCloudHandler, this);
        subLaserCloudInfo = nh.subscribe<cloud_msgs::cloud_info>("/segmented_cloud_info", 1, &FeatureAssociation::laserCloudInfoHandler, this);
        subOutlierCloud = nh.subscribe<sensor_msgs::PointCloud2>("/outlier_cloud", 1, &FeatureAssociation::outlierCloudHandler, this);
        subImu = nh.subscribe<sensor_msgs::Imu>(imuTopic, 50, &FeatureAssociation::imuHandler, this);
        // 2. 发布消息
        pubCornerPointsSharp = nh.advertise<sensor_msgs::PointCloud2>("/laser_cloud_sharp", 1);
        pubCornerPointsLessSharp = nh.advertise<sensor_msgs::PointCloud2>("/laser_cloud_less_sharp", 1);
        pubSurfPointsFlat = nh.advertise<sensor_msgs::PointCloud2>("/laser_cloud_flat", 1);
        pubSurfPointsLessFlat = nh.advertise<sensor_msgs::PointCloud2>("/laser_cloud_less_flat", 1);

        pubLaserCloudCornerLast = nh.advertise<sensor_msgs::PointCloud2>("/laser_cloud_corner_last", 2);
        pubLaserCloudSurfLast = nh.advertise<sensor_msgs::PointCloud2>("/laser_cloud_surf_last", 2);
        pubOutlierCloudLast = nh.advertise<sensor_msgs::PointCloud2>("/outlier_cloud_last", 2);
        pubLaserOdometry = nh.advertise<nav_msgs::Odometry> ("/laser_odom_to_init", 5);
        
        initializationValue();
    }

下面我们具体看这4个消息

segmented_cloud 分割好的点云。
segmented_cloud_info 分割好的点云，和segmented_cloud的区别是，segmented_cloud_info的强度信息是距离，而segmented_cloud的是range image的行列信息。
outlier_cloud 离群点，也就是分割失败的点。
imuTopic 接收imu的消息。
在理解了上述4个消息之后，我们分别看下他们的回调，点云消息的回调主要是把ROS的消息转换为点云，IMU的回调主要是把IMU的消息放入buffer中。

  // 1. 接收"/segmented_cloud"消息，保存到segmentedCloud
    void laserCloudHandler(const sensor_msgs::PointCloud2ConstPtr& laserCloudMsg){

        cloudHeader = laserCloudMsg->header;

        timeScanCur = cloudHeader.stamp.toSec();
        timeNewSegmentedCloud = timeScanCur;

        segmentedCloud->clear();
        pcl::fromROSMsg(*laserCloudMsg, *segmentedCloud);

        newSegmentedCloud = true;
    }
    // 2. 接收"/outlier_cloud"消息，保存到outlierCloud
    void outlierCloudHandler(const sensor_msgs::PointCloud2ConstPtr& msgIn){

        timeNewOutlierCloud = msgIn->header.stamp.toSec();

        outlierCloud->clear();
        pcl::fromROSMsg(*msgIn, *outlierCloud);

        newOutlierCloud = true;
    }
    // 3. 接收"/segmented_cloud_info"消息，并且保存到segInfo中
    // 注意这里没有转换为PCL点云，而是直接保存的消息cloud_msgs::cloud_info segInfo
    void laserCloudInfoHandler(const cloud_msgs::cloud_infoConstPtr& msgIn)
    {
        timeNewSegmentedCloudInfo = msgIn->header.stamp.toSec();
        segInfo = *msgIn;
        newSegmentedCloudInfo = true;
    }

接下来看IMU回调函数，接收到IMU消息之后保存到数组。IMU还做了一些角度的转换，这里暂时不做深究，后面有时间再补充。

void imuHandler(const sensor_msgs::Imu::ConstPtr& imuIn)
{
    double roll, pitch, yaw;
    tf::Quaternion orientation;
    tf::quaternionMsgToTF(imuIn->orientation, orientation);
    tf::Matrix3x3(orientation).getRPY(roll, pitch, yaw);

    float accX = imuIn->linear_acceleration.y - sin(roll) * cos(pitch) * 9.81;
    float accY = imuIn->linear_acceleration.z - cos(roll) * cos(pitch) * 9.81;
    float accZ = imuIn->linear_acceleration.x + sin(pitch) * 9.81;

    imuPointerLast = (imuPointerLast + 1) % imuQueLength;

    imuTime[imuPointerLast] = imuIn->header.stamp.toSec();

    imuRoll[imuPointerLast] = roll;
    imuPitch[imuPointerLast] = pitch;
    imuYaw[imuPointerLast] = yaw;

    imuAccX[imuPointerLast] = accX;
    imuAccY[imuPointerLast] = accY;
    imuAccZ[imuPointerLast] = accZ;

    imuAngularVeloX[imuPointerLast] = imuIn->angular_velocity.x;
    imuAngularVeloY[imuPointerLast] = imuIn->angular_velocity.y;
    imuAngularVeloZ[imuPointerLast] = imuIn->angular_velocity.z;

    AccumulateIMUShiftAndRotation();
}

接着分别对位置、速度和角度做积分，计算出当前的位置、速度和角度。

void AccumulateIMUShiftAndRotation()
    {
        float roll = imuRoll[imuPointerLast];
        float pitch = imuPitch[imuPointerLast];
        float yaw = imuYaw[imuPointerLast];
        float accX = imuAccX[imuPointerLast];
        float accY = imuAccY[imuPointerLast];
        float accZ = imuAccZ[imuPointerLast];

        float x1 = cos(roll) * accX - sin(roll) * accY;
        float y1 = sin(roll) * accX + cos(roll) * accY;
        float z1 = accZ;

        float x2 = x1;
        float y2 = cos(pitch) * y1 - sin(pitch) * z1;
        float z2 = sin(pitch) * y1 + cos(pitch) * z1;

        accX = cos(yaw) * x2 + sin(yaw) * z2;
        accY = y2;
        accZ = -sin(yaw) * x2 + cos(yaw) * z2;

        int imuPointerBack = (imuPointerLast + imuQueLength - 1) % imuQueLength;
        double timeDiff = imuTime[imuPointerLast] - imuTime[imuPointerBack];
        if (timeDiff < scanPeriod) {
            // 1. 位置积分
            imuShiftX[imuPointerLast] = imuShiftX[imuPointerBack] + imuVeloX[imuPointerBack] * timeDiff + accX * timeDiff * timeDiff / 2;
            imuShiftY[imuPointerLast] = imuShiftY[imuPointerBack] + imuVeloY[imuPointerBack] * timeDiff + accY * timeDiff * timeDiff / 2;
            imuShiftZ[imuPointerLast] = imuShiftZ[imuPointerBack] + imuVeloZ[imuPointerBack] * timeDiff + accZ * timeDiff * timeDiff / 2;
            // 2. 速度积分
            imuVeloX[imuPointerLast] = imuVeloX[imuPointerBack] + accX * timeDiff;
            imuVeloY[imuPointerLast] = imuVeloY[imuPointerBack] + accY * timeDiff;
            imuVeloZ[imuPointerLast] = imuVeloZ[imuPointerBack] + accZ * timeDiff;
            // 3. 角度积分
            imuAngularRotationX[imuPointerLast] = imuAngularRotationX[imuPointerBack] + imuAngularVeloX[imuPointerBack] * timeDiff;
            imuAngularRotationY[imuPointerLast] = imuAngularRotationY[imuPointerBack] + imuAngularVeloY[imuPointerBack] * timeDiff;
            imuAngularRotationZ[imuPointerLast] = imuAngularRotationZ[imuPointerBack] + imuAngularVeloZ[imuPointerBack] * timeDiff;
        }
    }

以上就是消息接收过程，接下来我们看主流程runFeatureAssociation。

主流程（runFeatureAssociation）

主函数的流程非常清晰，总共分为2个大的步骤

特征提取，提取线特征和面特征
特征匹配，利用最小二乘法，获取当前最优的位姿

void runFeatureAssociation()
    {
        // 0. 判断是否接收到消息，并且消息延迟小于0.05s
        if (newSegmentedCloud && newSegmentedCloudInfo && newOutlierCloud &&
            std::abs(timeNewSegmentedCloudInfo - timeNewSegmentedCloud) < 0.05 &&
            std::abs(timeNewOutlierCloud - timeNewSegmentedCloud) < 0.05){

            newSegmentedCloud = false;
            newSegmentedCloudInfo = false;
            newOutlierCloud = false;
        }else{
            return;
        }
       
        // 1. Feature Extraction（特征提取）
        // 1.1 点云运动补偿
        adjustDistortion();
        // 1.2 计算平滑度
        calculateSmoothness();
        // 1.3 标记遮挡点
        markOccludedPoints();
        // 1.4 提取特征
        extractFeatures();
        // 1.5 发布点云
        publishCloud(); // cloud for visualization
	

	// 2. Feature Association（特征匹配）
        if (!systemInitedLM) {
            // 2.1 检查系统初始化
            checkSystemInitialization();
            return;
        }
        // 2.2 更新初始猜测位置
        updateInitialGuess();
        // 2.3 特征匹配，输出Transformation
        updateTransformation();
        // 2.4 变换坐标Transformation
        integrateTransformation();
        // 2.5 发布雷达里程计
        publishOdometry();
        // 2.6 发布点云用于建图
        publishCloudsLast(); // cloud to mapOptimization
    }

特征提取的过程：先对点云进行畸变校正（运动补偿），接着计算点的平滑程度，然后按照平滑度排序，如果是不平滑的点，则选为线特征（柱子或者墙壁的棱角），如果是平滑的点，则选为面特征（地面，墙面等平面）。同时为了避免选择的特征过于集中在同一个地方，会把360°方向切分为6个区域，每个区域平均选择2个线特征和4个面特征。
在这里插入图片描述

运动补偿

由于Lidar扫描过程中，小车在运动，这样对于同一个物体可能会导致出现畸变的情况，需要根据小车的位移对点云进行校正。

计算平滑度

平滑度的计算是取当前点的左边5个点和右边5个点和当前点的深度差值，然后求平方。而论文中的计算方法和代码中的不一样，论文中是取深度差的平均值，然后除以自身的模，也就是说论文中的曲率和尺度无关，不管当前点离lidar近还是远，只要曲率超过一定的值就可以，同时在仿真环境也可以解决尺度的问题，而代码中直接取得是绝对大小。

在这里插入图片描述

论文中S为点集， $r_j$ 表示S中不等于i的点的深度， $r_i$ 则表示自身的深度。

void calculateSmoothness()
{
    int cloudSize = segmentedCloud->points.size();
    for (int i = 5; i < cloudSize - 5; i++) {
        // 1. 计算相邻10个点深度差的和
        float diffRange = segInfo.segmentedCloudRange[i-5] + segInfo.segmentedCloudRange[i-4]
                        + segInfo.segmentedCloudRange[i-3] + segInfo.segmentedCloudRange[i-2]
                        + segInfo.segmentedCloudRange[i-1] - segInfo.segmentedCloudRange[i] * 10
                        + segInfo.segmentedCloudRange[i+1] + segInfo.segmentedCloudRange[i+2]
                        + segInfo.segmentedCloudRange[i+3] + segInfo.segmentedCloudRange[i+4]
                        + segInfo.segmentedCloudRange[i+5];            
        // 2. 取平方
        cloudCurvature[i] = diffRange*diffRange;

        cloudNeighborPicked[i] = 0;
        cloudLabel[i] = 0;
        // 3. 保存曲率，保存索引
        cloudSmoothness[i].value = cloudCurvature[i];
        cloudSmoothness[i].ind = i;
    }
}

为什么cloudSmoothness也要保存索引，是因为后面会对cloudSmoothness数组排序，排序之后数组原来的索引就乱了，保存索引之后就知道点在原始点云中的索引(index)是多少。

标记遮挡点

计算完平滑度之后，我们首先标记一下效果不是非常理想的点，方便后续处理。那么什么是效果不好的点呢？在LOAM论文中有以下2种情况。
在这里插入图片描述

图(a) 中有2个特征点A和B，但B的方向和激光雷达的光束几乎平行，因此移动的过程中很可能丢失，所以尽量不要选择B。
图(b)中有2个特征点A和B，但A后续可能会被B遮挡了，橙色线标识的部分。所以A也尽量要排除。

实际上图(a)中所说的情况在LOAM中存在，而在LeGO-LOAM中可能不存在，因为LOAM没有做分割，而LeGO-LOAM做过分割，已经去除掉斜率比较大的点了，所以代码中我没有找到图(a)的情况。

void markOccludedPoints()
    {
        int cloudSize = segmentedCloud->points.size();

        for (int i = 5; i < cloudSize - 6; ++i){

            float depth1 = segInfo.segmentedCloudRange[i];
            float depth2 = segInfo.segmentedCloudRange[i+1];
            int columnDiff = std::abs(int(segInfo.segmentedCloudColInd[i+1] - segInfo.segmentedCloudColInd[i]));
            // 1. 标记有遮挡的点
            if (columnDiff < 10){

                if (depth1 - depth2 > 0.3){
                    cloudNeighborPicked[i - 5] = 1;
                    cloudNeighborPicked[i - 4] = 1;
                    cloudNeighborPicked[i - 3] = 1;
                    cloudNeighborPicked[i - 2] = 1;
                    cloudNeighborPicked[i - 1] = 1;
                    cloudNeighborPicked[i] = 1;
                }else if (depth2 - depth1 > 0.3){
                    cloudNeighborPicked[i + 1] = 1;
                    cloudNeighborPicked[i + 2] = 1;
                    cloudNeighborPicked[i + 3] = 1;
                    cloudNeighborPicked[i + 4] = 1;
                    cloudNeighborPicked[i + 5] = 1;
                    cloudNeighborPicked[i + 6] = 1;
                }
            }

            float diff1 = std::abs(float(segInfo.segmentedCloudRange[i-1] - segInfo.segmentedCloudRange[i]));
            float diff2 = std::abs(float(segInfo.segmentedCloudRange[i+1] - segInfo.segmentedCloudRange[i]));
            // 2. 这里我理解是标记离群点，也就是和周围点相差比较大的点。
            if (diff1 > 0.02 * segInfo.segmentedCloudRange[i] && diff2 > 0.02 * segInfo.segmentedCloudRange[i])
                cloudNeighborPicked[i] = 1;
        }
    }

提取特征

接下来就进行提取特征的操作了，提取的特征分为2类，一类是曲率比较大的线特征，一类是曲率比较小的面特征。

提取的方法是把平面划分为6等分，也就是6个方向（LOAM中为前、后、左、右4个方向），根据上述计算好的曲率进行排序，然后每个方向最多选择2个线特征和4个面特征，如果超过则跳过，在下一个方向上继续选择。如果一个点已经被选择为特征点，那么它的相邻点会被标记，不允许被选为特征了。

void extractFeatures()
    {
        cornerPointsSharp->clear();
        cornerPointsLessSharp->clear();
        surfPointsFlat->clear();
        surfPointsLessFlat->clear();

        for (int i = 0; i < N_SCAN; i++) {

            surfPointsLessFlatScan->clear();
            // 1. 分为6个方向，每个方向分别选择线特征和面特征
            for (int j = 0; j < 6; j++) {
                int sp = (segInfo.startRingIndex[i] * (6 - j)    + segInfo.endRingIndex[i] * j) / 6;
                int ep = (segInfo.startRingIndex[i] * (5 - j)    + segInfo.endRingIndex[i] * (j + 1)) / 6 - 1;

                if (sp >= ep)
                    continue;
                // 2. 根据曲率排序
                std::sort(cloudSmoothness.begin()+sp, cloudSmoothness.begin()+ep, by_value());

                int largestPickedNum = 0;
                // 3. 选择线特征，不为地面，segInfo.segmentedCloudGroundFlag[ind] == false
                for (int k = ep; k >= sp; k--) {
                    int ind = cloudSmoothness[k].ind;
                    if (cloudNeighborPicked[ind] == 0 &&
                        cloudCurvature[ind] > edgeThreshold &&
                        segInfo.segmentedCloudGroundFlag[ind] == false) {
                    
                        largestPickedNum++;
                       // 3.1 选择最多2个线特征
                        if (largestPickedNum <= 2) {
                            cloudLabel[ind] = 2;
                            cornerPointsSharp->push_back(segmentedCloud->points[ind]);
                            cornerPointsLessSharp->push_back(segmentedCloud->points[ind]);
                       // 3.2 平滑一些的线特征20个，用于mapping
                        } else if (largestPickedNum <= 20) {
                            cloudLabel[ind] = 1;
                            cornerPointsLessSharp->push_back(segmentedCloud->points[ind]);
                        } else {
                        // 3.3 超过则退出
                            break;
                        }
                        // 3.4 标记相邻点，防止特征点过于集中
                        cloudNeighborPicked[ind] = 1;
                        for (int l = 1; l <= 5; l++) {
                            int columnDiff = std::abs(int(segInfo.segmentedCloudColInd[ind + l] - segInfo.segmentedCloudColInd[ind + l - 1]));
                            if (columnDiff > 10)
                                break;
                            cloudNeighborPicked[ind + l] = 1;
                        }
                        for (int l = -1; l >= -5; l--) {
                            int columnDiff = std::abs(int(segInfo.segmentedCloudColInd[ind + l] - segInfo.segmentedCloudColInd[ind + l + 1]));
                            if (columnDiff > 10)
                                break;
                            cloudNeighborPicked[ind + l] = 1;
                        }
                    }
                }

                int smallestPickedNum = 0;
                // 4. 选择面特征，为地面，segInfo.segmentedCloudGroundFlag[ind] == true
                for (int k = sp; k <= ep; k++) {
                    int ind = cloudSmoothness[k].ind;
                    if (cloudNeighborPicked[ind] == 0 &&
                        cloudCurvature[ind] < surfThreshold &&
                        segInfo.segmentedCloudGroundFlag[ind] == true) {

                        cloudLabel[ind] = -1;
                        surfPointsFlat->push_back(segmentedCloud->points[ind]);
                        // 4.1 选择最多4个面特征
                        smallestPickedNum++;
                        if (smallestPickedNum >= 4) {
                            break;
                        }
                        // 4.2 标记相邻点
                        cloudNeighborPicked[ind] = 1;
                        for (int l = 1; l <= 5; l++) {

                            int columnDiff = std::abs(int(segInfo.segmentedCloudColInd[ind + l] - segInfo.segmentedCloudColInd[ind + l - 1]));
                            if (columnDiff > 10)
                                break;

                            cloudNeighborPicked[ind + l] = 1;
                        }
                        for (int l = -1; l >= -5; l--) {

                            int columnDiff = std::abs(int(segInfo.segmentedCloudColInd[ind + l] - segInfo.segmentedCloudColInd[ind + l + 1]));
                            if (columnDiff > 10)
                                break;

                            cloudNeighborPicked[ind + l] = 1;
                        }
                    }
                }
                // 5. 选择是地面的面特征，和其它没被选择的点（除了地面的点，并且不是线特征）
                for (int k = sp; k <= ep; k++) {
                    if (cloudLabel[k] <= 0) {
                        surfPointsLessFlatScan->push_back(segmentedCloud->points[k]);
                    }
                }
            }
            // 5.1 下采样平滑一些的面特征
            surfPointsLessFlatScanDS->clear();
            downSizeFilter.setInputCloud(surfPointsLessFlatScan);
            downSizeFilter.filter(*surfPointsLessFlatScanDS);

            *surfPointsLessFlat += *surfPointsLessFlatScanDS;
        }
    }

最后总结一下，特征点的选择满足以下3个条件。

选择的边缘点或平面点的数量不能超过每个方向上的最大值，一共有6个方向，每个方向上最多2个线特征，4个面特征。
线特征和面特征周围相邻的点不能被选中。
不能是平行于激光雷达光束的点或者被遮挡的点。

然后接着总结下代码中的输出

cornerPointsSharp 线特征（不为地面），每个方向上最多2个
cornerPointsLessSharp 比cornerPointsSharp平滑的线特征（不为地面），每个方向上20个
surfPointsFlat 面特征（为地面），每个方向上最多4个
surfPointsLessFlat 面特征（地面或者分割点云中不为线特征的点）

至此，特征提取就介绍完毕了，接着介绍特征匹配。

特征匹配

特征匹配主要是根据上述提取出的面特征和线特征进行匹配，然后根据最小二乘法，得出前后2帧的坐标转换。LeGO-LOAM相对LOAM的不同之处在于，LeGO-LOAM分别对线和面进行匹配，根据线特征匹配得到 $t_x,t_y,\theta_{yaw}$ ，根据面特征匹配得到 $t_z,\theta_{roll},\theta_{pitch}$ 。而LOAM是合并了2个匹配，一次得出 $t_x,t_y,t_z,\theta_{yaw},\theta_{roll},\theta_{pitch}$ 。

为什么LeGO-LOAM这么做呢，我们先看面特征匹配。

由于LeGO-LOAM做了地面分割，而且面特征是地面上的点，因此2个地面的点进行匹配之后，我们实际上只能保证 $t_z,\theta_{roll},\theta_{pitch}$ 是准确的。因为2个平面重叠时候 $t_z,\theta_{roll},\theta_{pitch}$ 必定是确定的。
在这里插入图片描述

如下图所示，虽然2个平面重叠了，它还可以在水平面上移动和旋转（yaw），也就是说 $t_x,t_y\theta_{yaw}$ 还可以变换，这是建立在只有水平地面的情况下，如果有多个平面，那么 $t_x,t_y\theta_{yaw}$ 也可以是确定的。
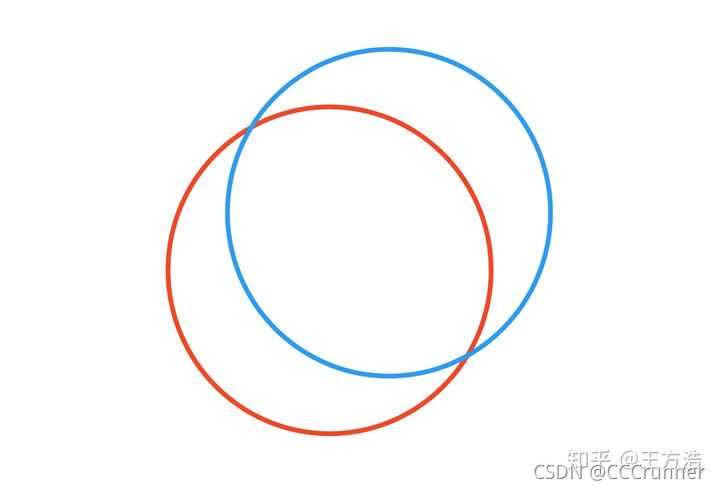
在这里插入图片描述

在通过面特征确定好 $t_z,\theta_{roll},\theta_{pitch}$ 之后，接着再根据线特征确认 $t_x,t_y,\theta_{yaw}$ 。线特征的匹配也是通过计算点到线的距离最短，通过线特征主要是确定 $t_x,t_y,\theta_{yaw}$ 。至此整个匹配的过程就完成了。通过上述方法LeGO-LOAM达到同样的精度，比LOAM节省了35%的时间。

下面我们详细介绍下特征匹配的过程，首先是线特征匹配。

线特征匹配

空间中一个点的坐标可以通过旋转和平移来转换到另一个坐标。
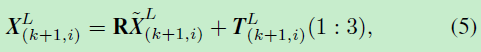
在这里插入图片描述

那么前1帧中的点通过公式(5)可以转换到当前帧，假设我们以空间中点的欧式距离来表示匹配的好坏，那么我们可以把问题转换为以下公式。
在这里插入图片描述

找到 $T_{(k+1,i)}^L$ (可以理解为公式5中的R和T)使得前一帧中所有的点通过 $T_{(k+1,i)}^L$ 转换后，和当前帧的点的欧式距离最小，这样的R和T就是前一帧和当前帧的最优坐标转换。

最小二乘法

上述的问题是不是有点类似以下经典的最小二乘法的问题。
在这里插入图片描述

我们希望找到一条直线 $Y = a X + b$ ，并且使得它和这4个点最匹配。回到坐标转换的例子，X代表前一帧的点，Y代表当前帧的点，而a代表旋转矩阵R，b代表平移矩阵b。通过计算每个点的平方差最小，来求解a和b的最优值。

代价函数

实际上LeGO-LOAM中线特征匹配不是计算2个点之间的平方差最小，而是先根据当前点i，查找它在前一帧的最小近邻点j，并且找到离j最近的l，j和l不是同一个扫描线但都属于前一帧的点云。然后再求点i到线 $(j, l)$ 的距离，实际上就是求点到线的距离。然后遍历当前帧所有的线特征，重复执行上述过程直到收敛。
在这里插入图片描述

可以看到上述最小二乘法中的代价函数没有采用点和点的匹配，而是采用线和线的匹配，而求解线和线的距离用到的是点到线的距离。也就说最小二乘法的代价函数可以定义任意的类型，而不仅仅限定于欧氏距离，你定义了什么样的代价函数，就会得到什么样的拟合结果。
在这里插入图片描述
点和线的距离

面特征匹配

面特征的匹配也是类似线特征匹配，不过是计算点到面的距离，因此根据当前帧的点i，查找上一帧中最小近邻点j，然后在当前扫描线中找到l，在相邻的扫描线中找到m，构成一个平面，然后计算点i到平面 $(j, l, m)$ 的距离。
在这里插入图片描述

点到面的距离计算公式。
在这里插入图片描述

面特征的匹配就是找到一个转换 $T_{(k+1,i)}^L$ ，使得当前帧所有点到前一帧面的距离平方差最小。
在这里插入图片描述

下面我们开始分析特征匹配的代码。

void updateTransformation(){

    if (laserCloudCornerLastNum < 10 || laserCloudSurfLastNum < 100)
        return;
    // 1. 面特征匹配
    for (int iterCount1 = 0; iterCount1 < 25; iterCount1++) {
        laserCloudOri->clear();
        coeffSel->clear();
        // 1.1 查找匹配的特征
        findCorrespondingSurfFeatures(iterCount1);

        if (laserCloudOri->points.size() < 10)
            continue;
        // 1.2 计算Transformation
        if (calculateTransformationSurf(iterCount1) == false)
            break;
    }
    // 2. 线特征匹配
    for (int iterCount2 = 0; iterCount2 < 25; iterCount2++) {

        laserCloudOri->clear();
        coeffSel->clear();
        // 2.1 查找匹配的特征
        findCorrespondingCornerFeatures(iterCount2);

        if (laserCloudOri->points.size() < 10)
            continue;
        // 2.2 计算Transformation
        if (calculateTransformationCorner(iterCount2) == false)
            break;
    }
}

calculateTransformationSurf

查找面特征和计算回归系数，点离线越远回归系数越低，离线越近的点系数越高。

void findCorrespondingSurfFeatures(int iterCount){

    int surfPointsFlatNum = surfPointsFlat->points.size();

    for (int i = 0; i < surfPointsFlatNum; i++) {
        // 1. 转换到起始点
        TransformToStart(&surfPointsFlat->points[i], &pointSel);

        if (iterCount % 5 == 0) {
            // 2.1 通过i查找j
            kdtreeSurfLast->nearestKSearch(pointSel, 1, pointSearchInd, pointSearchSqDis);
            int closestPointInd = -1, minPointInd2 = -1, minPointInd3 = -1;

            if (pointSearchSqDis[0] < nearestFeatureSearchSqDist) {
                closestPointInd = pointSearchInd[0];
                int closestPointScan = int(laserCloudSurfLast->points[closestPointInd].intensity);

                float pointSqDis, minPointSqDis2 = nearestFeatureSearchSqDist, minPointSqDis3 = nearestFeatureSearchSqDist;
                for (int j = closestPointInd + 1; j < surfPointsFlatNum; j++) {
                    if (int(laserCloudSurfLast->points[j].intensity) > closestPointScan + 2.5) {
                        break;
                    }

                    pointSqDis = (laserCloudSurfLast->points[j].x - pointSel.x) * 
                                 (laserCloudSurfLast->points[j].x - pointSel.x) + 
                                 (laserCloudSurfLast->points[j].y - pointSel.y) * 
                                 (laserCloudSurfLast->points[j].y - pointSel.y) + 
                                 (laserCloudSurfLast->points[j].z - pointSel.z) * 
                                 (laserCloudSurfLast->points[j].z - pointSel.z);

                    if (int(laserCloudSurfLast->points[j].intensity) <= closestPointScan) {
                        if (pointSqDis < minPointSqDis2) {
                          minPointSqDis2 = pointSqDis;
                          minPointInd2 = j;
                        }
                    } else {
                        if (pointSqDis < minPointSqDis3) {
                            minPointSqDis3 = pointSqDis;
                            minPointInd3 = j;
                        }
                    }
                }
                for (int j = closestPointInd - 1; j >= 0; j--) {
                    if (int(laserCloudSurfLast->points[j].intensity) < closestPointScan - 2.5) {
                        break;
                    }

                    pointSqDis = (laserCloudSurfLast->points[j].x - pointSel.x) * 
                                 (laserCloudSurfLast->points[j].x - pointSel.x) + 
                                 (laserCloudSurfLast->points[j].y - pointSel.y) * 
                                 (laserCloudSurfLast->points[j].y - pointSel.y) + 
                                 (laserCloudSurfLast->points[j].z - pointSel.z) * 
                                 (laserCloudSurfLast->points[j].z - pointSel.z);

                    if (int(laserCloudSurfLast->points[j].intensity) >= closestPointScan) {
                        if (pointSqDis < minPointSqDis2) {
                            minPointSqDis2 = pointSqDis;
                            minPointInd2 = j;
                        }
                    } else {
                        if (pointSqDis < minPointSqDis3) {
                            minPointSqDis3 = pointSqDis;
                            minPointInd3 = j;
                        }
                    }
                }
            }
            // 2.2 查找l和m
            pointSearchSurfInd1[i] = closestPointInd;
            pointSearchSurfInd2[i] = minPointInd2;
            pointSearchSurfInd3[i] = minPointInd3;
        }

        if (pointSearchSurfInd2[i] >= 0 && pointSearchSurfInd3[i] >= 0) {

            tripod1 = laserCloudSurfLast->points[pointSearchSurfInd1[i]];
            tripod2 = laserCloudSurfLast->points[pointSearchSurfInd2[i]];
            tripod3 = laserCloudSurfLast->points[pointSearchSurfInd3[i]];

            float pa = (tripod2.y - tripod1.y) * (tripod3.z - tripod1.z) 
                     - (tripod3.y - tripod1.y) * (tripod2.z - tripod1.z);
            float pb = (tripod2.z - tripod1.z) * (tripod3.x - tripod1.x) 
                     - (tripod3.z - tripod1.z) * (tripod2.x - tripod1.x);
            float pc = (tripod2.x - tripod1.x) * (tripod3.y - tripod1.y) 
                     - (tripod3.x - tripod1.x) * (tripod2.y - tripod1.y);
            float pd = -(pa * tripod1.x + pb * tripod1.y + pc * tripod1.z);

            float ps = sqrt(pa * pa + pb * pb + pc * pc);

            pa /= ps;
            pb /= ps;
            pc /= ps;
            pd /= ps;

            float pd2 = pa * pointSel.x + pb * pointSel.y + pc * pointSel.z + pd;

            float s = 1;
            if (iterCount >= 5) {
                s = 1 - 1.8 * fabs(pd2) / sqrt(sqrt(pointSel.x * pointSel.x
                        + pointSel.y * pointSel.y + pointSel.z * pointSel.z));
            }
            // 3. 计算回归系数
            if (s > 0.1 && pd2 != 0) {
                coeff.x = s * pa;
                coeff.y = s * pb;
                coeff.z = s * pc;
                coeff.intensity = s * pd2;

                laserCloudOri->push_back(surfPointsFlat->points[i]);
                coeffSel->push_back(coeff);
            }
        }
    }
}

最小二乘法求解

通过回归系数求解坐标转换Transformation[4]

bool calculateTransformationSurf(int iterCount){

        int pointSelNum = laserCloudOri->points.size();

        cv::Mat matA(pointSelNum, 3, CV_32F, cv::Scalar::all(0));
        cv::Mat matAt(3, pointSelNum, CV_32F, cv::Scalar::all(0));
        cv::Mat matAtA(3, 3, CV_32F, cv::Scalar::all(0));
        cv::Mat matB(pointSelNum, 1, CV_32F, cv::Scalar::all(0));
        cv::Mat matAtB(3, 1, CV_32F, cv::Scalar::all(0));
        cv::Mat matX(3, 1, CV_32F, cv::Scalar::all(0));

        float srx = sin(transformCur[0]);
        float crx = cos(transformCur[0]);
        float sry = sin(transformCur[1]);
        float cry = cos(transformCur[1]);
        float srz = sin(transformCur[2]);
        float crz = cos(transformCur[2]);
        float tx = transformCur[3];
        float ty = transformCur[4];
        float tz = transformCur[5];

        float a1 = crx*sry*srz; float a2 = crx*crz*sry; float a3 = srx*sry; float a4 = tx*a1 - ty*a2 - tz*a3;
        float a5 = srx*srz; float a6 = crz*srx; float a7 = ty*a6 - tz*crx - tx*a5;
        float a8 = crx*cry*srz; float a9 = crx*cry*crz; float a10 = cry*srx; float a11 = tz*a10 + ty*a9 - tx*a8;

        float b1 = -crz*sry - cry*srx*srz; float b2 = cry*crz*srx - sry*srz;
        float b5 = cry*crz - srx*sry*srz; float b6 = cry*srz + crz*srx*sry;

        float c1 = -b6; float c2 = b5; float c3 = tx*b6 - ty*b5; float c4 = -crx*crz; float c5 = crx*srz; float c6 = ty*c5 + tx*-c4;
        float c7 = b2; float c8 = -b1; float c9 = tx*-b2 - ty*-b1;

        for (int i = 0; i < pointSelNum; i++) {

            pointOri = laserCloudOri->points[i];
            coeff = coeffSel->points[i];

            float arx = (-a1*pointOri.x + a2*pointOri.y + a3*pointOri.z + a4) * coeff.x
                      + (a5*pointOri.x - a6*pointOri.y + crx*pointOri.z + a7) * coeff.y
                      + (a8*pointOri.x - a9*pointOri.y - a10*pointOri.z + a11) * coeff.z;

            float arz = (c1*pointOri.x + c2*pointOri.y + c3) * coeff.x
                      + (c4*pointOri.x - c5*pointOri.y + c6) * coeff.y
                      + (c7*pointOri.x + c8*pointOri.y + c9) * coeff.z;

            float aty = -b6 * coeff.x + c4 * coeff.y + b2 * coeff.z;

            float d2 = coeff.intensity;

            matA.at<float>(i, 0) = arx;
            matA.at<float>(i, 1) = arz;
            matA.at<float>(i, 2) = aty;
            matB.at<float>(i, 0) = -0.05 * d2;
        }

        cv::transpose(matA, matAt);
        matAtA = matAt * matA;
        matAtB = matAt * matB;
        // 1. 最小二乘法求解
        cv::solve(matAtA, matAtB, matX, cv::DECOMP_QR);

        if (iterCount == 0) {
            cv::Mat matE(1, 3, CV_32F, cv::Scalar::all(0));
            cv::Mat matV(3, 3, CV_32F, cv::Scalar::all(0));
            cv::Mat matV2(3, 3, CV_32F, cv::Scalar::all(0));

            cv::eigen(matAtA, matE, matV);
            matV.copyTo(matV2);

            isDegenerate = false;
            float eignThre[3] = {10, 10, 10};
            for (int i = 2; i >= 0; i--) {
                if (matE.at<float>(0, i) < eignThre[i]) {
                    for (int j = 0; j < 3; j++) {
                        matV2.at<float>(i, j) = 0;
                    }
                    isDegenerate = true;
                } else {
                    break;
                }
            }
            matP = matV.inv() * matV2;
        }

        if (isDegenerate) {
            cv::Mat matX2(3, 1, CV_32F, cv::Scalar::all(0));
            matX.copyTo(matX2);
            matX = matP * matX2;
        }

        transformCur[0] += matX.at<float>(0, 0);
        transformCur[2] += matX.at<float>(1, 0);
        transformCur[4] += matX.at<float>(2, 0);

        float deltaR = sqrt(
                            pow(rad2deg(matX.at<float>(0, 0)), 2) +
                            pow(rad2deg(matX.at<float>(1, 0)), 2));
        float deltaT = sqrt(
                            pow(matX.at<float>(2, 0) * 100, 2));
        // 2. 结果收敛则返回
        if (deltaR < 0.1 && deltaT < 0.1) {
            return false;
        }
        return true;
    }