目录
引言:
TSP问题:
概念:
TSP问题,全称为旅行商问题(Traveling Salesman Problem),可以描述为:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
特性:
组合性:随着城市数量的增加,可能的行程数量将呈阶乘级增加(如10个城市,可能的路线总共有10!种),导致问题的求解空间巨大。
NP难性:没有多项式时间复杂度的已知算法可以解决TSP问题,即无法确保在合理时间内找到最优解。
应用领域(包括但不限于以下领域):
1、道路交通规划:如何规划最合理高效的道路交通,以减少拥堵。
2、电路板线路设计:在设计电路板时,如何找到最优的线路布局。
3、物流配送:如何更好地规划物流,以减少运营成本。
遗传算法:
简介:
遗传算法(Genetic Algorithm, GA)是一种模拟自然选择和遗传学原理的优化搜索算法。它借鉴了达尔文的进化论和孟德尔的遗传学说,通过模拟自然进化过程搜索最优解。遗传算法广泛应用于函数优化、机器学习、组合优化、自适应控制等领域。
算法原理:
1、编码:首先需要将现实问题的解空间映射到遗传算法的搜索空间,说人话就是需要将实际问题的解的结构写成像DNA那样的链式结构,方便遗传算法进行处理。
2、初始种群:遗传算法会进行很多次种群进化(即代码迭代),但在此之前需要生成一个初始种群(一般根据具体情况随机生成),以便进行后续的迭代操作。
3、适应度函数:用来评估个体的优劣,以便进行选择操作。通常根据问题的目标函数来设计适应度函数(如本文中需要评估某条路线的总距离,并且越短越好,那么适应度值就可以设置为总距离的倒数),适应度越大,说明该个体越优秀。
4、选择:根据个体的适应度值,按照一定的规则或方法(一般为轮盘赌)从当前种群中选择出优良的个体,使它们有机会作为父代进行部分信息的交叉,为后续产生两个新子体做准备。选择操作体现了达尔文的适者生存原则。
5、信息交叉(杂交配对):将选择操作得到的两个父代个体的部分结构加以替换重组而生成新个体的操作。交叉操作体现了信息交换的思想。
6、变异:模拟生物在自然的遗传环境中由于各种偶然因素引起的基因变异,并以很小的概率随机地改变遗传基因(表示解的数据链的某些点位)的值。变异操作可以增加种群的多样性并有机会跳出局部最优解。
7、终止条件:当算法满足某种终止条件时,将停止运行。常见的终止条件包括达到预设的迭代次数、找到满足要求的解等。
代码流程:
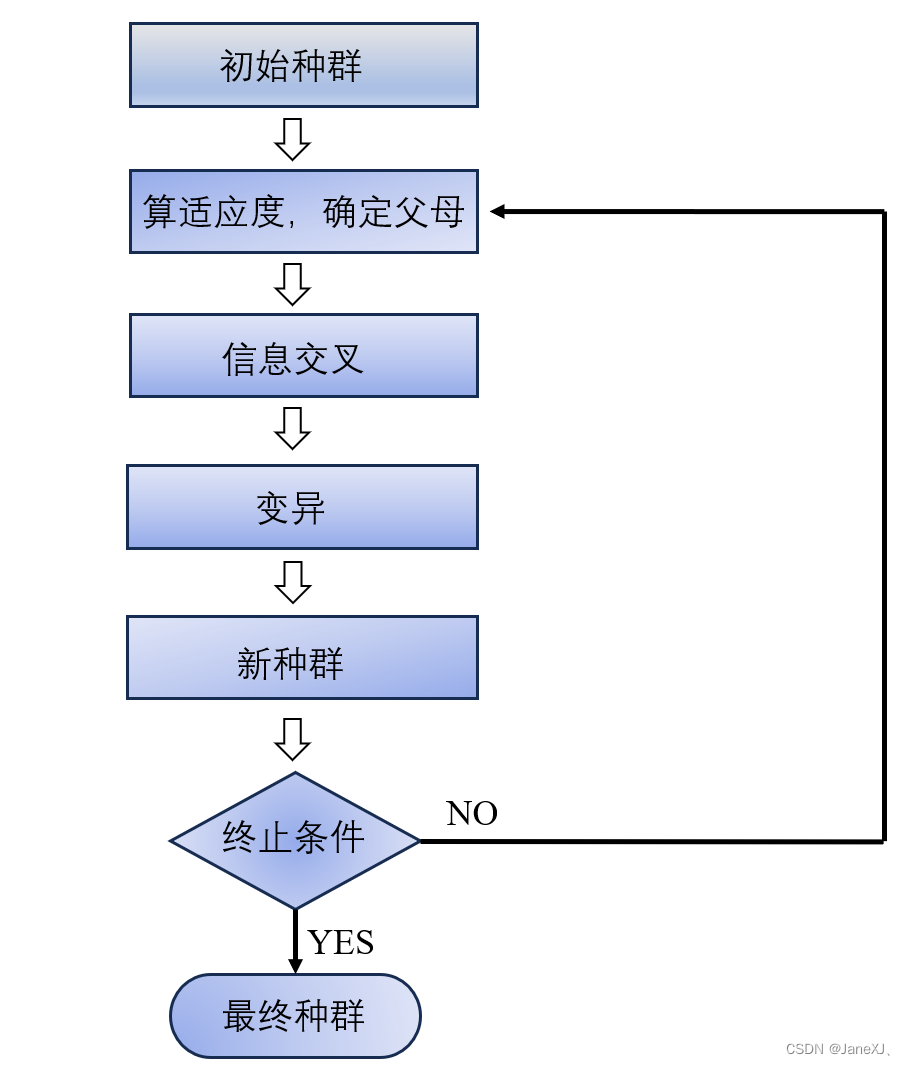
特点:
1、并行性:遗传算法采用种群的方式进行搜索,可以同时搜索解空间中的多个区域。
2、自适应性:遗传算法通过适应度函数来评估个体的优劣,不需要其他外部信息。
3、全局搜索能力:遗传算法通过交叉和变异操作可以产生新的个体,从而跳出局部最优解,具有全局搜索能力。
4、鲁棒性:遗传算法对问题的依赖性较小,可以应用于不同类型的优化问题。
5、易于实现:遗传算法的编码和操作相对简单,易于在计算机上实现。
话不多说,下面咱们直接上代码。。。
代码实现:
本文代码实现需要导入的模块如下所示。random模块用于实现随机数等操作,time模块用于记录迭代时长,其余3个模块用于进行数据可视化。
import random
import time
from matplotlib import pyplot as plt
from pyecharts.charts import Line
from pyecharts.options import *1、城市定义
定义一个嵌套列表city,内部包含各个城市的数据,每一个数据为[城市号,x坐标,y坐标],
再定义一个列表number记录每个城市的城市号,后续通过number里的城市号来从city里检索其对应城市的坐标等数据。当然,这些城市的x,y坐标可以随意定义,甚至城市数量也可以任意。本文这里定义20个城市。
# 定义一个20*3的矩阵,分别代表20个城市以及各自的x和y坐标
city: list[list[int]] = [
[1, 54, 51],
[2, 22, 67],
[3, 4, 26],
[4, 57, 62],
[5, 12, 42],
[6, 38, 32],
[7, 61, 31],
[8, 21, 14],
[9, 79, 10],
[10, 29, 15],
[11, 52, 33],
[12, 82, 27],
[13, 21, 96],
[14, 37, 91],
[15, 9, 75],
[16, 74, 76],
[17, 17, 27],
[18, 65, 94],
[19, 70, 71],
[20, 41, 98]]
number = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20] # 城市序号2、定义产生初始种群的函数
实现遗传算法的第一步是先产生一个初始种群,对于本文的TSP问题来说,初始种群是一系列的路线,每条路线都是由random.sample方法从number里随机抽取20个数产生(顺序随机)。本文产生初始种群的first_solution函数接收一个入口参数cnt,函数最后返回一个嵌套列表,内部包含cnt条路线。
def first_solution(cnt: int) -> list[list[int]]: # 产生初始种群,cnt*20的矩阵
result: list[list[int]] = []
for i in range(cnt):
result.append(random.sample(number, 20))
return result3、定义一个函数来计算某条路线的总距离
由于后续需要从种群中选出适应度高的优秀个体,对于TSP问题来说,适应度体现在总距离的大小上,因此本文封装了一个函数来求某条路线的总距离。函数的入口参数为一个列表,该列表代表一条路线,由于完整的路线应该是首尾相连形成闭环,故该函数首先加上起点城市形成新的列表,再用循环从头依次遍历列表里的城市对,计算每对城市之间的欧式距离,然后进行累加,最后返回该条路线的总距离。并且在累加距离时考虑到两个城市的x,y坐标一样时会导致距离为0的问题,该函数在dist与total_dist为0时用一个很小的数将其替代(0.1和1),这样做是为了避免在计算适应度的时候产生的除0问题。
def dist_comput(route: list[int]) -> float: # 计算某个路线的总距离
total_dist = 0 # 某个解的总距离
full_path = route + [route[0]]
for j in range(len(full_path)-1):
x1 = city[full_path[j]-1][1]
y1 = city[full_path[j]-1][2]
x2 = city[full_path[j+1]-1][1]
y2 = city[full_path[j+1]-1][2]
dist = (abs(x1-x2) ** 2 + abs(y1-y2) ** 2) ** 0.5
if dist == 0:
dist = 0.1
total_dist += dist
if total_dist == 0:
total_dist = 1
return total_dist4、定义适应度函数
由于我们希望种群中适应度越大的个体被选择为父母的几率越大,因此这里定义一个适应度函数来计算某个种群中每条路线的适应度。遗传算法的适应度应该根据具体问题具体定义,对于本文的TSP问题,适应度为总距离的倒数。函数的入口参数为一个嵌套列表,表示某个种群,返回一个列表,该列表为种群中每条路线的归一化选择概率(之所以返回归一化选择概率,是为了给后续建立轮盘赌做准备)
def fitness(solu: list[list[int]]) -> list[float]: # 计算某个解集所有解的适应度,返回归一化选择概率
fitness_list: list[float] = [] # 存储每个解的适应度,为每个解总距离的倒数
for i in range(len(solu)):
total_dist = dist_comput(solu[i])
fitness_list.append(1/total_dist)
prob_one = [item/sum(fitness_list) for item in fitness_list] # 归一化选择概率
return prob_one5、选择父母并交叉信息
前面提到我们需要用轮盘赌的方法来选择优秀的个体成为父母并进行后续的信息交叉。所谓轮盘赌就如同掷飞镖一样,当圆盘中某块区域面积越大,那么飞镖落在该区域的几率就越大。翻译成代码就是构建一条0-1的数轴(由归一化选择概率依次累加构成),其中分成许多段,代表不同的选择概率,此时随机生成一个0-1的浮点数(代表前面所说的飞镖),该数落在数轴的哪一段,就选择该段所对应的路线作为父体。该操作进行2次,就选择好了两个父体(每个父体都是一条路线),如下代码所示。
parents: list[list[int]] = [] # 存储父母
for i in range(2): # 生成随机数来进行轮盘赌,确定父母
rand = random.uniform(0, 1)
for k in range(len(one_prob)):
if k == 0:
if rand < one_prob[k]:
parents.append(solution[k])
else:
if one_prob[k-1] <= rand < one_prob[k]:
parents.append(solution[k])接着便是两个父体的信息交叉。本文的交叉策略是两个父体互相交换一段长度为5的片段,并且此片段在两个父体中的位置下标相同,就像下图展示的一样,sec0在P0中的下标为2-6,而sec1在P1中的下标也是2-6。既然他们所在下标都是一样的,那么我们就可以用一个数rand来控制两个父体所要发生交换的片段,即sec0=P0[rand:rand+5](考虑到交换的片段长度为5),sec1同理。而这里的rand可以使用随机数来生成(范围为0-14,考虑到城市号的下标范围为0-19且交换片段长度为5)。
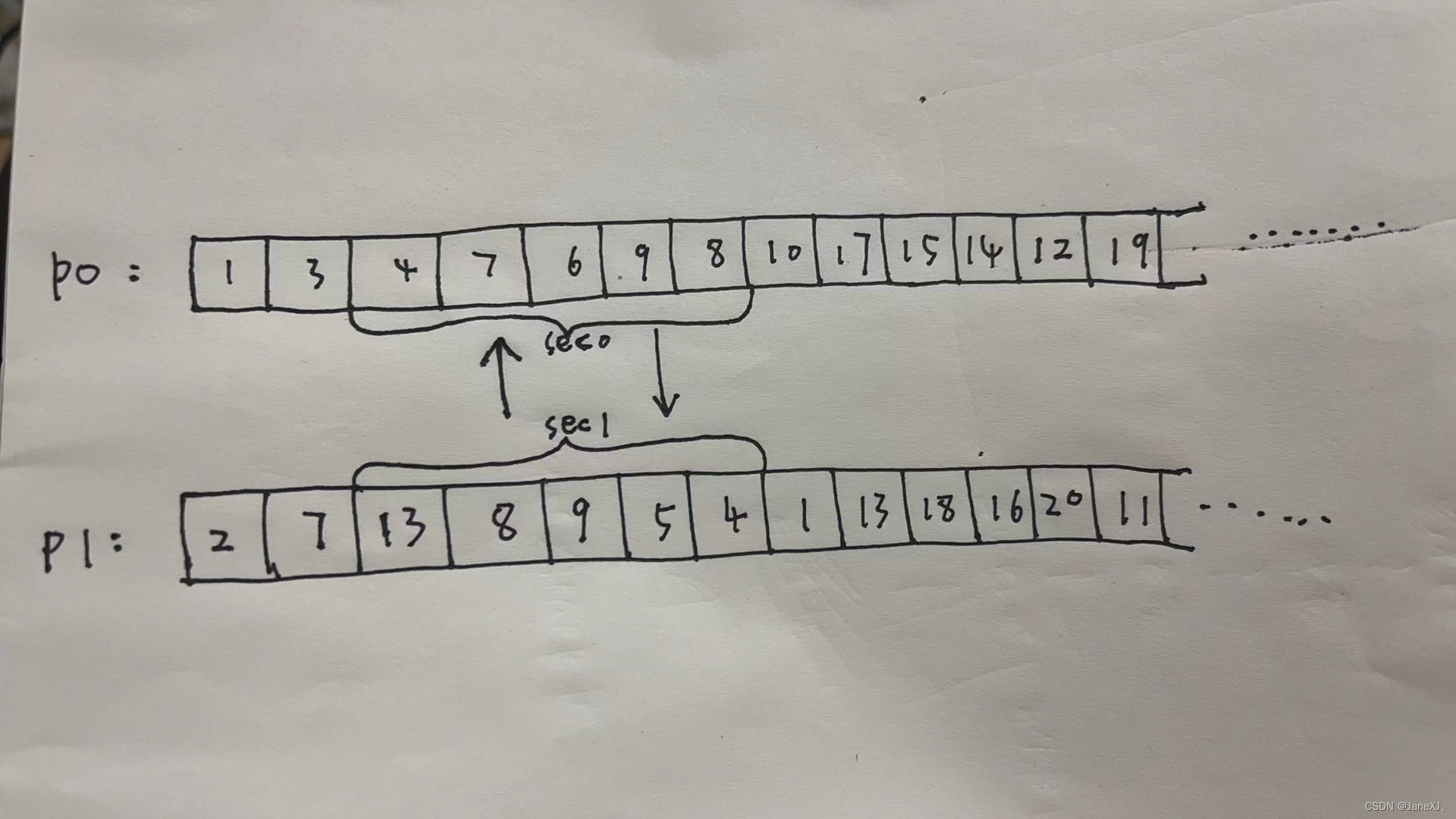
这里还有一个问题,就是如果P1从P0获得[1,2,3,4,5],而P0从P1获得[6,7,8,9,10],那么P1新获得的[1,2,3,4,5]就会与原来已经存在的[1,2,3,4,5]冲突,而P0新获得的[6,7,8,9,10]就会与原来已经存在的[6,7,8,9,10]冲突。 因为路线中城市号应该是唯一的,所以这个问题必须解决。
我们要注意一点:P0与P1都是包含20个数的列表,并且都是1-20的数且不重复。那么拿上面的交换举例子,P1获得了[1,2,3,4,5],但是失去了[6,7,8,9,10],那么对P1来说,就是失去的东西没有补回来,而获得的东西又是本来已经拥有的,P0同理。那么我们就能想到一种解决办法,就是在交换前把P1原来的[1,2,3,4,5]所对应位置的城市号依次换成[6,7,8,9,10],这样在完成交换后,P1获得了[1,2,3,4,5],而丢失的[6,7,8,9,10]也补上了,P0同理。
假设P0要发生交换的片段是sec0,而P1要发生交换的片段是sec1,那么上面的解决方法翻译成代码就是:遍历sec0中的每个城市号,取得该城市号在P1中的下标,并将该下标对应的城市号换成sec1中的城市号,P0同理。
这里还有一个细节,那就是sec0与sec1可能有重复的城市号,对于这些重复的城市号来说,进行上一段中的操作是多余的,因为假如你丢了一块钱,但是又从其他地方捡到一块钱,那么总的来说你的钱没有多也没有少。因此我们需要剔除掉sec0与sec1中存在的公共部分而分别形成new_sec0与new_sec1,此时他们不存在重复的城市号。产生new_sec0与new_sec1的函数如下所示。
def remove_common_elements(sec0: list[int], sec1: list[int]): # 去除两个列表sec0和sec1中相同的元素,并返回两个新的列表
# 转换为集合以快速查找公共元素
set0 = set(sec0)
set1 = set(sec1)
# 计算公共元素
common_elements = set0 & set1
# 去除公共元素后构建新的列表
new_sec0 = [x for x in sec0 if x not in common_elements]
new_sec1 = [x for x in sec1 if x not in common_elements]
return new_sec0, new_sec1
2个父体在完成上面的信息交换后,会产生2个新子体,但是我们总共需要产生与原先种群数量相当的新子体,以便形成新的种群,因此最外层还应该套一个大循环,循环次数为len(原种群)//2。最后就是判断新子体是否优于父体,来决定是否加入新种群。本文还在函数外定义了一个变量来记录总共交叉的次数。多的不说,咱们下面直接上代码。
def select_crossover(solution: list[list[int]]) -> list[list[int]]: # 入口参数为一个种群,选择并交叉优秀父母的信息,返回新的种群
global cross_num # 记录交叉次数
new_group: list[list[int]] = []
one_prob = fitness(solution)
for i in range(1, len(one_prob)): # 叠加选择概率,创建轮盘赌
one_prob[i] += one_prob[i-1]
for n in range(len(solution)//2):
parents: list[list[int]] = [] # 存储父母
for i in range(2): # 生成随机数来进行轮盘赌,确定父母
rand = random.uniform(0, 1)
for k in range(len(one_prob)):
if k == 0:
if rand < one_prob[k]:
parents.append(solution[k])
else:
if one_prob[k-1] <= rand < one_prob[k]:
parents.append(solution[k])
p0 = parents[0][:]
p1 = parents[1][:]
rand = random.randint(0, 14)
sec0 = p0[rand:rand+5][:]
sec1 = p1[rand:rand+5][:]
new_sec0, new_sec1 = remove_common_elements(sec0, sec1)
for i in new_sec0:
for j in range(len(p1)):
if p1[j] == i:
p1[j] = new_sec1[new_sec0.index(i)] # 去重以保证城市唯一性
son1 = p1[:rand] + sec0 + p1[rand+5:] # 子体son1
for i in new_sec1:
for j in range(len(p0)):
if p0[j] == i:
p0[j] = new_sec0[new_sec1.index(i)] # 去重以保证城市唯一性
son0 = p0[:rand] + sec1 + p0[rand+5:] # 子体son0
# 检查产生的子代是否比父代优秀,是则加入新种群,否则不加入
if dist_comput(son0) < dist_comput(p0):
new_group.append(son0)
cross_num += 1
else:
new_group.append(parents[0][:])
if dist_comput(son1) < dist_comput(p1):
new_group.append(son1)
cross_num += 1
else:
new_group.append(parents[1][:])
return new_group6、变异
变异可以提高种群的多样性并跳出局部最优解。那么对于本文的TSP问题来说,变异操作就是将原先某条路线的某个或多个点位的城市号替换成另外的城市号,但这样会带来一个问题:城市号重复,即假如原先路线中的城市号5变异成6,那么这个新的城市号6就会与原先已经存在的城市号6冲突。本文的解决方法是:生成一个随机数k来代表将要发生变异的城市下标,然后将原来路线中下标为k与k+1的两个城市号交换顺序。由于原来路线中的城市号都是不重复的,因此这样交换顺序的操作一定可以产生新的路线并且每个点位都有机会发生变异,最重要的是,这样可以避免前面所说的城市号重复的问题,只是需要注意k的范围是[0,len(old_route)-2]。变异函数如下所示,通过手动输入变异率,并生成一个0-1的随机浮点数来决定是否发生变异。若变异,则进行交换操作;若不变异,则原封不动。当然也要保证变异后的个体优于变异前。当然本文也在变异函数外定义了一个变量来记录总共的变异次数。函数最后返回一个新的种群。如下所示。
def mutation(group: list[list[int]], rate: float) -> list[list[int]]: # 生成随机数进行随机某个点位的变异,返回变异后的新种群
global mut_num # 跟踪变异次数
new_group: list[list[int]] = []
for i in range(len(group)):
rand = random.uniform(0, 1)
copy_1 = group[i][:]
if rand < rate: # 生成的随机数小于变异概率,则进行变异操作
k = random.randint(0, len(copy_1)-2)
copy_1[k], copy_1[k+1] = copy_1[k+1], copy_1[k] # 变异规则为:使路线中下标为k与k+1的城市交换
if dist_comput(copy_1) < dist_comput(group[i]): # 确保变异后的子代优于父代
new_group.append(copy_1)
mut_num += 1
else:
new_group.append(group[i][:])
else:
new_group.append(group[i][:])
return new_group7、主逻辑
有了前面的准备,我们就可以使用一个大循环来模拟遗传算法的迭代过程了。
主逻辑将完全遵循前面引言中提到的遗传算法的代码流程,即1、产生初始种群,2、算当前种群的适应度并选择父母进行信息交叉,3、变异,4、判断是否满足终止条件,若满足则结束循环,若不满足则一直执行第2、3、4步。本文的终止条件为预设的迭代次数。主逻辑部分的代码如下所示。
start_time = time.time()
cross_num = 0 # 总共的交叉次数
mut_num = 0 # 总共的变异次数
popu_scale = 500 # 种群规模
gen_num = 500 # 迭代次数
temp_solu = first_solution(popu_scale) # 中间解,这是第一代,即初始种群
first_dist = dist_comput(temp_solu[0])
print(f"初始路线为:")
print_route(temp_solu[0])
print(f"总距离:{first_dist}")
good_son = [] # 存储每一代种群中最优秀的个体,总共有gen_num个数据
for i in range(gen_num):
temp_solu = select_crossover(temp_solu)
temp_solu = mutation(temp_solu, 0.05)
# 到这一步,新一代种群已经产生
distance = [] # 新种群所有路线的距离
for i in range(len(temp_solu)):
distance.append(dist_comput(temp_solu[i]))
best_idx = distance.index(min(distance)) # 新种群中最优个体索引
good_son.append([temp_solu[best_idx], min(distance)])
good_son_copy = good_son[:] # 用于后续可视化
good_son.sort(key=lambda f: f[1], reverse=False) # 按距离升序排列
print(f"进化{gen_num}代,交叉{cross_num}次,变异{mut_num}次后,给出的近似最优路线为:")
print_route(good_son[0][0])
print(f"总距离:{good_son[0][1]}")
end_time = time.time()
print(f"迭代所用时长:{end_time-start_time}秒")
# 查找最优个体在第几代
smallest_num = float("inf")
smallest_num_idx = None
for idx, item in enumerate(good_son_copy):
if item[1] < smallest_num:
smallest_num = item[1]
smallest_num_idx = idx
print(f"最优个体出现在第{smallest_num_idx+2}代")其中种群规模设置成500,代表每个种群中有500条路线。
迭代次数为500。
首先利用first_solution函数生成初始种群temp_solu,并打印出完整的初始路线temp_solu[0]及其总距离。这里所说的路线的“完整”即需要打印出从某城市出发最后又回到该城市的闭环路线,因此这里封装了一个print_route函数用来打印完整路线。函数代码很简单,如下所示。
def print_route(road: list[int]): # 用于打印完整路线
for i in range(len(road)):
print(f"{road[i]} -> ", end="")
print(f"{road[0]}")之后定义了一个good_son列表用来存储每一代种群中最优秀的个体。
接着便是种群的进化迭代(for循环),首先让初始种群进行选择交叉操作,再进行变异,然后赋值给temp_solu。此时的temp_solu已经是新的种群,为了筛选出新种群中最优秀的个体,我们需要一个指标来对新种群中的个体优劣进行评估,相信有小伙伴已经猜到是什么指标了,没错!就是距离,因此我们这里计算新种群中所有路线的距离并找出距离最短的路线,该路线即为新种群中最优秀的个体。
之后再将新种群中的最优路线及其对应的距离构成一个列表加入到good_son中。之所以要额外添加距离到good_son中,是因为后续我们需要找到这500代中最优秀的个体(即优秀个体中最优秀的那个),这就需要一个指标将每一代的最优个体进行一个排序。当然,也是为了方便后续的数据可视化。
最后便是通过排序找出进化500代后的最终极优秀的那个个体(即本文TSP问题中的近似最优解),并打印其完整路线以及总距离。最后还给出迭代所用时长以及首个最优个体出现在哪一代。
最终运行效果如下所示(由于遗传算法本身的随机性及其各种参数设置的不同,使得可能每次给出的最优解都不相同(局部最优解)而无法找到全局最优解,因此只能向最优解逼近,而且也不是迭代次数越多解越优秀,如本次执行中迭代500次,但是首个最优个体出现在第103代)。当然,通过选择合理的选择、交叉以及变异策略,以及合理的参数设置,我们有机会取得全局最优解,本文这里不做深入探讨。

8、数据可视化
若我们需要直观的结果呈现或者要解决实际生产中的路径规划问题,那么我就需要绘制出最优路线图。绘图的逻辑很简单,首先是定义2个列表分别存储所有x坐标和所有y坐标,然后定义name列表用来存储20个城市的城市号。接着便是绘制点并为每个点命名,然后用箭头线段依次连接并首尾相连,最后用红色突出起点并设置x,y坐标轴标签和图像标题。结果如下所示。
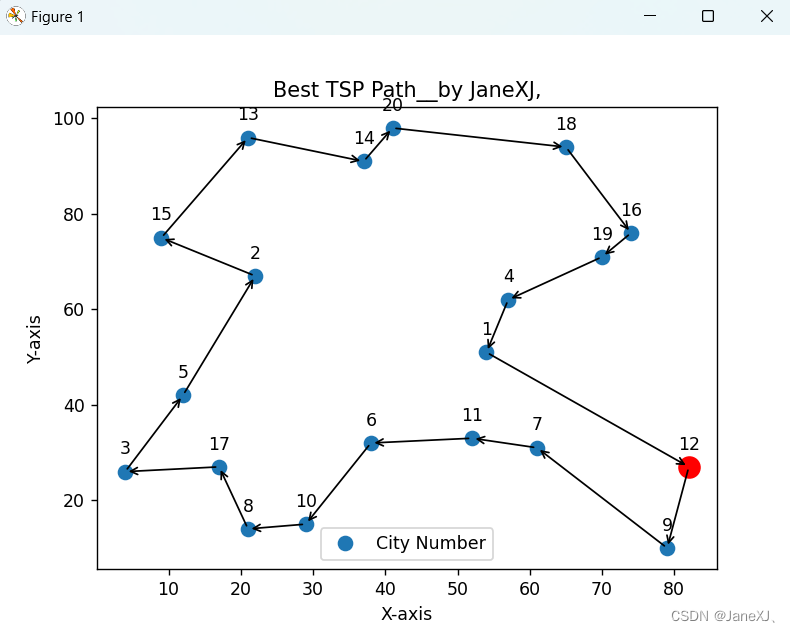
也许我们想要观察迭代的整体情况,本文也绘制了一个折线图来简单表示迭代过程。绘制的逻辑很简单,这里不作解释。以下为执行结果。
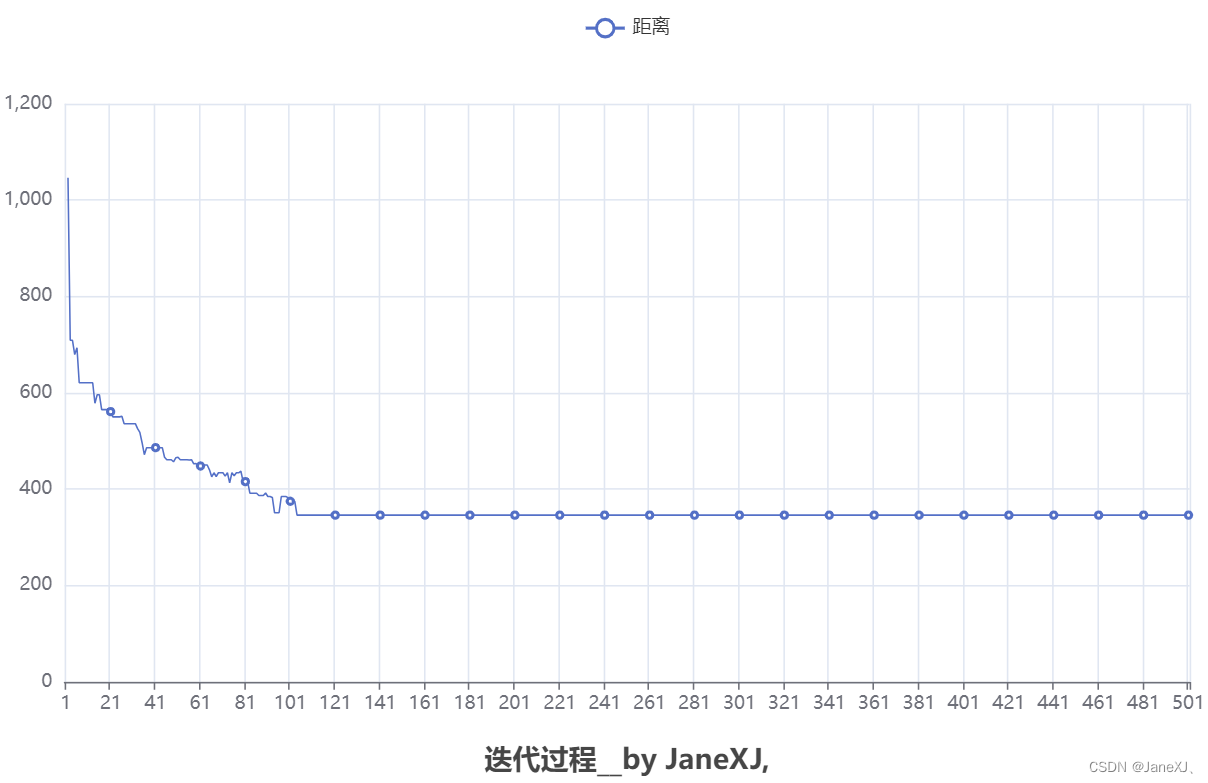
与代码执行的结果一样,从图中可以看出,当迭代到了第103代,已经达到了最优效果(局部),之后的迭代效果几乎无变化,即曲线已经收敛。
总结:
本文中的代码还有很多地方可以改进以获得全局最优解。比如:1、精进选择父母的策略 2、改进交叉的方式(如部分匹配交叉、顺序交叉、循环交叉,具体请读者自行查阅文献)3、改变变异的策略 4、种群参数的设置,如种群规模,迭代次数、变异率等等 5、初始种群的产生方式 6、。。。。。。
遗传算法作为一种启发式的优先搜索算法,本身受内部许多参数影响,特别是其基于概率的搜索机制,它在搜索过程中可能会陷入局部最优解而无法找到全局最优解。并且遗传算法需要进行大量的迭代和随机操作,导致计算复杂度较高。而且对于许多问题,无法准确找到一个合适的适应度函数来评估种群中个体的优劣,这会增加在实际工作中的难度。在实际使用时,建议将遗传算法与其他优化算法相结合,如模拟退火算法(Simulated Annealing)或粒子群优化算法(Particle Swarm Optimization)等,结合各自的优势来提高搜索效果。
最后,若有小伙伴有疑问或者有改进的意见等,欢迎在评论区与我进行讨论,求赞求赞^v^























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








