1. TSP问题
旅行商问题(Travelling salesman problem, TSP)是运筹学和理论计算机科学中经典的问题.具体问题如下:给定一系列城市和每对城市之间的距离,求解访问每座城市一次并回到起始城市的最短回路.

2. 动态规划
本节参考旅行商问题(动态规划)
2.1 理论介绍
假设节点数较少的TSP问题,我们完全可以使用穷举的方式得到最优解,但是在穷举过程中一定存在很多重复的计算.这时候我们就可以使用动态规划来避免这些重复计算以提高效率.
熟悉动态规划的同学一定知道,凡是可以使用动态规划求解优化问题,说明问题本身一定含有最优子问题,换言之,求解得到最优解,一定是由子问题的最优解组成.
换成数学的语言表达即,假设当前问题是想知道从节点i出发,访问剩余节点集合V的最短路径,将该问题表达成
d ( i , V ) d(i, V) d(i,V)
假如下一个节点选择了k节点能使该问题有最优解,那么本问题必定包含了子问题
d
(
k
,
V
−
{
k
}
)
d(k, V-\{\mathrm k\})
d(k,V−{k}),即从节点k出发访问剩余节点集合
V
−
{
k
}
V-\{\mathrm k\}
V−{k}.这是显而易见的,不妨反过来想,如果子问题不是最优,那么本问题一定不是最优的.
经过上面的分析,不难得出下面的动态规划方程:
d ( i , V ) = { c i s , V = ∅ , i ≠ s min { c i k + d ( k , V − { k } ) } , k ∈ V , i ∉ V , V ≠ ∅ \mathrm d(\mathrm i,\mathrm V)=\begin{cases}c_{is},&\quad\mathrm V=\emptyset,\mathrm i\neq\mathrm s\\\min\{c_{ik}+\mathrm d(\mathrm k,\mathrm V-\{\mathrm k\})\},&\quad\mathrm k\in\mathrm V, \mathrm i \notin \mathrm V,\mathrm V\neq\emptyset\end{cases} d(i,V)={cis,min{cik+d(k,V−{k})},V=∅,i=sk∈V,i∈/V,V=∅
2.2 算法实现
有了上面的理论分析,基于动态规划求解TSP的算法实现就很容易理解.
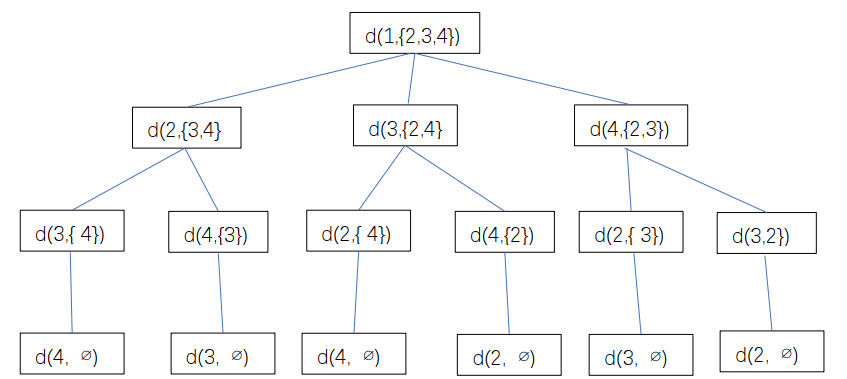
利用动态规划方程我们很容易自底向上的计算各个子问题,直至得到我们想要求解的问题.具体操作就是使用一个DP表(下表是从节点0出发得到的DP表).
| 索引 | {null} | {1} | {2} | {1,2} | {3} | {1, 3} | {2, 3} | {1,2,3} |
|---|---|---|---|---|---|---|---|---|
| 0 | / | / | / | / | / | / | / | d(0, {1,2,3}) |
| 1 | c(0,1) | / | d(1,{2}) | / | d{1,{3}} | / | d(1,{2,3}) | / |
| 2 | c(0,2) | d(2,{1}) | / | / | d(2,{3}) | d(2,{1,3}) | / | / |
| 3 | c(0,3) | d(3,{1}) | d(3,{2}) | d(3,{1,2}) | / | / | / | / |
该表的更新顺序可以从左侧列开始递推到右侧列.注意DP表的维度,假设有n个节点(包含1个起始节点):
- 有n行
- 有 2 n − 1 2^{n-1} 2n−1列
递推过程还需要遍历n次比较求 min { c i k + d ( k , V − { k } ) } \min\{c_{ik}+\mathrm d(\mathrm k,\mathrm V-\{\mathrm k\})\} min{cik+d(k,V−{k})}.因此通过动态规划求解TSP问题的时间复杂度为 O ( 2 n n 2 ) O(2^n n^2) O(2nn2),因此大规模的TSP问题不能直接使用动态规划的方法求解.
def SolveTspByDp(nodes, close = False):
"""
@brief: 动态规划解决 旅行商
@note: 只适合小规模的运算 20个节点内
@param nodes: 节点数组,nodes[0]是起点
@param close: true-寻找最优的闭环路径(回到起点)
false-非闭环最优路径
"""
n = len(nodes)
m = 1 << (n - 1)
distances = np.zeros((n, n))
for i in range(n):
for j in range(n):
if i != j:
distances[i][j] = (nodes[i] - nodes[j]).Norm()
# dx = nodes[i][0] - nodes[j][0]
# dy = nodes[i][1] - nodes[j][1]
# distances[i][j] = math.sqrt(dx*dx + dy*dy)
dp = []
for i in range(n):
dp.append([1e10] * m)
# 初始化DP表
if close:
# 考虑回到起点的情况
for i in range(n):
dp[i][0] = distances[i][0]
else:
# 不考虑回到起点的情况
for i in range(n):
dp[i][0] = 0
for j in range(1, m):
for i in range(1, n):
dp[i][j] = 1e10
if j >> (i-1) & 1:
continue
for k in range(1, n):
if not (1 << (k-1) & j):
continue
tmp = distances[i][k] + dp[k][j ^ (1 << (k-1))]
if tmp < dp[i][j]:
dp[i][j] = tmp
# 初始化路径并插入起点
path = [0]
s = m - 1
while True:
minValue = 1e10
index = 0
for i in range(1, n):
if not ((1 << (i-1)) & s):
continue
tmp = distances[path[-1]][i] + dp[i][s ^ (1 << (i-1))]
if tmp < minValue:
minValue = tmp
index = i
path.append(index)
s = s ^ (1 << (index-1))
if not s:
break
return path
3. 蚁群算法
本节参考
上面提到,当TSP问题的规模较大时,基于动态规划的方法效率太低,不适合求解.这时候可能难以求解全局最优解,而只能采用概率方式求解近似最优解.
蚁群算法(Ant Colony Optimization, ACO)是一种在图中寻找优化路径的几率性算法,其核心思想来源于蚂蚁寻找食物过程中发现路径的行为,是一种模拟进化算法.
蚁群求解TSP问题其实很直观,每一次迭代过程中会先随机投放m只蚂蚁,每只蚂蚁在每个节点时面临一个问题,即如何选择下一个节点?
3.1 节点的选择
节点的选择取决于两部分因素:
- 当前节点与其它节点的距离:该值是作为一个启发值引导蚂蚁优先选择到下一个节点代价更低的;
- 信息素:信息素的名字就是直接来源于生物学上的叫法,其作用是根据历史迭代中总结的"经验",历史路径的距离越小则信息素浓度越高.
往下一个节点移动的概率用公式表达如下:
p i j k ( t ) = { [ τ i j ( t ) ] α [ η i j ] β ∑ k ∈ unvisit [ τ i k ( t ) ] α [ η i k ] β , j ∈ unvisit k 0 , else η i j = 1 d i j p_{ij}^k(t)=\begin{cases} \frac{\left[\tau_{ij}(t)\right]^\alpha\left[\eta_{ij}\right]^\beta}{\sum_{k\in\text{unvisit}}\left[\tau_{ik}(t)\right]^\alpha\left[\eta_{ik}\right]^\beta},&j\in\text{unvisit}_k\\ 0,&\text{else}\end{cases} \\ \eta_{ij} = \frac{1}{d_{ij}} pijk(t)={∑k∈unvisit[τik(t)]α[ηik]β[τij(t)]α[ηij]β,0,j∈unvisitkelseηij=dij1
其中:
- t t t: 迭代次数
- k k k: 第k只蚂蚁;
- i i i: 当前所在节点i;
- j j j: 下一个节点j;
- τ i j \tau_{ij} τij: 信息素
- η i j \eta_{ij} ηij: 启发值,实际是两个节点的距离倒数,即距离越小,往该节点的前进的概率越大;
- α \alpha α: 信息素的权重因子
- β \beta β: 启发值的权重因子
根据上式,不难发现两个权重因子直接影响着蚂蚁每一步的决策,
α
\alpha
α 过大会导致蚂蚁倾向走之前的路,搜索其它路径的趋势减小,容易陷入局部最优就难以再逃脱;相反,
β
\beta
β 过大就越倾向于贪心算法,只往当前节点的最小值走.
有了以上节点的概率以后,只需要模拟该概率分布情况做一次采样即可,具体可使用轮盘赌法形式来选择,所谓轮盘堵法是,已知各个选择的概率,每个概率代表在单位长度上所占据的区域长度,然后在该单位长度上随机生成一个数,该值落在哪个区间则选择该节点.程序的实现可以使用cumsum:
probabilities = np.zeros(len(unvisit))
for k in range(len(unvisit)):
probabilities[k] = np.power(pheromonetable[visiting][unvisit[k]], alpha) * \
np.power(eta[visiting][unvisit[k]], beta)
# 使用轮盘赌选择下一个节点
# 累计概率
cumsum = (probabilities / sum(probabilities)).cumsum()
cumsum -= np.random.rand()
# 求出随机值处于哪个概率区间
next = unvisit[list(cumsum > 0).index(True)]
3.2 信息素更新
每只蚂蚁根据上面的规则选择路径后,即各自得到一条路径,这时候需要更新信息素(相当于总结归纳经验),以此来引导后面迭代蚂蚁的选择.具体的更新如下:
τ i j ( t + 1 ) = ( 1 − p ) τ i j ( t ) + Δ τ i j Δ τ i j = ∑ k = 1 m Δ τ i j k \tau_{ij}(t+1) = (1-p)\tau_{ij}(t) + \Delta \tau_{ij} \\ \Delta \tau_{ij} = \sum_{k=1}^{m} \Delta \tau_{ij}^k τij(t+1)=(1−p)τij(t)+ΔτijΔτij=k=1∑mΔτijk
其中,
- Δ τ i j k \Delta \tau_{ij}^k Δτijk: 第k只蚂蚁在节点i与节点j连接路径上释放的信息素浓度;
- Δ τ i j \Delta \tau_{ij} Δτij: 所有蚂蚁在节点i与节点j连接路径上释放的信息素浓度总和;
- p p p: 信息素浓度的挥发率,很直观,就是衡量上一次迭代信息素浓度的保留程度
每只蚂蚁在每个节点连接处增加的信息有3种方法:
- 蚁周模型
- 蚁量模型
- 蚁蜜模型
直接引用上面博客中的描述
| 信息素增量不同 | 信息素更新时刻不同 | 信息素更新形式不同 | |
|---|---|---|---|
| 蚁周模型 | 信息素增量为 Q / L k Q/L_k Q/Lk,它只与搜索路线有关与具体的路径(i,j)无关 | 在第k只蚂蚁完成一次路径搜索后,对线路上所有路径进行信息素的更新 | 信息素增量与本次搜索的整体线路有关,因此属于全局信息更新 |
| 蚁量模型 | 信息素增量为 Q / d i j Q/d_{ij} Q/dij,与路径(i,j)的长度有关 | 在蚁群前进过程中进行,蚂蚁每完成一步移动后更新该路径上的信息素 | 利用蚂蚁所走路径上的信息进行更新,因此属于局部信息更新 |
| 蚁密模型 | 信息素增量为固定值Q | 在蚁群前进过程中进行,蚂蚁每完成一步移动后更新该路径上的信息素 | 利用蚂蚁所走路径上的信息进行更新,因此属于局部信息更新 |
下面的程序将以 蚁周模型 方式更新信息素
3.3 算法实现
经过上面介绍,利用蚁群算法求解TSP问题伪代码可总结如下
初始化参数:建立距离表;设置权重因子;初始化信息素;初始化启发值;设置挥发系数
迭代开始:
将m只蚂蚁随机投放到节点中
为每只蚂蚁生成路径:
选择下一节点直至全部访问:
根据当前所在节点和选择下一节点的概率,随机选取下一节点
计算路径总长度
更新最优路径
更新信息素
输出路径
def SolveTspByAC(nodes, ants = 100, maxIter = 200):
"""
@brief:Ant Colony 蚁群算法 解决大规模的TSP问题
"""
numNode = len(nodes)
distances = np.zeros((numNode, numNode))
for i in range(numNode):
for j in range(numNode):
if i == j:
distances[i][j] = 1e10
else:
# 根据输入的数据结构计算两个节点的距离
distances[i][j] = (nodes[i] - nodes[j]).norm()
# 启发矩阵
eta = 1.0 / distances
# 信息素
# 信息素权重因子
alpha = 1
# 启发函数权重因子
beta = 2
rho = 0.1
# 单只蚂蚁一条路径的信息素总和
Q = 1
# 信息素矩阵
pheromonetable = np.ones((numNode, numNode))
minLenght = 1e10
for iter in range(maxIter):
# 记录每只蚂蚁的路径
paths = np.zeros((ants, numNode), dtype=np.int32)
# 为每一只蚂蚁选择初始点
if ants <= numNode:
paths[:, 0] = np.random.permutation(range(numNode))[:ants]
else:
paths[:numNode, 0] = np.random.permutation(range(numNode))[:]
paths[numNode:, 0] = np.random.permutation(range(numNode))[: (ants - numNode)]
# 记录每只蚂蚁的路径总长
lengths = np.zeros(ants)
for i in range(ants):
unvisit = list(range(numNode))
visiting = paths[i][0]
unvisit.remove(visiting)
for j in range(1, numNode):
probabilities = np.zeros(len(unvisit))
for k in range(len(unvisit)):
probabilities[k] = np.power(pheromonetable[visiting][unvisit[k]], alpha) * \
np.power(eta[visiting][unvisit[k]], beta)
# 使用轮盘赌选择下一个节点
# 累计概率
cumsum = (probabilities / sum(probabilities)).cumsum()
cumsum -= np.random.rand()
# 求出随机值处于哪个概率区间
next = unvisit[list(cumsum > 0).index(True)]
paths[i, j] = next
unvisit.remove(next)
lengths[i] += distances[visiting][next]
visiting = next
# 最后一个节点和第一个节点的距离也加上 是否必须?
lengths[i] += distances[visiting][paths[i, 0]]
# 更新最优路径
if minLenght > lengths.min():
minLenght = lengths.min()
bestPath = paths[lengths.argmin()].copy()
# 更新信息素
delta = np.zeros((numNode, numNode))
# for i in range(ants):
# for j in range(numNode-1):
# delta[paths[i, j]][paths[i, j+1]] += (Q / lengths[i])
# # 最后一个节点与第一个节点同样需要更新
# delta[paths[i, -1]][paths[i, 0]] += (Q / lengths[i])
for i in range(ants):
for j in range(numNode-1):
delta[paths[i, j]][paths[i, j+1]] += (Q / distances[paths[i, j]][paths[i, j+1]])
# 最后一个节点与第一个节点同样需要更新
delta[paths[i, j+1]][paths[i, 0]] += (Q / distances[paths[i, j+1]][paths[i, 0]])
pheromonetable = (1-rho) * pheromonetable + delta
return bestPath
需要注意的是:上面的实现,根据蚁周模型的更新公式,应该对应的是注释了的部分,但是实测发现收敛速度没有未注释的快,而未注释没有找到相关依据,只是参考了博客中如此实现,没有深入考究,但直观上还是说得通.























 3450
3450

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








