轮胎侧向力MATLAb建模
基于“魔术公式”的轮胎动力学仿真分析”
01 魔术轮胎的统一形式为:
魔术公式”采用三角函数的组合公式拟合实验轮胎数据,用一套形式相同的公式就可以完整的表达纵向力、侧向力、回正力矩、反转力矩、滚动阻力以及纵向力、侧向力联合作用的工况魔术 公 式 统一性强,需要拟 合 的 参 数 都 有 明 确 的 物 理 意 义,容易确定初值。并且由于魔术公式是基于试验数据,处在试验的范围的高精度外,甚至在极限值以外的一定程度也可使用,它拟合精度高,但计算量大,因此更适用于产品设计、汽车动态模拟及试验对比等要求精确描述轮胎力学特性的领域。

02 纯转弯工况下的拟合参数
轮胎的侧偏特性是轮胎力学特性的一个重要组成部分,侧偏特性主要是指侧偏力、回正力矩与侧偏角的关系,忽略了回正力矩的影响,针对侧偏力与侧偏角的关系进行了仿真分析。当轮胎处于一边滚动一边侧滑状态时,在轮胎上会发生摩擦力。此摩擦力在轮胎侧向的分力是侧向力,切向的分力是滚动阻力,在与轮胎前进方向成直角的分力为侧偏力,而在前进方向的分力是侧偏阻力。由于滚动阻力较小,且随着侧偏角没有太大的变化,故可以略而不计。因此在侧偏角小的情况下,侧向力和侧偏力大体上可以看作是同样的值。



3 分析公式
step1 查看魔术轮胎公式里的未知量:
1:X:侧偏角或者纵向滑移率。
2:Fz: 垂直载荷。
3:车轮的外倾角,一般给0;
4 搭建模型
4.1 选取matlab函数模块,在里面编写魔术轮

4.2 函数代码
// An highlighted block
function y = fcn(u1,Fz,roll)
% u1为前轮侧偏角或者纵向滑移率。
% Fz为垂直载荷。
% roll为车轮的外倾角。
a1 =-221.1;
a2 =1011;
a3 = 1078;
a4 = 1.82;
a5 = 0.208;
a6 =0;
a7 = -0.354;
a8 =0.707;
a9 = 0.028;
a10 = 0;
a11 = 14.8;
a12 = 0.022;
C = 1.3;
D = (a1*Fz^2+a2*Fz);
BCD = a3*sin(a4*atan(a5*Fz)*(1-a12*abs(roll)));
B = BCD/(C*D);
E = a6*Fz^2+a7*Fz+a8;
Sh = a9*roll;
Sv = (a10*Fz^2+a11*Fz)*roll;
x = u1+Sh;
y = D*sin(C*atan(B*x-E*(B*x-atan(B*x))));
Fy = -(y+Sv);
4.3 给出侧偏角的范围

由图可知:
01 轮胎的侧偏角在 :0°~20°
给一个线性的信号,使用simlink的“ramp”模块;设置斜率为1;仿真时间设置为20s;
02 给出载荷1KN、3KN、5KN、7KN。
使用constant常量模块;

03 给出roll 的值,为:0;
5 魔术轮胎框图
1KN载荷下的侧向力
负的侧偏角,正的侧偏力。正的侧偏力,负的侧偏角。



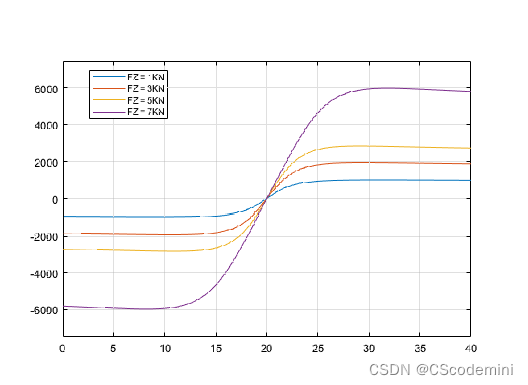









 文章介绍了如何使用MATLAB进行轮胎侧向力的建模分析,基于‘魔术公式’对轮胎动力学进行仿真,重点在于纯转弯工况下侧偏力的拟合参数。在建模过程中,设置了不同的侧偏角、垂直载荷和车轮外倾角值,通过MATLAB函数模块编写代码来计算侧向力。
文章介绍了如何使用MATLAB进行轮胎侧向力的建模分析,基于‘魔术公式’对轮胎动力学进行仿真,重点在于纯转弯工况下侧偏力的拟合参数。在建模过程中,设置了不同的侧偏角、垂直载荷和车轮外倾角值,通过MATLAB函数模块编写代码来计算侧向力。
















 573
573

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








