神经网络简介

导语

书中已经表明感知机理论上可以表达任意的复杂函数（感知机简介），但问题是，对于一个已经做好框架的感知机，如何通过确定参数使得其能够实现函数想要的功能，在神经网络诞生之前，这些权重参数大多是人工设定的，神经网络的出现解决了自动从数据中学习权重参数的问题。

在学习神经网络如何自动学习之前，需要搞清楚神经网络的结构，以及神经网络是如何实现预测的，神经网络是如何在感知机的基础上优化的，书上的神经网络这一章详细的介绍了这些。

感知机与神经网络

神经网络一般分为三部分，输入层，隐藏层（该层可能有多层），输出层，如下图，其实和感知机没太大区别，具体的区别还是在内部的实现上。

感知机的概念和图见（感知机简介），这里不作赘述。
在感知机的式子当中，是存在偏置值b的，但是一般的图中没有加上它，如果我们把b也作为输入考虑进来的话，感知机的表示就会变成下图。

为了表示的更简单，书上将判断式子$b+w_1{x}_1+w_2{x}_2$视为了一个整体，引入新函数$h(x)$，得到式子$y=h(b+w_1{x}_1+w_2{x}_2)$，这里的$h(x)$是一种判断函数，具体如下。

$$h(x)=\{\begin{array}{llc}0,& if& (x\le 0)\\ 1,& if& (x>0)\end{array}$$

这里的$h(x)$也可以取别的函数。

激活函数

上文所提到的$h(x)$，作用是将输入信号总和转换为输出信号，即激活函数。在感知机的基础上，神经网络将信号总和与阈值判断分离开，设信号总和为$a$，那么就可以得到$a=b+w_1{x}_1+w_2{x}_2,y=h(a)$，激活函数的作用方式具体如图。

有了激活函数，感知机就真正的迈向了神经网络，对于感知机来说，其激活函数是阶跃函数，如果把阶跃函数换成别的函数，就是神经网络了。由于不同的需求，因而诞生了许多不同的激活函数。

sigmoid

这里只简单给出函数式、图像和实现，其他的函数也一样。

函数式：$h(x)=\frac{1}{1+e^{-x}}$

图像：

函数实现：

def sigmoid(x):
	return 1/(1+np.exp(-x))

阶跃函数

函数式：$$h(x)=\{\begin{array}{llc}0,& if& (x\le 0)\\ 1,& if& (x>0)\end{array}$$

图像：
函数实现：

def step_function(x):
	if x>0:
		return 1
	else :
		return 0

ReLU

函数式：$$h(x)=\{\begin{array}{llc}0,& if& (x\le 0)\\ x,& if& (x>0)\end{array}$$

图像：

函数实现：

def relu(x):
	return np.maximum(0,x)

线/非线性函数

根据书中的定义，线性函数指输出值是输入值常数倍的函数，图像上的表达是一条笔直的直线，非线性函数与之对应，指不像线性函数那样图像表达是一条直线的函数，上述提到的激活函数都是非线性函数。

神经网络的激活函数必须使用非线性函数，如果使用线性函数的话，神经网络的层数就变得没有意义了，可以这样理解，如果用线性函数来表达神经网络的话，假设每一层的参数是$a_1,a_2,......,a_n$，函数表达式就会变成$y(x)=h(.....(x)......)$，其实可以直接转换成$y(x)=h^{\prime }(x),h^{\prime }(x)=a_1{a}_2......a_{n}x$，只需要一层就可以表达（书上说法：不管层数多少，总是存在与之等效的“无隐藏层的神经网络”），这样无法发挥多层神经网络的特点，因此必须使用非线性函数。

简单神经网络实现

书上给出了一些简单神经网络以及实用的例子，不过这只包含了推导的部分，不包含学习的部分，其中涉及到矩阵乘法的部分属于线性代数的基本常识，因此略过，没有记录。

3层神经网络实现

书上的神经网络采用numpy实现，激活函数选取sigmod，一共三层，粗略图和详细图分别如下。

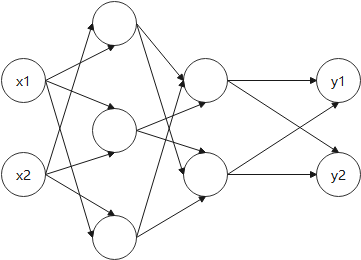
用矩阵的乘法运算来表示：$A^i=X{W}^i+B^i，Z^i=sigmoid(A^i)$，其中，$A$为该层的总和，$X$为输入，$W$为权重，$B$为偏置，$Z$为输出（实现代码均来自原书，我只是更改了一点数据）。

第一层实现如下（加上了激活函数）：

X=np.array([0.5,0.7])
W1=np.array([[0.1,0.2,0.3],[0.4,0.5,0.6]])
B1=np.array([0.1,0.2,0.4])
A1=np.dot(X,W1)+B1
Z1=sigmoid(A1)

一、二层间信号传递（加了激活函数）：

W2=np.array([[0.2,0.5],[0.1,0.8],[0.4,0.7]])
B2=np.array([0.4,0.2])
A2=np.dot(Z1,W2)+B2
Z2=sigmoid(A2)

二层到输出层信号传递（加了激活函数）

W3=np.array([0.3,0.5],[0.1,0.6])
B3=np.array([0.9,0.3])
A3=np.dot(Z2,W3)+B3
Y=identity_function(A3)

合并成一个整体：

import numpy as np

def sigmoid(x):
	return 1/(1+np.exp(-x))

def identity_function(x):
    return x

def init_network():#对权重和偏置初始化
    network={}
    network['W1']=np.array([[0.1,0.2,0.3],[0.4,0.5,0.6]])
    network['b1']=np.array([0.1,0.2,0.4])
    network['W2']=np.array([[0.2,0.5],[0.1,0.8],[0.4,0.7]])
    network['b2']=np.array([0.4,0.2])
    network['W3']=np.array([[0.3,0.5],[0.1,0.6]])
    network['b3']=np.array([0.9,0.3])
    return network

def forward(network,x):#前向函数，表示输入到输出方向的传递处理
    W1,W2,W3=network['W1'],network['W2'],network['W3']
    b1,b2,b3=network['b1'],network['b2'],network['b3']

    a1=np.dot(x,W1)+b1
    z1=sigmoid(a1)
    a2=np.dot(z1,W2)+b2
    z2=sigmoid(a2)
    a3=np.dot(z2,W3)+b3
    y=identity_function(a3)

    return y

network =init_network()
x=np.array([0.5,0.7])
print(forward(network,x))

输出结果如图：

输出层

神经网络大多用于分类或者回归问题上，根据不同的情况采取不同的激活函数，一般分类用恒分函数，回归用softmax函数。

分类问题应用场景通常是给出多组图片，例如一堆猫狗，然后判断每张图片是猫是狗，回归问题应用场景通常是给出一些已经拿到的数据，例如01到22年房地产价格，要预测23年价格。

恒等函数

恒等函数是直通的，输入什么，输出就是什么，在输出层使用恒等函数时，输入信号会原封不动输出，具体如图。

softmax

分类问题中的softmax函数的表达式为$y_k=\frac{e^{a_k}}{{\sum }_{i=1}^n{e}^{a_i}}$，可以判断出，softmax函数的输出永远都位于0~1之间，因此可以将其输出视为概率，在神经网络中，一般认为输出值最大的神经元对应的类别为网络的识别结果，即使再使用一次softmax，相对的大小结果也是不会变的，因此输出层的softmax函数一般被省略了。

softmax的表示图如下：

python的实现如下：

import numpy as np
def softmax(a):
    exp_a=np.exp(a)
    return exp_a/np.sum(exp_a)

式子很简单，也易于理解，我们可以分别取$a_k=1,10,100,\mathrm{1000......}$等数据带入算一下，当带入到100及以上的时候，可以发现$e^{a_k}$变成一个很大的数字，很难表达，而基于这样一个值的运算更是天方夜谭，softmax的使用到这里似乎陷入了停滞。

基于对数函数的性质，书上给出了这样一个计算的优化，过程如下：
$$\begin{array}{rl}{y}_k& =\frac{exp(a_k)}{{\sum }_{i=1}^{n}exp(a_i)}\\ & =\frac{Cexp(a_k)}{C{\sum }_{i=1}^{n}exp(a_i)}\\ & =\frac{exp(a_k+lnC)}{{\sum }_{i=1}^{n}exp(a_i+lnC)}\\ & =\frac{exp(a_k+C^{\prime })}{{\sum }_{i=1}^{n}exp(a_i+C^{\prime })}\end{array}$$

也就是说同时对所有的$a_k$加上或减去一个常数，不会影响最后的结果，为了方便，一般是减去所有输入信号的最大值。

于是python的表达就变成了：

import numpy as np
def softmax(a):
    exp_a=np.exp(a-np.max(a))
    return exp_a/np.sum(exp_a)

手写数字识别（仅前向传播）

书上在这章仅仅讲述了神经网络的推理，也就是在已经学习到参数的基础上，对输入的数据进行预测。

读入和显示

数据集采用MNIST手写数字图像集，源码和数据集请参考深度学习入门-基于Python的理论入门与实现源代码加mnist数据集下载推荐给出的链接，如果直接用源码来下载数据集的话八成下不下来。

这里并不剖析源码中mnist.py的部分，只简单解释下与读入和展示相关的代码。

读入数据使用mnist.py中的load_mnist()函数，函数代码如下：

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集
    
    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label : 
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组
    
    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):#如果不存在，直接重新运行
        init_mnist()
        
    with open(save_file, 'rb') as f:#加载对应路径的文件
        dataset = pickle.load(f)##构造数据集
    
    if normalize:#如果要规格化
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    if one_hot_label:#采用onehot模式
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
    
    if not flatten:#判断是否变为一维
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])#返回每个数据集对应生成的信息 

函数以（训练图像，训练标签）（测试图像，测试标签）的键值对形式返回读入数据。

对于读入数据的展示代码如下：

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image

def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)#按照格式返回数据集

img = x_train[1]#拿第一个尝试展示
label = t_train[1]
print(label)  # 5

print(img.shape)  # (784,)
img = img.reshape(28, 28)  # 把图像的形状变为原来的尺寸
print(img.shape)  # (28, 28)

img_show(img)

执行结果：

推理处理

每个图像均为28×28的像素，考虑到要对每个像素输入，所以神经网络的输入层应有784个神经元，最后要对图像进行0~9的分类，所以输出层应该有10个神经元，书上给出的神经网络有2个隐藏层。

首先给出书上读入数据和预测的代码：

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test#拿到测试集

def init_network():#获得初始化的神经网络参数
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network

#pickle把运行中的对象保存成文件，加载则可恢复

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']#参数赋值
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)#传播过程

    return y

x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])#对第i个图片进行预测
    p= np.argmax(y) # 获取概率最高的元素的索引，视为预测结果
    if p == t[i]:
        accuracy_cnt += 1

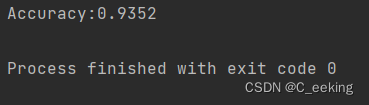
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

运行结果：

批处理

将许多组数据打包，作为单次输入的数据，这样的一组数据就是批，一般来说，批处理的会比分开逐步计算各个小型数组快，可以按照流水线的原理理解。

按照批处理的思想，将预测的代码可以改成如下：

batch_size = 100 # 批数量
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]#拿100个图片
    y_batch = predict(network, x_batch)#一次性预测一百张
    p = np.argmax(y_batch, axis=1)#生成一个最大值数组
    accuracy_cnt += np.sum(p == t[i:i+batch_size])#最大值数组与正确值一一比较

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

总结

神经网络的构造看起来很复杂，但是如果一步一步实现的话，其实也并不是什么难事，代码中体现的数学原理最多也就到矩阵相乘，还是挺容易理解的。

参考文献

1. 《深度学习入门——基于Python的理论与实践》
2. 深度学习入门-基于Python的理论入门与实现源代码加mnist数据集下载推荐