目录
Basic Iterative Method & Iterative Least-Likely Class method
本文结合了论文Adversarial Examples: Attacks and Defenses for Deep Learning以及课程Reliable and Interpretable Artificial Intelligence,是神经网络对抗性自己的一个整理,未完。
简介
“Adversarial examples are inputs to machine learning models that an attacker has intentionally designed to cause the model to make a mistake”
(Goodfellow et al 2017)
神经网络对抗性样本的案例
在语义分割分割中,向图像添加扰动,使得神经网络无法识别人像

在stop标志上贴上黑白条,自动驾驶系统将其识别成为45迈的标志

对抗样本在很多领域都有应用,例如:
- 人脸识别(Face Recognition)
- 强化学习(Reinforcement Learning)
- 模型生成(Generative Modeling)
- 物体检测(Object Detection)
- 语义分割(Semantic Segmentation)
- 自然语言处理(Natural Language Processing,NLP)
- 恶意软件检测(Malware Detection)
神经网络的鲁棒性
Robustness: A network is robust if it returns correct output on all inputs
定义:一个神经网络的鲁棒性是指能够对所有的输入均返回正确的结果
很明显,这个定义有些不太切合实际,因为输入空间实在太大了,不可能做到全部覆盖
Local Robustness (informal): A learning model is locally-robust if it returns the correct output on inputs similar to inputs in the training set
局部鲁棒性的定义是对于学习模型来说,如果输入与训练数据集相似的数据,能够返回正确的结果,就可以说该模型具有局部鲁棒性
为什么神经网络仅拥有高精确度是不够的?
- 训练和测试集中的输入来自给定的分布,神经网络旨在从给定分布中得出的测试集上实现高精度,但仍然有许多相似的输入从未经过测试(对于给定的分布,概率很低)
- 另一点是神经网络可能学习了无关紧要的特征作为判断的依据,一旦出现一些轻微的扰动,神经网络就会出现判断错误
为什么会存在对抗样例?
神经网络太过于线性
神经网络有激活层为之增添非线性,但激活函数仍然有些部分是线性的,例如这个阶跃函数,x<0和x>0的部分分别为两个线性函数

即使是sigmoid函数,中间红线标出的部分也是很接近线性的

为什么神经网络的激活函数要设计的如此"线性"呢?因为这样比较方便优化
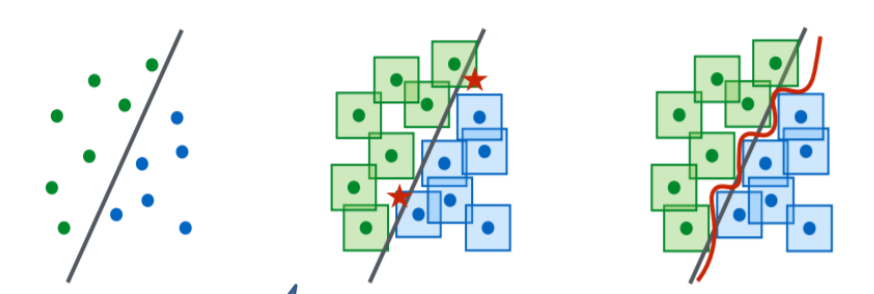
我们采用示例模型对这个问题进行解释,左边这张图模拟了一个神经网络的接近线性的分类器,它将点分成了两个部分,第二张图,这些点周围的方形区域行成了与这些点相似的数据,我们认为这些区域的数据如果输入神经网络中应该得到与训练数据相同的结果,但是我们看到图中标注五角星的地方,这些区域出现了分类的错误,这些样本我们就可以称为对抗样本,所以线性的分类器对于分类来说不够强大,如果我们将对抗样本添加入训练数据集让神经网络重新训练,现在的分类器就如同第三张图的红线所示,它拥有了更高的准确性。
生成对抗样本的方法分类
生成对抗样本的方法我们将它分为三个维度,分别是模型威胁(threat model),扰动(perturbation),基准(benchmark)
A 模型威胁(threat model)
从对抗性伪造(False positive attacks)角度来看:
- 假正例攻击(False Positive Attacks)
生成一个反例,但是模型误将其分类为正例
- 假反例攻击(False Negative Attacks)
和前面相反,生成一个正例,但是模型误将其分类为反例
从攻击者的知识(Adversary’s Knowledge)来看
-
白盒测试(White-box)
攻击者了解他们正在攻击的神经网络的架构和参数
-
黑盒测试(black-box)
攻击者不能访问神经网络,只能知道被攻击模型的输出(标签和置信度)
这两类和可以类比软件工程的白盒黑盒,就在于攻击者知不知道神经网络的内部结构
对抗性(Adversarial Specificity)来看
- 有针对性的攻击(target)
生成的对抗样本被模型误分类为某个指定的分类,这种一般发生在多目标分类中
- 没有针对性的攻击(Non-targeted)
只要攻击成功就好,和分类为哪个类别没有关系。因为无目标攻击具有更大的输出范围,因此比目标攻击更容易实现。
攻击频率(Attack Frequency)
-
一次性攻击(One-time attacks)
生成对抗样本时优化一次
-
迭代攻击(Iterative attacks)
生成对抗样本时需要更新多次
与一次性攻击相比,迭代攻击通常会执行更好的对抗示例,但需要与受害者分类器进行更多交互(更多查询),并且花费更多的计算时间来生成它们。 对于某些计算量大的任务(例如强化学习),一次性攻击可能是唯一可行的选择。
B. 扰动(perturbation)
扰动范围(Perturbation Scope)
-
个别攻击(Individual attacks)
为每个正例输入产生不同的扰动
-
通用攻击(Universal attacks)
只会对整个数据集产生通用扰动。此扰动可应用于所有干净的输入数据。
扰动限制(Perturbation Limitation)
-
优化扰动(Optimized Perturbation)
将扰动设置为优化问题的目标。 这些方法旨在最小化扰动,以使人类无法识别扰动。
-
约束扰动(Constraint Perturbation)
约束扰动将扰动设置为优化问题的约束。 这些方法只要求扰动足够小
C. 基准测试(BenchMark)
从基准测试维度,就是根据数据集和被攻击的模型进行分类
-
数据集(datasets)
MNIST, CIFAR-10和ImageNet
-
受害模型(Victim Models)
LeNet, VGG, AlexNet, GoogLeNet, CaffeNet, and ResNet
通常来说,大型和高质量的数据集、复杂和高性能的深度学习模型通常会使对手/防御者难以攻击/防御
生成对抗样本的具体方法
生成对抗样本,我们的做法是为输入x添加一个扰动η,对于神经网络代表的函数f,要求f(x)=y,即输入为x时输出为正确的标签,而f(x+η)=y',即添加扰动后,输出错误标签,同时我们要求这个扰动η尽可能的小,要让人分辨不出来。
用形式化的语言描述一下这个过程:

这个代表η的Lp范数(norm),范数概念不在这里描述。
L-BFGS Attack
这个方法来自于2014年的一篇论文,是对抗样本(adversarial examples)领域的开山之作,我们希望f(x+η)被错误分类,同时保证x+η在[0,1]之间(保证是一张合法的图片),直接解这个问题不容易,因此作者换了一种思路,从损失函数的角度寻找最优,把问题转化为求最小值。

而L-BFGS attack就是用L-BFGS算法来线性搜索上面这个这个式子的最小值。
快速梯度正弦法(FGSM)
无针对性的快速梯度正弦法(Untargeted Fast Gradient Sign Method)
假设现在我们有一张图片x,由一个高维向量表示,xi代表这张图片的第i个像素,它的label为y(y为正确的标签),模型的参数我们用θ表示,它表示的含义为如果图像的数据沿着这个方向进行变化,那么它的变化,相对于其他方向而言,对目标函数值的影响是最大。

这个地方是计算x,y点处的梯度,
代表一个很小的数,例如0.0007
sign函数表示为:

因为计算梯度时不同的方向维度的梯度幅度不同,这个sign函数就是当向量某个维度的值小于0的时候让它等于-1,>0的时候让它等于1,例如(0.1,0,-0.2)输入sign就变成(1,0,-1)。在生成数据时,各个方向被统一归一化成相同的数量,这样就可以确保在修改图片时,每个像素的修改量尽量相同,修改得更均匀些。
可以看到第二步中,x'=x+η,因为我们的目标是输出一个不正确的标签,所以要做出远离(get away)正确标签的动作,用的是+符号
第三步中,因为这里是无针对性(untargeted)的,所以只要让输出标签不正确就行了,不用管输出了啥标签,检查的是f(x')≠y
有针对性的快速梯度正弦法(targeted Fast Gradient Sign Method)

带有针对性,它与没有针对性的区别在于,它这里使用的y’是目标的错误标签,值得注意的是,这里的符号是减号,这代表朝着偏向标签y’的方向移动
最后,FGSM被设计为快速产生对抗样本,但它并不能保证产生的扰动是最小的。
使用FGSM的一个例子就是,将一张熊猫图片加入扰动之后,被识别成了长臂猿

FGSM还有其他的变种
Fast Gradient Value (FGV),扰动的求值方式为,也就是少了sign函数,可以生成局部差异较大的图像。
RAND-FGSM (R-FGSM),增加随机梯度训练,用于防御对抗训练
Basic Iterative Method & Iterative Least-Likely Class method
Basic Iterative Method (BIM)是基本迭代法,Kurakin等人扩展了快速梯度符号法,通过运行一个更精细的优化(较小的变化)多次迭代。在每次迭代中,它们都会剪裁像素值,以避免每个像素发生较大变化

Clip函数,限制一个array的上下界,例如给出上下界[0,1]如果数组中的元素值<0则另值为0,如果>1,则另值为1
BIM是一种没有针对性的攻击
Iterative Least-Likely Class method(ILLC)是一种有针对性的攻击方法,为了进一步攻击特定的类,他们选择了预测中可能性最小的类,并试图最大化交叉熵损失。这种方法被称为迭代最不可能类方法
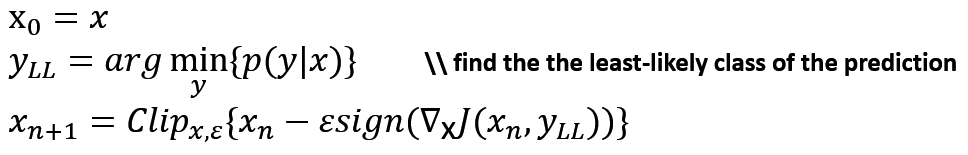
DeepFool
DeepFool: a simple and accurate method to fool deep neural networks
DeepFool寻找从原始输入到对抗性例子决策边界的最近距离,为了克服高维中的非线性,他们采用线性近似进行迭代攻击。

采用的算法我个人理解是,随机选个点,按照它梯度上升的方向进行迭代,直到标签产生变化,迭代过程中移动的距离之和就是该输入到决策边界的距离,这样就可以找到距离决策边界最近的点,以及相应的攻击用标签。
这个算法属于untarget attack,并且该算法产生的扰动非常小。

对比FGSM和DeepFool,我们可以明显地看到,DeepFool产生的扰动比FGSM小得多。
Universal Perturbation
这个方法和DeepFool类似,不过它是针对于所有的图像,仍然迭代搜索最小的扰动,直到找到一个扰动,使得对于大多数样本使用这个扰动,能够欺骗到神经网络为止。
C&W Attack
引自论文“Towards Evaluating the Robustness of Neural Networks”,作者是Nicholas Carlini & David Wagner,攻击方法名字中的C和W就是这么来的
起因同样是f(x+η)这个是个离散条件,很难计算,作者定义了函数obj(x+η),使得当且仅当obj(x+η)≤0时条件成立。
于是问题转化为了求解的最小值

作者在论文里面给出了7中满足条件的函数,作者认为其中一种比较有效的是6

作者使用了新变量w,使得w满足以避免box的约束
于是对于L2范数的攻击可以描述为:

CPPN EA Fool
这是一种假阳性攻击,如下图,生成虚假的噪声图片,让神经网络识别为正常的样本,使用的是进化算法(EAs)来生成对抗样本,通过该方法产生的对抗样本会被DNNs以99%的置信度进行误分类。

One Pixel Attack
这是一种黑盒攻击,不需要知道梯度和神经网络参数的任何信息,是一种比较极端的攻击方法,每次只改一个像素,利用差分进化(DE)(一种进化算法)来找到最优解。
Others
- Zeroth Order Optimization
- Jacobian-based Saliency Map Attack (JSMA)
- Hot/Cold
- Natural GAN
- Model-based Ensembling Attack
- Ground-Truth Attack
- Projected gradient descent(PGD)
- Diffing Networks
























 2861
2861

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








