1、对称矩阵
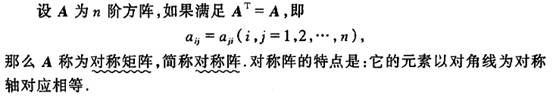
2、转置矩阵

3、Hermite矩阵
4、复共轭转置

Hermite阵是对称阵概念的推广,对称阵针对实矩阵(矩阵元素均为实数),Hermite阵针对复矩阵。
5、正交矩阵

6、酉矩阵
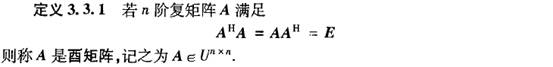
类似于Hermite阵相对于对称阵,酉矩阵是正交阵概念的推广。
7、奇异矩阵

8、正规矩阵

9、幂等矩阵

10、可逆矩阵
定义:
设A是数域上的一个n阶方阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=I。 则我们称B是A的逆矩阵,而A则被称为可逆矩阵。
可逆条件:
A是可逆矩阵的充分必要条件是,即可逆矩阵就是非奇异矩阵。(当 时,A称为奇异矩阵)
时,A称为奇异矩阵)
性质:
- 矩阵A可逆的充要条件是A的行列式不等于0。
- 可逆矩阵一定是方阵。
- 如果矩阵A是可逆的,A的逆矩阵是唯一的。
- 可逆矩阵也被称为非奇异矩阵、满秩矩阵。
- 两个可逆矩阵的乘积依然可逆。
- 可逆矩阵的转置矩阵也可逆。
- 矩阵可逆当且仅当它是满秩矩阵。


伪逆矩阵:
伪逆矩阵是逆矩阵的广义形式。由于奇异矩阵或非方阵的矩阵不存在逆矩阵,但在matlab里可以用函数pinv(A)求其伪逆矩阵。基本语法为X=pinv(A),X=pinv(A,tol),其中tol为误差,pinv为pseudo-inverse的缩写:max(size(A))*norm(A)*eps。函数返回一个与A的转置矩阵A' 同型的矩阵X,并且满足:AXA=A,XAX=X.此时,称矩阵X为矩阵A的伪逆,也称为广义逆矩阵。pinv(A)具有inv(A)的部分特性,但不与inv(A)完全等同。 如果A为非奇异方阵,pinv(A)=inv(A),但却会耗费大量的计算时间,相比较而言,inv(A)花费更少的时间。
伪逆矩阵求法:
A 为m*n矩阵,r代表矩阵的秩:
若矩阵A是方阵,且|A|!=0,则存在AA-1=E;
若A不是方阵,或者|A|=0,那么只能求A的伪逆,所谓伪逆是通过SVD计算出来的;
pinv(A)表示A是伪逆:
如果A列满秩,列向量线性无关,r=n,Ax=b为超定方程组,存在0个或1个解,那么 ,因为
,因为 ,因此也称为左逆;
,因此也称为左逆;
如果A行满秩,行向量线性无关,Ax=b为欠定方程组,存在0个或无穷个解,那么 ,因为
,因为 ,因此也称为右逆;
,因此也称为右逆;
如果秩亏损,那么只好先做奇异值分解 ,U,V是正交阵,D是对角阵;然后取对角阵S,如果D(i,i)=0,那么S(i,i)=0,如果D(i,i)<>0,那么S(i,i)=1/D(i,i)。于是
,U,V是正交阵,D是对角阵;然后取对角阵S,如果D(i,i)=0,那么S(i,i)=0,如果D(i,i)<>0,那么S(i,i)=1/D(i,i)。于是 ;
;
主要内容:
-
什么是最小二乘
-
最小二乘的几何意义
-
正交投影矩阵
什么是最小二乘?
假设我们手上有n组成对的数据,{(xi,yi):i=1…n},为了探究y变量与x变量的关系,我们希望用一个多项式来匹配它,可是多项式中的系数怎么确定呢?拿来拼凑肯定是不行的,最小二乘法告诉我们,这个多项式的系数应该让每个点的误差的平方之和最小。
(百度百科)最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。




最小二乘的几何意义
最小二乘的几何意义:最小二乘法中的几何意义是高维空间中的一个向量在低维子空间的投影。
从上面的定义中,我们很难想象到最小二乘的几何意义,那么我们通过一个简单的例子来推导一下:

我们根据定义中的误差平方之和最小化来拟合直线:
每个点的误差表示:
最小误差的平方和:
要求解上面的最小化问题,我们可以通过求导的方式得到,最好是转化为矩阵表达形式:AX=b (这里x表示上述的系数a)
求得结果为:

如果通过超定方程的解法 ,很容易就可以得到上面结果。
,很容易就可以得到上面结果。
先来说说向量表达形式:

小括号中表示:它是两个向量 [1, ... , 1]T 和 [x1, ... , xn]T 的线性组合,换句话说,它是这两个向量构成的二维子空间(想成一个平面就可以)的任意一点。
那么上面式子的几何含义:表示向量 [y1, ... , yn]T(表示空间中的一点) 到这个二维子空间任意一点的距离;(向量的长度)
最小化上面式子的平方(向量长度的最小化)的几何含义:寻找在 [1, ... , 1]T 和 [x1, ... , xn]T 构成的二维子空间上的一个点,使得向量 [y1, ... , yn]T 到这个点的距离最小。怎么找这个点呢?只要做一个几何投影就好了。(如下图)

如上图所示,在三维空间中给定一个向量 u,以及由向量 v1,v2 构成的一个二维平面,向量 p 为 u 到这个平面的投影,它是 v1,v2 的线性组合:
利用投影的垂直性质,我们可以得到关于系数C的两个方程:

令 V = [v1, v2], p = c1v1 + c2v2,将上述式子合并并转化为矩阵形式(更容易扩展到高维空间),得到:


因此系数c的表达式为:

有没有发现很熟悉?和式子  一模一样有木有!!!
一模一样有木有!!!
好了,我们回到原来的例子,看看几何关系中的投影点和被投影的空间分别代表什么。
把图中的 u 替换成 [y1, ... , yn]T ,把 v1,v2 分别替换成 [1, ... , 1]T 和 [x1, ... , xn]T, 系数 c1 和 c2 也就是我们要求的 a0,a1。
所以,最小二乘法的几何意义是高维空间的一个向量(由y数据决定)在低维子空间(由x数据以及多项式的次数决定)的投影。
正交投影矩阵
上面提到了最小二乘的几何意义就是空间中的投影,其实投影在线性代数中也是存在其数学公式的,可以联系以下数学知识来理解最小二乘的几何意义。
张成子空间:

张成子空间的投影矩阵:

最小二乘的投影解释:










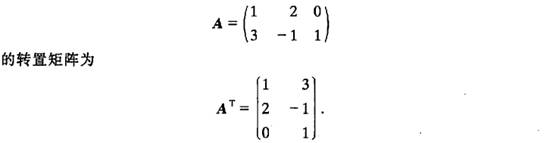
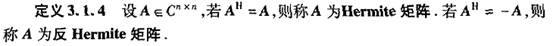
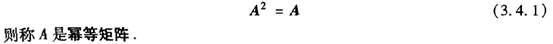














 1564
1564

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








