一个行向量乘以一个列向量称作向量的内积,又叫作点积,结果是一个数;
一个列向量乘以一个行向量称作向量的外积,外积是一种特殊的克罗内克积,结果是一个矩阵,
假设和b分别是一个行向量和一个列向量,那么内积、外积分别记作
和
,,为了讨论方便,假设每个向量的长度为2。
注意:外积在不同的地方定义方式不太一样,这里不详细讨论
定义了内积和外积以后,我们讨论矩阵的乘法。矩阵是由向量组成的,因此对矩阵不同角度的抽象,将矩阵乘法转换为向量乘法,可以使我们从不同的角度去理解矩阵的乘法。首先我们可以对于一个矩阵A(假设行和列的大小都是2),我们可以即可以把它看作由两个行向量组成的列向量,
,又可以看作是由两个列向量组成的行量
,我们
表示列向量,
表示行向量
这样矩阵A和矩阵B的乘积按照不同的角度就可以组成四种理解方式。
一、 A是由行向量组成的列向量,B是由列向量组成的行向量
此时AB乘积变为了两个新的向量的外积形式,按照外积定义,我们有
注意到这里面每一个都是一个向量,因此
就是一个内积,计算结果就是AB矩阵第i行第j列中的元素。因此,我们可以看到,矩阵乘积是两个向量的外积,并且外积矩阵中的每一个元素是一个内积。这种方式是最直接的理解方式。
二、 A是由列向量组成的行向量,B也是由列向量组成的行向量
令C = AB, 我们考虑C的每一个列向量:
同理:
因此,矩阵C的每一个列向量,是A的列向量的一个线性组合,该线性组合中的系数是的各个元素。从这个角度说C的每一列都存在于A的列向量空间内。
三、 A是由行向量组成的列向量,B也是由行向量组成的列向量
类似于上面的情况,不过我们现在考虑C的每一个行向量:
同理:
因此,矩阵C的每一个行向量,是B的行向量的一个线性组合,该线性组合中的系数是的各个元素。从这个角度说C的每一个行向量都存在于B的行向量空间内。
四、 A是由列向量组成的行向量,B也是由行向量组成的列向量
此时AB乘积变为了两个新的向量的内积形式。按照内积定义我们有:
注意到是一个外积形式,因为
是一个列向量,
是一个行向量,因此C是由各个外积矩阵相加得到的。
根据以上分析,我们可以将第一种和第四种方式放到一起,第二种和第三种放到一起分别进行理解。第一种方式先将A抽象为列向量,将B抽象为行向量,从而将矩阵乘法变为了一种外积的形式,而外积矩阵中的每一个元素是一个行向量和一个列向量的内积。这种方式每次得到C的一个元素。
第四种理解方式先将A抽象为行向量,将B抽象为列向量,从而将矩阵乘法变为了一种内积形式,内积的各个组成部分又是一个外积。这种方式每次不是得到C的一个元素
,而是将C看作是多个矩阵相加组成的,每次计算得到一个加数矩阵。
第二种方式将矩阵A、B都抽象为行向量,行向量的每个组成是一个列向量,A乘以B的每一个列向量得到一个新的列向量,并且该列向量存在于A的列向量空间内,A乘以B相当于是对A进行了列变换。第三种方式则将A乘以B看作是对B进行了行变换。
如果想对一个矩阵进行行变换,可以左乘一个矩阵;相应的如果想对矩阵进行列变换,可以右乘一个矩阵。这种思想被应用到高斯消元的过程中。
最后我们总结一下矩阵C(C=AB)到底是什么,C是一个矩阵,是一个多面孔的矩阵。它既是列向量组成的行向量,每个列向量是A的列空间的线性组合,又是行向量组成的列向量,每个行向量是B的行空间的线性组合;它是一个内积,内积的每个成分是一个外积,同时它又是一个外积,外积矩阵的每一个元素是一个内积。
向量是由n个实数组成的一个n行1列(n*1)或一个1行n列(1*n)的有序数组;
向量的点乘,也叫向量的内积、数量积,对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个标量。
点乘公式
对于向量a和向量b:
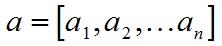
a和b的点积公式为:
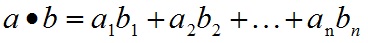
要求一维向量a和向量b的行列数相同。
点乘几何意义
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影,有公式:
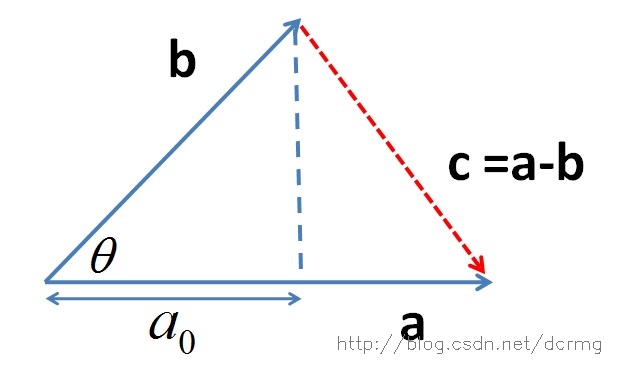
推导过程如下,首先看一下向量组成:
定义向量:
根据三角形余弦定理有:
根据关系c=a-b(a、b、c均为向量)有:
即:
向量a,b的长度都是可以计算的已知量,从而有a和b间的夹角θ:
根据这个公式就可以计算向量a和向量b之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:
a·b>0 方向基本相同,夹角在0°到90°之间
a·b=0 正交,相互垂直
a·b<0 方向基本相反,夹角在90°到180°之间
叉乘公式
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
对于向量a和向量b:
a和b的叉乘公式为:
其中:
根据i、j、k间关系,有:
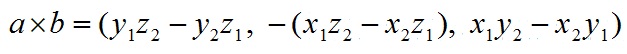
叉乘几何意义
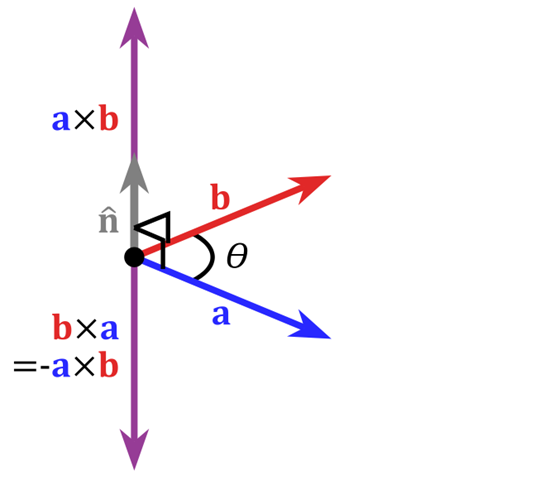
在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
在二维空间中,叉乘还有另外一个几何意义就是:aXb等于由向量a和向量b构成的平行四边形的面积。








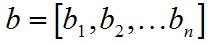
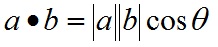
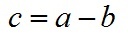
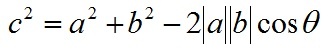
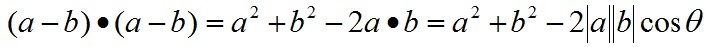
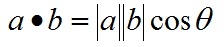
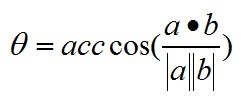
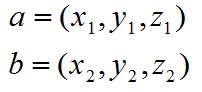
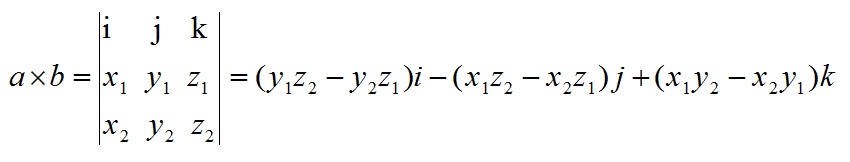
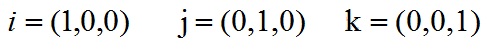
















 2399
2399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








