本文承接上一篇 约束优化方法之拉格朗日乘子法与KKT条件,将详解一些拉格朗日对偶的内容。都是一些在优化理论中比较简单的问题或者一些特例,复杂的没见过,但是简单的刚接触都感觉如洪水猛兽一般,所以当真是学海无涯。
在优化理论中,目标函数 f(x) 会有多种形式:如果目标函数和约束条件都为变量 x 的线性函数, 称该问题为线性规划; 如果目标函数为二次函数, 约束条件为线性函数, 称该最优化问题为二次规划; 如果目标函数或者约束条件均为非线性函数, 称该最优化问题为非线性规划。每个线性规划问题都有一个与之对应的对偶问题,对偶问题有非常良好的性质,以下列举几个:
- 对偶问题的对偶是原问题;
- 无论原始问题是否是凸的,对偶问题都是凸优化问题;
- 对偶问题可以给出原始问题一个下界;
- 当满足一定条件时,原始问题与对偶问题的解是完全等价的;
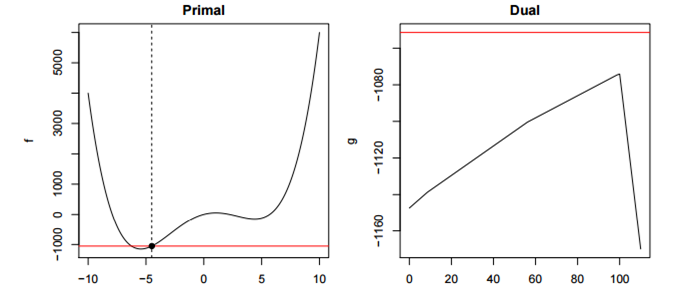
比如下边这个例子,虽然原始问题非凸,但是对偶问题是凸的:
原始问题
开始步入正题,首先给出不等式约束优化问题:
定义 Lagrangian 如下:
根据以上 Lagrangian 便可以得到一个重要结论:
(*) 式很容易验证,因为满足约束条件的 x 会使得 hi(x)=0 ,因此第二项消掉了;而 gj(x)≤0 ,并且使得 βj≥0 ,因此会有 βjgj(x)≤0 ,所以最大值只能在它们都取零的时候得到,这个时候就只剩下 f(x) 了。反之如果有任意一个约束条件不满足,则只需令其相应的乘子 →+∞ ,则会得到 L(x,α,β)→+∞ ,这样将导致问题无解,因此必须满足约束条件。经过这样一转变,约束都融合到了一起而得到如下的无约束的优化目标:
对偶问题
上式与原优化目标等价,将之称作原始问题 , 将原始问题的解记做 p∗ ,如此便把带约束问题转化为了无约束的原始问题,其实只是一个形式上的重写,方便找到其对应的对偶问题,首先为对偶问题定义一个对偶函数(dual function) :
有了对偶函数就可给出对偶问题了,与原始问题的形式非常类似,只是把 min 和 max 交换了一下:
然后定义对偶问题的最优解即关于 α β 的函数:
对偶问题和原始问题的最优解并不相等,而是满足的如下关系:
直观地,可以理解为最小的里最大的那个要比最大的中最小的那个要大。具体的证明过程如下:
证明在这里,首先这里的约束要全部满足,对偶问题与原始问题的关系如下:
D(α,β)=minxL(x,α,β)≤L(x,α,β)≤maxα,β,βi≥0L(x,α,β)=f(x)即 D(α,β)≤f(x) ,所以自然而然可得:
d∗=maxα,β;βi≥0D(α,β)≤minxf(x)=p∗即现在通过对偶性,为原始问题引入一个下界, d∗≤p∗ .
这个性质便叫做弱对偶性(weak duality),对于所有优化问题都成立,即使原始问题非凸。这里还有两个概念: f(x)–D(α,β) 叫做对偶间隔(duality gap), p∗–d∗ 叫做最优对偶间隔(optimal duality gap)。
之前提过无论原始问题是什么形式,对偶问题总是一个凸优化的问题,这样对于那些难以求解的原始问题 (甚至是 NP 问题),均可以通过转化为偶问题,通过优化这个对偶问题来得到原始问题的一个下界, 与弱对偶性相对应的有一个强对偶性(strong duality) ,强对偶即满足:
强对偶是一个非常好的性质,因为在强对偶成立的情况下,可以通过求解对偶问题来得到原始问题的解,在 SVM 中就是这样做的。当然并不是所有的对偶问题都满足强对偶性 ,在 SVM 中是直接假定了强对偶性的成立,其实只要满足一些条件,强对偶性是成立的,比如说 Slater 条件与KKT条件。
Slater 条件
若原始问题为凸优化问题,且存在严格满足约束条件的点 x ,这里的“严格”是指 gi(x)≤0 中的“ ≤ ”严格取到“ < ”,即存在 x 满足 gi(x)<0 , i=1,2,…,n ,则存在 x∗,α∗,β∗ 使得 x∗ 是原始问题的解, α∗,β∗ 是对偶问题的解,且满足:
p∗=d∗=L(x∗,α∗,β∗)
也就是说如果原始问题是凸优化问题并且满足 Slater 条件的话,那么强对偶性成立。需要注意的是,这里只是指出了强对偶成立的一种情况,并不是唯一的情况。例如,对于某些非凸优化的问题,强对偶也成立。SVM 中的原始问题 是一个凸优化问题(二次规划也属于凸优化问题),Slater 条件在 SVM 中指的是存在一个超平面可将数据分隔开,即数据是线性可分的。当数据不可分时,强对偶是不成立的,这个时候寻找分隔平面这个问题本身也就是没有意义了,所以对于不可分的情况预先加个 kernel 就可以了。
KKT条件
假设 x∗ 与 α∗,β∗ 分别是原始问题(并不一定是凸的)和对偶问题的最优解,且满足强对偶性,则相应的极值的关系满足:
这里第一个不等式成立是因为 x∗ 为 L(x,α∗,β∗) 的一个极大值点,最后一个不等式成立是因为 hi(x∗)=0 ,且 gj(x∗)≤0,βj≥0 ,( βj≥0 是之前 (*) 式的约束条件)因此这一系列的式子里的不等号全部都可以换成等号。根据公式还可以得到两个结论:
1)第一个不等式成立是因为 x∗ 为 L(x,α∗,β∗) 的一个极大值点,由此可得:
2)第二个不等式其实就是之前的 (*) 式, β∗jgj(x∗) 都是非正的,所以这里有:
也就是说如果 β∗j>0 ,那么必定有 gj(x∗)=0 ;反过来,如果 gj(x∗)<0 那么可以得到 β∗j=0 ,即:
这些条件都似曾相识,把它们写到一起,哎?不就是传说中的 KKT (Karush-Kuhn-Tucker) 条件么:
∇xL(x,α,β)βjgj(x)hi(x)gj(x)βj=0=0, j=1,2,...,n=0, i=1,2,...,m≤0, j=1,2,...,n≥0, j=1,2,...,n(1)(2)(3)(4)(5)
总结来说就是说任何满足强对偶性的优化问题,只要其目标函数与约束函数可微,任一对原始问题与对偶问题的解都是满足 KKT 条件的。即满足强对偶性的优化问题中,若 x∗ 为原始问题的最优解, α∗,β∗ 为对偶问题的最优解,则可得 x∗,α∗,β∗ 满足 KKT 条件。不知道够不够清楚,书中原话(P243)是这样的 7.1 :
上面只是说明了必要性,当满足原始问题为凸优化问题时,必要性也是满足的,也就是说当原始问题是凸优化问题,且存在 x∗,α∗,β∗ 满足 KKT 条件,那么它们分别是原始问题和对偶问题的极值点并且强对偶性成立,证明如下:
首先原始问题是凸优化问题,固定 α∗,β∗ 之后对偶问题 D(α∗,β∗) 也是一个凸优化问题, x∗ 是 L(x,α∗,β∗) 的极值点:
最后一个式子是根据 KKT 条件中的 hi(x)=0 与 βjgj(x)=0 得到的。这样一来,就证明了对偶间隔为零,也就是说,强对偶成立。 所以当原始问题为凸优化问题时,书中的原话(P244)如下 7.1 :
关于对偶的问题到此为止,其实都是很优化方法中比较简单的内容。总结一下。本文介绍了对偶的基本概念,对于一个约束优化问题,找到其对偶问题,当弱对偶成立时,可以得到原始问题的一个下界。而如果强对偶成立,则可以直接求解对偶问题来解决原始问题。 SVM 就是这样的。对偶问题由于性质良好一般比原始问题更容易求解,在 SVM 中通过引入对偶问题可以将问题表示成数据的内积形式从而使得 kernel trick 的应用更加自然)。此外,还有一些情况会同时求解对偶问题与原始问题 ,比如在迭代求解的过程中,通过判断对偶间隔的大小,可以得出一个有效的迭代停止条件。









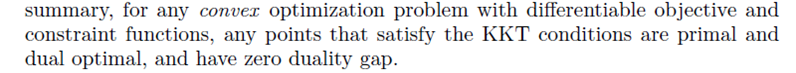













 8043
8043











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








