线段树（原理，模板）

线段树

线段树是用来维护 区间信息 的数据结构

它可以在 $O(\log n)$ 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

信息是否可以由线段树来维护，要看一段区间的信息，是否可以由它的子区间推导而来，显然加法，求最值都是满足这种性质的。从离散数学的角度来说，可以认为是满足幺半群性质的信息。对于有些复杂的题目，单一的信息可能并不能满足这一性质，而需要多个信息共同维护才能满足。

线段树的形态：

将一段区间看做一个结点，长度为 10 的数组可以生成如下线段树。

父结点表示整个区间，将其划分为左右两个区间作为孩子，不断递归划分，直到区间长度为 1。

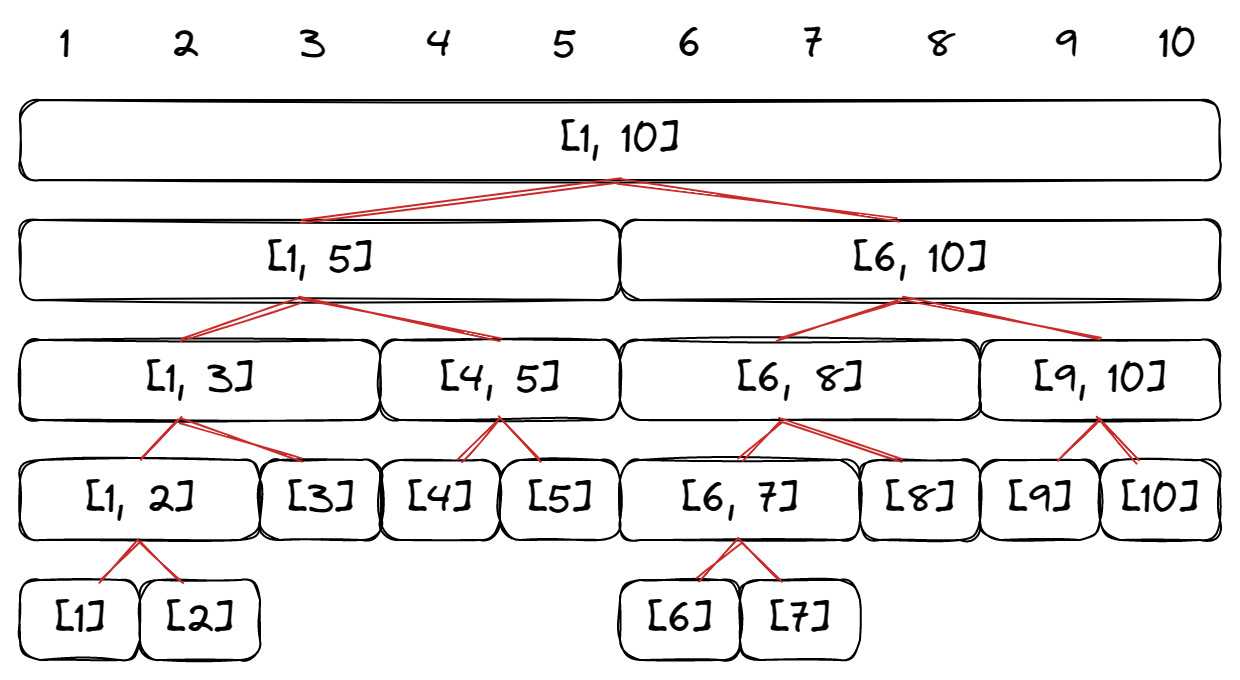
可以看到，线段树接近于一棵满二叉树，所以可以像堆一样，用一维数组来存储（即，若某一结点下标为 u，则其父结点下标为 u / 2，左孩子下标为 2 * u，右孩子下标为 2 * u + 1）。

一个长度为 $n$ 的数组，所建立的线段树，倒数第二层接近有 $n$ 个结点，将其以上看作满二叉树，则二叉树的高度为 ${\log }_{2}n+1$ ，共有 $2^{{\log }_{2}n+1}-1$ 个结点，化简得 $2n-1$，最后一层最坏情况是倒数第二层的两倍，看作有 $2n$ 个点，所以估计最坏情况有 $4n-1$ 个点，所以我们开大小为 $4n$ 的数组。

---

• 线段树一共有 5 个操作：
  • pushup 用子节点的信息来更新父结点
  • pushdown 向下分配懒惰标记（用于区间修改）
  • build 初始化线段树
  • query 查询
  • modify 修改

pushup 需要根据自己维护的区间信息来编写：如维护区间最大值，则父结点的区间最大值就是max(左孩子区间最大值, 右孩子区间最大值)；如维护区间和，父结点区间和 = 左孩子区间和 + 右孩子区间和。

build 递归建树，基本模板：

注意左右子树初始化完成后需要 pushup 当前结点。

void build(int u, int l, int r) {
    tr[u] = {l, r};
    if (l == r) return;
    int mid = (l + r) / 2;
    build(2 * u, l, mid);
    build(2 * u + 1, mid + 1, r);
    pushup(u);
}

query 查询区间

如图，如果我们要查询 $[5,9]$ 的信息，则最终需要 $[5],[6,8],[9]$ 三个区间合并求得。（阴影标注的是递归需要经过的结点）

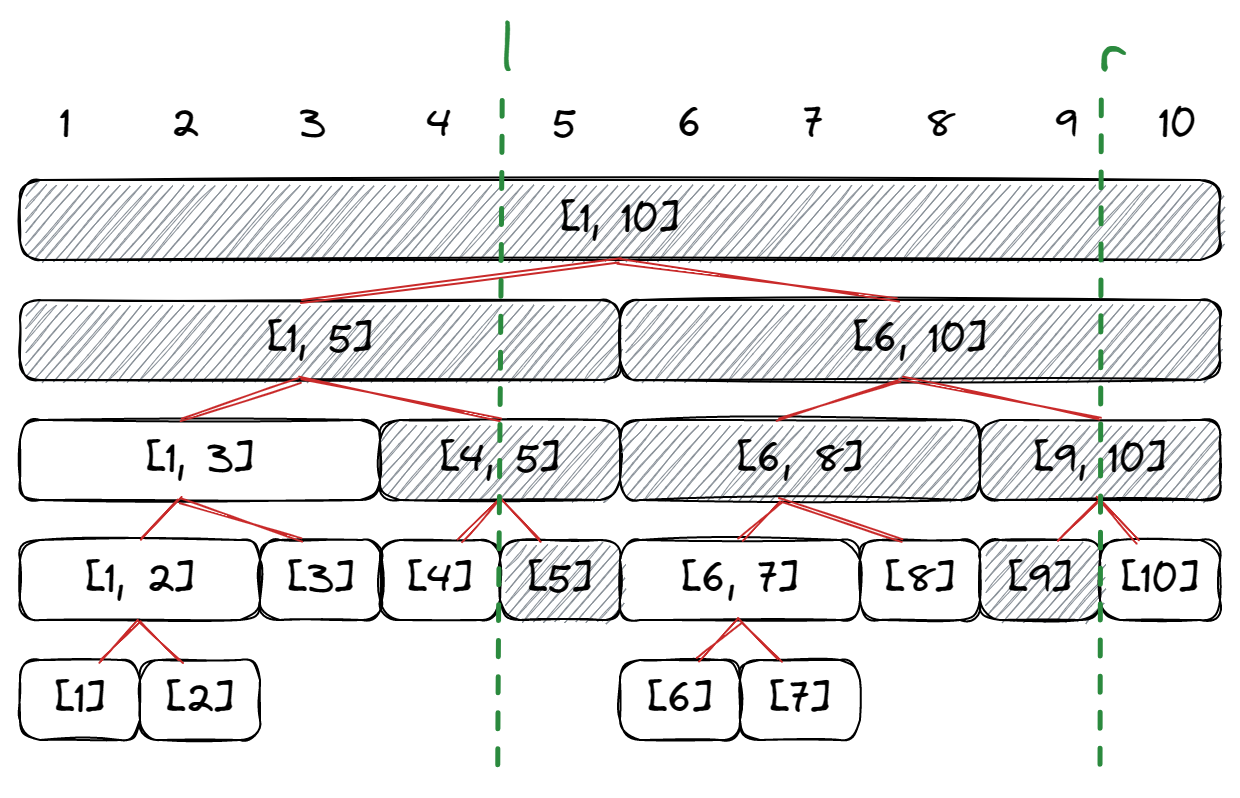
我们从根结点开始查询，要查询的区间和当前结点的孩子有下面三种情况：

• 只跟左孩子有交集：则继续递归左孩子，不递归右孩子
• 只跟右孩子有交集：则继续递归右孩子，不递归左孩子
• 跟两个孩子都有交集：继续递归左右两个孩子

如果当前结点的区间完全在要查询的区间的内部，则直接返回当前结点的信息。

注意：不存在和两个孩子都没有交集的情况，因为如果和两个孩子都没有交集，则意味着和当前结点也没有交集，而要查询的区间一定和根结点有交集，递归只会向下找其和要查询的区间有交集的孩子，所以当前结点不可能和要查询的区间没有交集。

modify ：单点修改只需要递归向下搜索，同时使用 pushup 回溯即可。

线段树代码(单点修改、区间查询)

一个基本的线段树有 4 个操作，可以支持区间查询和单点修改

以维护 区间最大值 为例，有如下代码：

• tr[i]：编号为 i 的结点表示的区间为 [l, r]，值为 v，根结点编号为 1
• build：从上至下初始化线段树各个结点的区间，每个区间的值我们没有更新，因为这里默认原数组元素全为 0。
• query：查询 [l，r] 区间，如果当前结点的区间包含在 [l，r] 里面，那么直接返回值即可，否则递归左右结点中和 [l，r] 有交集的区间。返回查询结果（max）。
• modify：单点修改，将下标 x 位置修改为 v。先递归搜索 x 所在的区间，找到叶子结点直接修改即可，回溯的时候调用 pushup 函数来用子结点更新父结点。

const int N = 100010;

struct Node {
    int l, r;
    int v;
}tr[4 * N];

void pushup(int u) {
    tr[u].v = max(tr[2 * u].v, tr[2 * u + 1].v);
}

void build(int u, int l, int r) {
    tr[u] = {l, r};
    if (l == r) return;
    int mid = (l + r) / 2;
    build(2 * u, l, mid);
    build(2 * u + 1, mid + 1, r);
}

int query(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].v;
    int mid = (tr[u].l + tr[u].r) / 2;
    int v = 0;
    if (l <= mid) v = query(2 * u, l, r);
    if (r > mid) v = max(v, query(2 * u + 1, l, r));
    return v;
}

void modify(int u, int x, int v) {
    if (tr[u].l == x && tr[u].r == x) tr[u].v = v;
    else {
        int mid = (tr[u].l + tr[u].r) / 2;
        if (x <= mid) modify(2 * u, x, v);
        else modify(2 * u + 1, x, v);
        pushup(u);
    }
}

懒惰标记与区间修改

懒惰标记可以通过延迟对结点的修改，减少操作次数。

当我们要执行修改时，可以使用 modify 将当前结点的信息进行更新，但不再向下递归，而是给当前结点打上懒惰标记，该标记表示，当前结点以下的所有子节点（不包括当前结点）都需要更新。当下一次访问到带有标记的结点的孩子之前，才对结点的孩子进行实质性的修改。在这样的设定下，根结点和当前结点的信息一定是最新的（正确的）。当然也可以让懒惰标记包括当前结点，这里所给出的是前一种代码。

以维护 区间和 为例，我们的懒惰标记就设置为 add，它是一个整型，表示该结点所表示的区间的每个元素都要加 add，其下的所有子节点都需要更新。

• pushdown 用来下放懒惰标记，就是将当前结点的懒惰标记叠加到左右孩子的懒惰标记上，清空当前结点的懒惰标记，并对左右孩子进行实质性修改。

• modify：将 [l, r] 区间的元素加上 d。

  • 如果当前区间在 [l, r] 区间内部，则直接修改当前区间，并打上懒惰标记，不向下递归。
  • 否则，因为即将访问到需要进行实质性修改的子结点，所以需要先将当前结点的懒惰标记下放。否则就会导致 pushup 使用错误的子结点的信息来更新当前结点。

总结：每次（modify、query）递归子结点之前都要 pushdown，所有修改操作（build、modify）递归完子结点之后都要 pushup

const int N = 100010;

int w[N]; // 原数组
struct Node {
    int l, r;
    int sum, add;
}tr[4 * N];

void pushup(int u) {
    tr[u].sum = tr[2 * u].sum + tr[2 * u + 1].sum;
}

void pushdown(int u) {
    Node& root = tr[u], &left = tr[2 * u], &right = tr[2 * u + 1];
    if (root.add) {
        left.add += root.add;
        right.add += root.add;
        left.sum += (left.r - left.l + 1) * root.add;
        right.sum += (right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}

void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, w[l], 0};
    else {
        tr[u] = {l, r};
        int mid = (l + r) / 2;
        build(2 * u, l, mid);
        build(2 * u + 1, mid + 1, r);
        pushup(u);
    }
}

void modify(int u, int l, int r, int d) {
    if (l <= tr[u].l && tr[u].r <= r) {
        tr[u].sum += (tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
    } else {
        pushdown(u);
        int mid = (tr[u].l + tr[u].r) / 2;
        if (l <= mid) modify(2 * u, l, r, d);
        if (r > mid) modify(2 * u + 1, l, r, d);
        pushup(u);
    }
}

int query(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
    pushdown(u);
    int mid = (tr[u].l + tr[u].r) / 2;
    int sum = 0;
    if (l <= mid) sum += query(2 * u, l, r);
    if (r > mid) sum += query(2 * u + 1, l, r);
    return sum;
}

树状数组与区间修改

上一节 树状数组（代码模板和原理详解）_世真的博客-CSDN博客 讲到，树状数组只支持单点修改和区间查询，不支持区间修改。

但是如果题目让我们对一个数组进行区间修改和求区间和，其实也可以使用树状数组。不同于线段树的是，线段树可以直接维护这个数组，而树状数组需要维护它的差分数组。

对差分数组的单点修改等价于对原数组的区间修改。

但是这又带来一个问题：对差分数组的区间求和，相当于求原数组的单点值，而我们要的是对原数组的区间求和，这怎么解决呢？

设原数组 $a$ 内的一个前缀区间的元素为 $a_1,a_2,\cdots ,a_x$，其对应的差分为 $b_1,b_2,\cdots ,b_x$

则
$$\sum _{i=1}^x{a}_i=\sum _{i=1}^x\sum _{j=1}^i{b}_j$$
把各项列出来（黑色部分）：

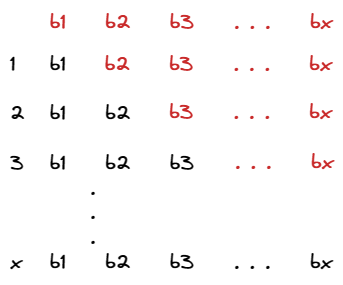
将三角补全成一个完整的矩阵（红色部分）

黑色部分等于整个矩阵的和减去红色部分
$$(b_1+b_2+b_3+\cdots +b_x)\times (x+1)-(b_1+2b_2+3b_3+\cdots +x{b}_x)$$
这个式子就是用 $b_i$ 的前缀和，乘 $x+1$ 后减去 $i{b}_i$ 的前缀和。

所以我们需要维护两个数组，分别是差分数组 $b_i$ 和 $i{b}_i$ 数组。

代码如下：

const int N = 100010;

int n, m;
int a[N];
int tr1[N];
int tr2[N];

int lowbit(int x) {
    return x & -x;
}

void add(int tr[], int x, int c) {
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

int sum(int tr[], int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int prefix_sum(int x) {
    return sum(tr1, x) * (x + 1) - sum(tr2, x);
}

int range_sum(int l, int r) {
    return prefix_sum(r) - prefix_sum(l - 1);
}

void range_add(int l, int r, int c) {
    add(tr1, l, c);
    add(tr1, r + 1, -c);
    add(tr2, l, l * c);
    add(tr2, r + 1, (r + 1) * -c);
}