点到三角形的最近点--二次规划

最新推荐文章于 2023-03-25 18:02:37 发布
最新推荐文章于 2023-03-25 18:02:37 发布
阅读量774 收藏 1
点赞数 1
分类专栏： 数学 文章标签： 二次规划 几何最优化 有效集
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/hongmaodaxia/article/details/103945452
版权

文章目录

问题如下在三角形中找一个点p到三角形内部最近的点（可能在边上，顶点上或者内部）
在这里插入图片描述
这个当然可以用几何的方法用条件判断，这里介绍建模为优化问题

其实这个问题可以表示为
a r g m i n x ∥ A x − p ∥ 2 2 , s . t . ∑ x = 1 , x > = 0 arg min _x \| Ax - p \|_2^2, \quad s.t. \sum_x=1, x>=0 argminx​∥Ax−p∥22​,s.t.x∑​=1,x>=0
就是三角形内部的点可以用顶点差值表示(重心坐标)，这样就转换成了最小二乘问题。

有趣的是其实这个问题的弱化版为 找线段外一点到这个线段最近的位置。我就是通过这个简单的例子最终发现单纯型法算不出来。

求解这个其实可以经过一些推导转化成类似线性规划的问题，但是有个ux=0的情况，表示如果用单纯性算法时，互补松弛变量不能同时作为基变量 （推了很长时间就是无法实现）。

后面展示了用库求解和用有效集的方法求解

1. 用二次规划的库求解

def problem(tri_p, px):
    At = tri_p
    A = At.T
    Atb = At.dot(px)
    AtA = At.dot(A)
    return AtA, Atb

from cvxopt  import solvers, matrix 
tri_p=np.array([
    [0, 0], [2, 0], [1, 2]
], np.float64)
px = np.array([1, 3], np.float64)

# 似乎必须是 float64
P, q = problem(tri_p, px)
P = matrix(P)
q = matrix(-q)
G = matrix(-np.eye(3))
h = matrix(np.zeros(3))
A = matrix(np.ones((1, 3)))
b = matrix(np.array([1.]))

sol = solvers.qp(P,q,G,h,A,b)

#print(sol)
print(sol['x'])

输出如下
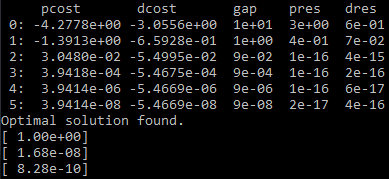
在这里插入图片描述

2.（失败） 尝试的单纯型法

这个就不要看了，主要是推导了很长时间，换了很多种方法都没有弄出来。
大体思路就是KKT条件后，构造等式约束，并构造一个目标函数。最后发现达不到最优点

def f5(tri_p, px):
    _A, _b = problem(tri_p, px)
    neg  = _b<0
    if neg.sum()>0:
        _A[neg] *= -1
        _b[neg] *= -1
        
    nall = 3+3+4+2
    A=np.zeros( (4, nall) )
    b=np.zeros( (4) )
    
    A[:3, :3] = _A
    A[:3, 3:3+3] = -np.eye(3)
    
    A[3, :3] = 1
    
    A[:3, 10] = -1
    A[:3, 11] = 1
    A[:4, 6:10] = np.eye(4)
    
    b[:3] = _b
    b[3] = 1
    
    enters = np.arange(6, 10)
    
    slack = np.arange(nall)
    
    slack[:3], slack[3:3+3] = slack[3:3+3].copy(), slack[:3].copy()
    slack[10:12] = 9
    
    z = np.zeros( nall + 1 )
    
    arg_type="max"
    #z[nall-4:-1] = -1
    z[6:10] = -1
    #z[nall-5:-1] = -1
    #z[nall-6] = 1
    
    # p(enters)
    # p(slack)
    # p(A)
    # p(z)
    
    for i in range(4):
        change_A_b(A, b, z, i, enters[i])
    
    # p(A)
    # p(b)
    # p(z)
    # exit()
    f5_solve(A, b, z, enters, (slack), arg_type, n_it=20)
    x = np.zeros( nall )
    x[enters] = b
    p("mx", x)
    return x[:3]


def f5_solve(A, b, z, enters, slack, arg_type, n_it=20):
    for i in  range(n_it):
        if not sel_enter_outer(A, b, z, enters, arg_type, slack): break
        

def sel_enter_outer(A, b, z, enters, arg_type="max", slack=None):
    r, c = A.shape
    slack_mp = None
    if len(slack)==2:
        slack, slack_mp = slack
    vc = np.zeros(c)
    for _c in range(c):
        ci = sel_enter_idx(z[:-1], arg_type, enters, vc)
        if ci < 0: return False
        vc[ci] = 1
        ri = sel_outer_idx(A[:, ci], b)
        if ri < 0: continue
        #p("ci, ri", ci, enters[ri])
        if slack is None: break
        else:
            if slack[ci]==enters[ri] or slack[ci] not in enters: 
                if slack_mp and ci in slack_mp:
                    if slack[ci]==enters[ri]:
                        if slack_mp[ci] not in enters: break
                        else: continue
                    else:
                        if slack_mp[ci]==enters[ri] or slack_mp[ci] not in enters: break
                else: break
    if _c==c: return False
    p("ci, ri, z", ci, enters[ri], z)
    change_A_b(A, b, z, ri, ci)
    enters[ri] = ci
    p("ck---")
    p(enters)
    #p(A)
    #p(b)
    p(z)
    
    return True

def change_A_b(A, b, z, ri, ci):
    b[ri] /= A[ri, ci]
    A[ri] /= A[ri, ci].copy()
    for i in range(len(b)):
        if i!=ri:
            b[i] -= A[i, ci]*b[ri]
            A[i] -= A[i, ci]*A[ri]
    z[-1] -= z[ci]*b[ri]
    z[:-1] -= z[ci]*A[ri]
    
    
# 0 是可以找的    
def sel_enter_idx(z, arg_type, enters, vc):
    if arg_type=="max": mm = -1
    elif arg_type=="min": mm = 1
    _i = -1
    for i in range(len(z)):
        if vc[i]: continue # 不合法的直接不要
        if i in enters: continue
        if arg_type=="max":
            if z[i]<=0: continue
            if mm < z[i]:
                mm = z[i]
                _i = i
        else:
            if z[i]>=0: continue
            if mm > z[i]:
                mm = z[i]
                _i = i
    return _i
    
def sel_outer_idx(a_c, b):
    mx=np.inf
    _i = -1
    for i in range(len(b)):
        if a_c[i]>0 and mx > (b[i]/a_c[i]):
            mx=b[i]/a_c[i]
            _i = i
    return _i

3. 有效集法 【本次最值得记录的】

https://wenku.baidu.com/view/ad34f36079563c1ec5da71fc.html
其实之前感觉弄不出来的时候就想到找了，一开始感觉很复杂，所以不想看。后面仔细看了一下，感觉也很好了解。
整体思路就类似，高斯牛顿法，给个初始值，然后求dp，但是这里主要多了个保证在可行域之中。

里面应该求解那里有重复计算的地方，这里就不优化了。

def f7(tri_p, px):
    A, b = problem(tri_p, px)
    n_x = 3
    n_eq = 1
    n_neq = n_x
    n_max_Q = n_x + n_eq + n_neq # 2 个变量， 1个等式变量，最多2个不等式变量
    valid = np.zeros(n_max_Q, np.bool)
    Q = np.zeros( (n_max_Q, n_max_Q) )
    Ae = np.zeros( (n_eq, n_x) ) + 1 # task 有关
    be = np.zeros( (n_eq) ) + 1
    #Ane = np.zeros( (n_neq, n_x) )
    Ane = np.eye( n_x )
    bne = np.zeros( (n_neq) )
    
    Q[:n_x, :n_x] = A
    Q[:n_x, n_x:n_x+n_eq] = -Ae.T
    Q[n_x:n_x+n_eq, :n_x] = Ae
    Q[:n_x, n_x+n_eq:] = -Ane.T
    Q[n_x+n_eq:, :n_x] = Ane
    
    q = np.zeros( n_max_Q )
    q[:n_x] = b
    q[n_x:n_x+n_eq] = be
    q[n_x+n_eq:] = bne
    
    # p(Q)
    # p(q)
    # exit()
    
    valid[:n_x+n_eq] = True
    
    n_must = n_x+n_eq
    # task 有关
    x_init=np.zeros(n_x) + 1/n_x
    oA, ob = A, b
    
    #q[n_x:] = 0 # 才发现根本没有用
    bi = n_x + n_eq
    _cnt=0
    while True:
        p("x:", x_init)
        d_f_x_k = oA.dot(x_init) - ob
        q[:n_x] = -d_f_x_k # 修改了初始值，则重新构造求解 dx 的 b
        
        A = Q[valid][:, valid]
        b = q[valid].copy()
        b[n_x:] = 0
        
        # 有重复计算
        AtA = A.T.dot(A)
        Atb = A.T.dot(b)
        
        d = np.linalg.solve(AtA, Atb)
        #_cnt+=1
        #if _cnt>10: exit()
        p(_cnt, np.abs(d[:n_x]).sum())
        # 达到极值
        if np.abs(d[:n_x]).sum() < 1e-6:
            if d.shape[0] == bi: break # 所有等式不等式都满足了，
            mm = np.min(d[bi:])
            if mm>=0: break
            # 把最不能满足不等式约束的去掉
            valid[bi:][valid[bi:]][np.argmin(d[bi:])] = False
            
        else:
            # 不为0，基本就说明约束不够， 达不到极值
            # step 1：保证安求出的下降方向更新后，未参与的约束合法
            alpha = 1
            # 【只针对不等式约束】
            for i in range(bi, bi+n_neq):
                if not valid[i]:
                    # 对于不在可行解之中的
                    fm = Q[i, :n_x].dot(d[:n_x])
                    if fm<0: # 可能会出了可行域， 因为不等式是 >= b， 所以如果fm小于0则可能 出现<b
                        # a^T(x+\alpah d) = b -> \alpha = (b-a^Tx)/
                        alpha = min(alpha, (q[i]-Q[i, :n_x].dot(x_init))/fm)
                        assert alpha!=0

            x_init += alpha*d[:n_x] # 更新当前解
            
            # step2: 发现有新的有效约束则加入，也是不等式中
            for i in range(bi, bi+n_neq):
                if not valid[i]:
                    if np.abs(q[i]-Q[i, :n_x].dot(x_init))<1e-9:
                        valid[i] = True
            
            #p("alpha", alpha, d)
            
    p(x_init) 
    return x_init

4. 调试时的其他代码

4.1 杂记

def plot_triangle(A, B, C):
    x = [A[0], B[0], C[0], A[0]]
    y = [A[1], B[1], C[1], A[1]]
    plt.plot(x, y, linewidth=2)

def f_cmp(tri_p, px, x1, x2):
    r1 = _cac(tri_p, px, x1)
    r2 = _cac(tri_p, px, x2)
    p(r1, r2)
    abs = np.abs( r1 - r2 ).sum()
    return abs<1e-6

def plot_line(A, B):
    x = [A[0], B[0]]
    y = [A[1], B[1]]
    plt.plot(x, y, linewidth=2)

4.2 关于线段和点的

在这里插入图片描述

plt.gca().set_aspect('equal', adjustable='box')
plot_line(tri_p[0], tri_p[1])
plt.plot( px[0], px[1], "r." )
plt.plot( tri_p[0][0], tri_p[0][1], "g*" )
plt.plot( tri_p[1][0], tri_p[1][1], "y+" )
p1 = tri_p.T.dot(x1)
p2 = tri_p.T.dot(x2)
plt.plot( p1[0], p1[1], "b*" )
plt.plot( p2[0], p2[1], "r*" )
plt.show()

# 可以解析求解, 利用余弦函数的。 x = |p21||px1|cos / |p21|^2
def f6(tri_p, px):
    p1 = tri_p[0]
    p2 = tri_p[1]
    p21 = p2 - p1
    px1 = px - p1
    x = (p21*px1).sum()/(p21*p21).sum()
    if x<0: x=0
    if x>1: x=1
    return np.array([1-x, x])

# 也可以用有效集的方法
def f7(tri_p, px):
    A, b = problem(tri_p, px)  # AtA, Atb
    n_x = 2 # 未知数变量
    n_eq = 1 # 1 等式 
    n_neq = n_x
    n_max_Q = n_x + n_eq + n_neq # 2 个变量， 1个等式变量，最多2个不等式变量
    valid = np.zeros(n_max_Q, np.bool)
    Q = np.zeros( (n_max_Q, n_max_Q) )
    Ae = np.zeros( (n_eq, n_x) ) + 1 # task 有关
    be = np.zeros( (n_eq) ) + 1
    #Ane = np.zeros( (n_neq, n_x) )
    Ane = np.eye( n_x ) 
    bne = np.zeros( (n_neq) )
    
    Q[:n_x, :n_x] = A
    Q[:n_x, n_x:n_x+n_eq] = -Ae.T
    Q[n_x:n_x+n_eq, :n_x] = Ae
    Q[:n_x, n_x+n_eq:] = -Ane.T
    Q[n_x+n_eq:, :n_x] = Ane
    
    q = np.zeros( n_max_Q )
    q[:n_x] = b
    q[n_x:n_x+n_eq] = be
    q[n_x+n_eq:] = bne
    
    # p(Q)
    # p(q)
    # exit()
    
    # 上面的Q，q是使用所有的等式，通过valid决定具体用哪个？
    valid[:n_x+n_eq] = True
    
    n_must = n_x+n_eq
    # task 有关
    x_init=np.zeros(n_x) + 1/n_x
    oA, ob = A, b
    
    #q[n_x:] = 0 # 才发现根本没有用
    bi = n_x + n_eq
    _cnt=0
    while True:
        p("x:", x_init)
        d_f_x_k = oA.dot(x_init) - ob
        q[:n_x] = -d_f_x_k
        
        A = Q[valid][:, valid]
        b = q[valid].copy()
        b[n_x:] = 0
        
        # 有重复计算
        AtA = A.T.dot(A)
        Atb = A.T.dot(b)
        
        d = np.linalg.solve(AtA, Atb)
        #_cnt+=1
        #if _cnt>10: exit()
        p(_cnt, np.abs(d[:n_x]).sum())
        if np.abs(d[:n_x]).sum() < 1e-6:
            if d.shape[0] == bi: break
            mm = np.min(d[bi:])
            if mm>=0: break
            # 把最不能满足不等式约束的去掉
            valid[bi:][valid[bi:]][np.argmin(d[bi:])] = False
            # cnt=0
            # mm = 0
            # sel = None
            # for i in range(bi, bi+n_neq):
                # if valid[i]:
                    # if d[bi+cnt]<mm: 
                        # mm = d[bi+cnt]
                        # sel = i
                    # cnt+=1
            # if mm == 0: break
            # valid[i] = False # 最小的那个去掉
        else:
            # step 1：保证更新之后，未参与的约束合法
            alpha = 1
            for i in range(bi, bi+n_neq):
                if not valid[i]:
                    # 对于不在可行解之中的
                    fm = Q[i, :n_x].dot(d[:n_x])
                    if fm<0: # 可能会出了可行域， 因为不等式是 >= b， 所以如果fm小于0则可能 出现<b
                        # a^T(x+\alpah d) = b -> \alpha = (b-a^Tx)/
                        alpha = min(alpha, (q[i]-Q[i, :n_x].dot(x_init))/fm)
                        assert alpha!=0

            x_init += alpha*d[:n_x]
            
            # step2: 发现有新的有效约束则加入
            for i in range(bi, bi+n_neq):
                if not valid[i]:
                    if np.abs(q[i]-Q[i, :n_x].dot(x_init))<1e-9:
                        valid[i] = True
            
            #p("alpha", alpha, d)
            
    p(x_init) 
    return x_init
长虹剑
关注
  • 1
    点赞
  • 踩
  • 1
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
专栏目录
点至三角形的最近点
折戟
07-13 1027
文章目录已优化版本未优化版本 点P到三角形的相交点分为三种情况： 1.顶点域，相交点为三角形的三个顶点 2.边域，相交点在三角形的三条边上，也就是点P在边上的投影 3.中心域，相交点在三角形内部，也就是点P在三角形中的投影 代码如下： 已优化版本 /// <summary> /// 点到三角形最近点,已优化cross为dot /// 求解思路：平面的法线和pa，pb，pc的法线进行dot，可知p是落在哪个域上，再对p在各个边上进行投影，求得边域上最近点。在三角形内就是质心
点到某三角形的最短距离
qq_23523219的博客
07-20 980
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题，有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注脚注释也是必不可少的KaTeX数学公式新的甘特图功能，丰富你的文章UML 图表FLowchart流程图导出与导入导出导入 欢迎使用Markdown编辑器 你好！ 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Mar
计算三维空间中点到三角形平面的最短距离
llduncan的博客
11-26 6819
在R3空间，点p到平面（n,d）的距离很简单，就是double dist = p*n+d,当然这个是有向距离，投影点当然就是p-n*dist。这个简单的计算好像至今也没有一个来面试的人告诉我过我这么简洁的答案。希望下次告诉我这个答案的人能给我讲清楚个中原理哦。 那现在约束一下，在R3中求点p到三角形T{ABC}的最短距离？ 如下图，不过有个问号，谁能解释下？
计算几何---点与三角形面片的关系
weixin_30770495的博客
08-02 510
点是否再三角形面之内的位置关系判定 　　常用的方法是，如果点在三角形内部，则连接与三角形的三个顶点，并计算组成的组成矢量的角度和，如果为2pei， 则在三角形内部，否则不再三角形内不。理论上该方法可行，但是效率非常慢。 　　因为要计算夹角，需要多次计算平方根。 1. 判定是否同边的技术原理（Same Side Technique） 　　快速且简洁的方法如下： 　　　 　　如图，三角形，...
中科大-凸优化 笔记（lec26）-二次规划
scu-liu的博客
02-13 1366
全部笔记的汇总贴（视频也有传送门）：中科大-凸优化 一、二次规划（Quadratic Programming） min⁡12XTPX+ξTx+r      （凸）P∈S+ns.t.      Qx≤h  Ax=b（仿射）\min \frac12X^TPX+\xi^Tx+r\;\;\;（凸）P\in S_+^n\\s.t.\;\;\;Qx\le h\;Ax=b（仿射）min21​XTPX+ξTx+r（凸）P∈S+n​s.t.Qx≤hAx=b（仿射） 二、二次约束二次规划（Quadratizally cons
二次函数练习四往年数学知识点.doc
10-14
以上是对题目中所涉及的二次函数知识点的详细解释和解答，这些知识点包括二次函数的性质、解不等式、求二次函数解析式、求三角形面积以及利用二次函数解决实际问题的方法。理解并掌握这些内容对于学习和应用二次函数...
js代码-leetcode120 三角形最小值动态规划
07-15
在LeetCode的第120题“三角形最小路径和”中，我们面临的挑战是找到一个二维数组（三角形）中的最短路径，路径上的数字之和最小。这是一个典型的动态规划问题，我们可以用JavaScript来解决。本文将深入探讨这个问题...
判断一点是否在三角形内
05-08
2. **射线法**：从点P向无穷远画一条射线，如果射线与三角形的边相交的次数为奇数次，那么点P在三角形内。此方法适用于不包括边界的情况，若需考虑边界，需进行额外处理。 接下来，我们使用C++和OpenCV实现这个功能...
第三节--动点--二次函数与等腰三角形存在性问题.docx
10-11
在这些题目中，我们主要探讨的是如何在二次函数背景下解决动点问题，特别是涉及等腰三角形的存在性问题。这些问题通常需要对二次函数的性质、等腰三角形的定义以及几何图形的性质有深入理解。 1. **二次函数解析式*...
解直角三角形-教学反思1-4.doc
10-11
解直角三角形是初中数学几何部分的重要知识点，它涉及到直角三角形的性质和应用。在教学过程中，教师需要深入理解和掌握解直角三角形的基本方法，包括利用勾股定理和三角函数来求解直角三角形的未知元素。然而，教学...
几何算法面试准备（1）
最新发布
qq_40690772的博客
03-25 586
齐次坐标能做什么？它是怎么去区分是一个位置，还是一个方向？为什么使用齐次坐标，它有什么好处？原因：在欧氏几何空间，同一平面的两条平行线不能相交。然而，在透视空间里面，两条平行线可以相交。笛卡尔坐标系下（1，2）的齐次坐标可以表示为（1，2，1），如果点（1，2）移动到无限远处，在笛卡尔坐标下它变为(∞,∞)，然后它的齐次坐标表示为（1，2，0），因为(1/0, 2/0) = (∞,∞)，为什么叫齐次坐标？我们把齐次坐标转化为笛卡尔坐标的方法是前面n-1个坐标分量分别除以最后一个分量即可。
有效集法介绍（Active Set Method）
青梅煮酒
10-29 8187
单纯性法（Simplex Method）是“线性规划之父”George Dantzig 最著名的成果，也是求解线性规划最有力的算法之一。而这一算法在求解二次规划（Quadratic Programming, QP）时的升级版就是有效集法（Active Set Method, ASM）。这两种算法的特点都是迭代点会循着约束边界前进，直到达到问题的最优点。本文对用于求解 QP 命题的 Primal A...
不等式约束二次规划——有效集法
w_w_y的博客
05-09 6178
不等式约束二次规划——有效集法
点到平面（三角形）的最短距离
Nhsoft的专栏
07-24 9643
<br />有时候，我们经常需要计算一个点P到平面上的投影（P')，简单的讲，这个投影点P'能满足|P-P'|为P到平面的最短距离。<br />简单介绍一下如何计算该算法<br />假设平面以三点式给出，三个顶点分别为p0,p1,p2<br /> <br />那么以P0为原点， v0 = P1-P0 , v1 = P2-P0.<br />[v0 , v1] 为该平面的一个基， 注意不是正交的。<br /> <br />所以平面上的任意一点为  Pt = P0 + t0 * v0 + t1 * v1;<br
点到三角形的距离（三维）-使用Geometric Tools库
dhj555的博客
06-26 4747
在处理三维网格的时候，会遇到使用点到点距离、点到面距离、面到面距离（只讨论欧氏距离）等信息。点到点的距离很好计算，后面两者计算就很麻烦。最近在网上找到了一个很强大的几何图形处理库，利用其可以很方便的计算点到三角形的距离。点到三角形距离文档：https://www.geometrictools.com/Documentation/DistancePoint3Triangle3.pdf该pdf详细讲解...
点到三角形（二维平面）的距离 算法笔试ｐｙｔｈｏｎ
wuxulong123的博客
04-11 2134
不确定理解的对不对，仅供参考 点可能在三角形内，也可能在三角形外，点在三角形内则返回0；在三角形外则返回点到三角形的最短距离。 三角形三个点为（A，B，C），另外一点为P 思路是：利用面积来计算 如果点在三角形内： 则该点P与点ABC组成的三角形PAB，PAC，PBC面积之和等于ABC，包括点在边上的情况。 如果点在三角形外： 则计算PAB，PAC，PBC的面积和ABC的面积以及各边边长，利用面积等于底×高/2，可以求出距离d。点到AB的距离dAB： dAB=2*PAB/AB； PAB表示三角形PAB的面积
点到三角形的距离---最快的计算方式
weixin_38977362的博客
02-10 3207
点到三角形距离的数学原理： 所有的求点ppp到三角形的距离的方式数学本质上都是一样的： 第一步：找到点在三角形所在平面的投影点p′p'p′。 第二步：将p′p'p′再向三角形上做一次投影得到p′′p''p′′： 如果p′p'p′直接落在三角形内，直接令p′′=p′p''=p'p′′=p′。 如果落在三角形外，再依次判断投影在哪条边上，如果投影点落在边上就计算出来p′′p''p′′，如果超出了边的范围，直接取顶点作为p′′p''p′′的计算值。 第三步：计算p−p′′p-p''p−p′′的长度，即为点到三角形
PPCA EM理解
长虹剑的专栏
09-14 2787
近期做人脸注册,发现直接用NICP的结果进行PCA时会有比较大的噪声, 想试试用PPCA, 并看能否在此基础上把 pose 也当作隐变量加入. (一般这种具有复杂的公式而且还是看别人博客的笔记我是不愿意放在CSDN可是我的印象笔记突然不能登录了) 推公式的部分基础知识 高斯分布相乘 PPCA 详细的话先看 数据降维 找其中的第六章 PRML读书笔记：Probabilistic PCA 观测样本 x...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值