数据分析｜指标体系中的标准化方法

总体来说，可以将标准化方法分为两类：一类是定距的，即保留数据之间距离；一类是定序的，即不保留数据之间实际距离，只保留大小关系。

1 保留数据的实际距离的标准化方法

当需要保留数据之间距离时，需要包括三种类型的方法：

• 对数据进行扭曲，扩大样本值在某个范围内的差距；
• 对数据进行缩放，调整样本值的均值和标准差；
• 将样本值固定在指定范围内。

1.1 【缩放】方差标准化（扭曲数据真实距离）

通过标准化，令数据的平均值为 $0$，标准化为 $1$ 的标准化方法，在社会学、传播学研究中使用普遍，公式如下：
$${\hat{x}}_i=\frac{x_i-\mu }{\sigma },x\in R,\hat{x}\in R$$
其中 $\mu$ 为样本均值，$\sigma$ 为样本标准差。

优点：

• 保留数据真实距离，维持标准化前数据分布，缩放均为等比例缩放。
• 标准化后数据的平均值为 $0$，标准化为 $1$。
• 对极值不敏感。

缺点：

• 标准化后数据不在固定范围内，如用作指标体系计算还需要进一步标准化。
• 样本标准化后值不稳定，受样本平均值和标准差影响；当添加新样本时，旧样本的标准化值一定发生变化。

扩展方法：

• 可以在标准化后再进行离差标准化，从而使标准化后的最小值一定为 $0$，最大值一定为 $1$。

样例：

1.2 【缩放】离差标准化（呈现数据真实距离）

如果需要保留数据真实距离的话，可以使用极差标准化，公式如下：
$${\hat{x}}_i=\frac{x_i-\min (x)}{\max (x)-\min (x)},x\in R,\hat{x}\in [0,1]$$
优点：

• 保留数据真实距离，维持标准化前数据分布。
• 标准化后的最小值一定为 $0$，最大值一定为 $1$。

缺点：

• 样本标准化后值不稳定，受样本最大值和最小值影响；当添加新样本时，旧样本的标准化值可能发生变化。
• 对极值非常敏感。

扩展方法：

• 可以将 $\min (x)$ 和 $\max (x)$ 固定，从而解决标准化后样本值不稳定的问题，但这样处理可能会导致出现标准化后小于 $0$ 或大于 $1$ 的值；也可以考虑将 $\min (x)$ 固定为 $0$。

样例：

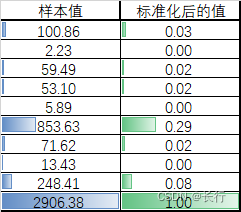
1.3 【先扭曲，再缩放】Log 标准化（扭曲数据真实距离）

如果数据的分布呈现现显著地长尾分布，样本的最大值比样本的最小值高出了数量级，可以使用 Log 标准化，公式如下：
$${\hat{x}}_i=\frac{{\log }_a(x_i+1)}{{\log }_a\max (x+1)},x>0,\hat{x}\in [0,1]$$
其中对数底数可以根据需要缩放的量级进行调整，常见的可以使用自然对数或以10为底的对数。

优点：

• 扭曲了原数据，扩大（加强）了较小样本值之间的差距，缩小（减弱）了较大样本值之间的差距。
• 对极大值不太敏感。
• 标准化后的最大值一定为 $1$。

缺点：

• 样本标准化后值不稳定，受样本最大值和最小值影响；当添加新样本时，旧样本的标准化值可能发生变化。
• 最小值后的最小值不一定为 $0$。

样例：

1.4 【先扭曲，再缩放】Log 标准化 + 离差标准化（扭曲数据真实距离）

如果需要使用 Log 标准化，且需要令标准化后的最小值为 $0$，最大值为 $1$，可以在 Log 标准化的基础上融合离差标准化。相当于对极差标准化进行了扭曲，拉伸了样本值较小部分，压缩了样本值部分。公式如下：
$${\hat{x}}_i=\frac{{\log }_a(x_i+1)-{\log }_a\min (x+1)}{{\log }_a\max (x+1)-{\log }_a\min (x+1)},x>0,\hat{x}\in [0,1]$$
优点：

• 扭曲了原数据，扩大（加强）了较小样本值之间的差距，缩小（减弱）了较大样本值之间的差距。
• 对没有跨越量级的极大值不敏感。
• 标准化后的最小值一定为 $0$，最大值一定为 $1$。

缺点：

• 样本标准化后值不稳定，受样本最大值和最小值影响；当添加新样本时，旧样本的标准化值可能发生变化。

扩展方法：

• 可以将 $\min (x)$ 和 $\max (x)$ 固定，从而解决标准化后样本值不稳定的问题，但这样处理可能会导致出现标准化后小于 $0$ 或大于 $1$ 的值。

样例：

1.5 Sigmoid 函数标准化（扭曲数据真实距离）

如果数据呈现中间集中的分布，同时需要将区分中心部分的差距，可以使用 Sigmod 函数进行标准化，公式如下：
$${\hat{x}}_i=\frac{1}{1+e^{-(x_i-a)\times b}},x\in R,\hat{x}\in (0,1)$$
其中系数 $a$ 为需要区分部分中心的值，系数 $b$ 为需要区分的程度。

优点：

• 扭曲了原数据，扩大（加强）了某个中心附近的样本值之间的差距，缩小（减弱）了距离该中心较远的样本值之间的差距。
• 对极小值和极大值均完全不敏感。
• 样本标准化后的值稳定，不受样本最大值和最小值的影响。

缺点：

• 对距离中心较远的样本值之间的差距 非常 不敏感。

样例：

1.6 【先扭曲，再缩放】EXP 标准化（扭曲数据真实距离）

相反于 1.3，如果需要扩大大样本之间的差距，可以使用 EXP 进行缩放，公式如下：
$${\hat{x}}_i=\frac{e^{x_i}-e^{\min (x)}}{e^{\max (x)}-e^{\min (x)}},x\in R,\hat{x}\in [0,1]$$
其中自然对数也可以根据需要缩放的量级进行调整。

优点：

• 扭曲了原数据，缩小（减弱）了较小样本值之间的差距，扩大（增强）了较大样本值之间的差距。
• 对极大值 非常 敏感。
• 标准化后的最小值一定为 $0$，最大值一定为 $1$。

缺点：

• 样本标准化后值不稳定，受样本最大值和最小值影响；当添加新样本时，旧样本的标准化值可能发生变化。

样例：

2 保留数据的大小关系的标准化方法

2.1 使用排名的标准化

如果不需要保留数据之间真实数据，只需要保留大小关系的话，可以直接使用样本值的排名，公式如下：
$${\hat{x}}_i=\frac{rank{x}_i-1}{len(x)-1},x\in R,\hat{x}\in [0,1]$$
优点：

• 样本在 $[0,1]$ 内均匀分布。
• 标准化后的最小值一定为 $0$，最大值一定为 $1$。
• 对极值 完全不 敏感。

缺失：

• 不再保留原数据的真实数据。

样例：

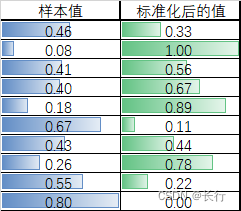
2.2 扭曲排名的标准化

在 2.1 的基础上，可以使用 1 中扭曲数据的方法，对排名进行扭曲，突出强调某一段的排名差异。

3 指标体系的实践中的问题

3.1 指标权重 $\ne$ 指标区分能力

当使用标准化后的数据作为指标体系中的指标时，需要注意每个指标的实际区分能力，在受指标权重确定的基础上，也受到标准化后数据分布的影响。即使通过标准化方法，令数据的最小值为 $0$，最大值为 $1$ 后也仍然存在这种影响。例如：

在上例中，指标1 使用离差标准化，指标 2 使用 Log 标准化 + 离差标准化。可以发现，指标 1 对于除了样本 6 和样本 10 以外的其他样本，因得分过小而意义不大；而指标 2 对每个样本都相对有意义。此时，假设指标 1 和指标 2 的指标权重相同，但是其区分能力也是有所差距的。

3.2 指标对不同样本的敏感程度差异

同样适用 3.1 样例。如果某个月中，样本 2 在指标 1 上提升了 10 倍，对于对其在指标体系计算的得分也没有什么影响，这种变化是不敏感的；而如果样本 10 在指标 1 上提升了 10%，那么其他样本的得分均要降低 10%，这种变化是相对敏感的。

3.3 指标的纵向（时间维度）对比问题

如果指标数据在标准化过程中，使用了数据最大值或最小值参与标准化，则会导致数据中每个样本不能纵向对比，即指数降低不一定意味着数据绝对值的下降，也可能是因为其增长速度低于其他样本或受到不同指标对样本的敏感程度的差异导致。

但是如果不使用数据最大值或最小值参与标准化，则如何将最终指数控制在指定范围内（例如百分制）则相对困难，这里需要研究者进行取舍。