TDDFT计算软件Octopus学习笔记(六)： 电极化率和响应函数(Diamond)

本文以金刚石为例，计算其电极化率chi(w)和响应函数R(t)。

1. 基态计算

对于金刚石，无法使用+U方法来扩展其能带带隙，因此使用metaGGA方法来扩展带隙至4.96eV，具体细节在学习笔记(四)中。 先用以下inp文件计算基态信息。

CalculationMode =  gs
ExperimentalFeatures = yes
FromScratch = yes
PeriodicDimensions = 3
BoxShape = parallelepiped
ParKPoints = auto
XCFunctional = mgga_x_tb09 + lda_c_pw
FilterPotentials = filter_none

a = 3.57*angstrom  #2.527/sqrt(2)
Spacing = 0.20

%LatticeParameters
  a | a | a
%

%LatticeVectors
 0.0 | 0.5 | 0.5
 0.5 | 0.0 | 0.5
 0.5 | 0.5 | 0.0
%
%ReducedCoordinates
 "C" |   0.0    | 0.0     | 0.0
 "C" |   3/4    | 3/4     | 3/4
%
nk = 16
%KpointsGrid
 nk | nk | nk
%

KPointsUseSymmetries = yes
%SymmetryBreakDir
 1 | 0 | 0
%

2. 时间依赖计算

再以如下inp文件进行时间依赖计算。

CalculationMode =  td
ExperimentalFeatures = yes
FromScratch = yes
PeriodicDimensions = 3
BoxShape = parallelepiped
ParKPoints = auto
XCFunctional = mgga_x_tb09 + lda_c_pw
FilterPotentials = filter_none

a = 3.57*angstrom  #2.527/sqrt(2)
Spacing = 0.2

%LatticeParameters
  a | a | a
%

%LatticeVectors
 0.0 | 0.5 | 0.5
 0.5 | 0.0 | 0.5
 0.5 | 0.5 | 0.0
%
%ReducedCoordinates
 "C" |   0.0    | 0.0     | 0.0
 "C" |   3/4    | 3/4     | 3/4
%
nk = 16
%KpointsGrid
 nk | nk | nk
%

KPointsUseSymmetries = yes
%SymmetryBreakDir
 1 | 0 | 0
%

%GaugeVectorField
1.0|0.0|0.0
%

PropagationSpectrumMaxEnergy= 50*eV

ExtraStates=0
TDExponentialMethod = lanczos
TDExpOrder = 16

TDPropagator = etrs
TDStepsWithSelfConsistency = all_steps

TDTimeStep = 0.01
TDPropagationTime = 200

一些说明：

1. PropagationSpectrumMaxEnergy 确定了输出的光谱频率范围，默认是0~20eV， 可以任意修改，这里我重新设定其为50eV，注意乘号*不可省略。 更大的频率范围可以得到更精确的频域积分。
2. TDTimeStep 需要先进行收敛计算，具体方法是不施加任何外场，计算自由传播，这样总能量在传播过程中应该不变，但是大的时间步由于误差的积累放大会导致能量在传播过程中逐渐发散乃至于NaN。一般可选其自由传播200步即可。然后计算第一步和第200步的能量差值，做收敛图如下，然后再选择合适的时间步骤：

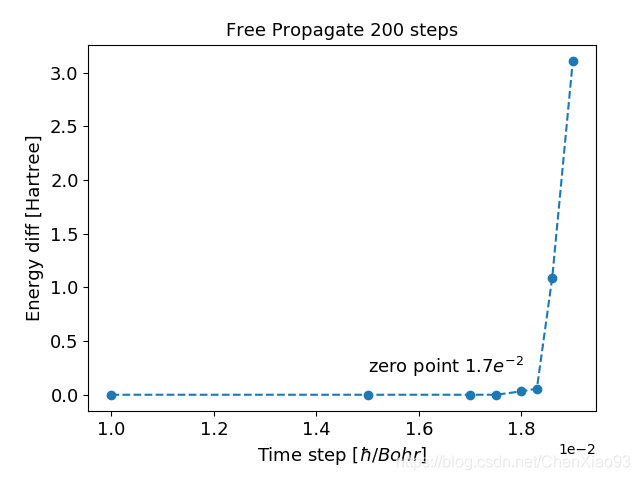
3. TDPropagationTime也会影响计算结果，同样需要计算收敛， 可以分别计算传播时间为50,100,200[hbar/Hartree], 之后比较它们的介电函数与真实介电函数差别。
4. 真实介电函数数据可以查询文献中的图，再通过 Getdada 程序， 从图中读取数据，这样就可以和自己的数据画在一起进行比较。
5. k点取样密度同样会影响计算结果。 由于数值误差，在光谱频率小于带隙能量时，介电函数的虚部本应该为零，证明无吸收，但是在低密度k点抽样时，在这个光谱频率处，会出现错误的吸收峰。可以通过增加k点密度来修正。
6. GaugeVectorField 块结构的第一行，标示出了微扰规范场的方向和大小，大小也会强烈的影响计算结果，大的场强显然会偏离线性响应，并且在介电函数虚部的小于带隙处也会出现峰。
7. 下面这两行表示了对于exp算符的近似方法，默认为4阶Taylor展开方法，但经过实验验证，laczos方法和16阶这种搭配会给出最好的结果，允许我们选用更大的时间步并且相对最经济的计算时间。

TDExponentialMethod = lanczos
TDExpOrder = 16

3. 运行小程序

计算完成后，运行 Octopus 自带的 oct-dielectric-function 小程序，则会从 multipoles 文件中读取数据并计算，之后同时输出 电极化率chi(w) 和 介电函数 epsilon(w) 在 ./td.general 文件夹中。 响应函数可以从电极化率的傅里叶变换中得出：

这里需要注意，积分内的变换因子也可能是exp(iwt), 因为从多极子multipoles文件计算电极化率chi(w)的时候也经过了一次傅里叶变换，还不确定那次变换使用的是exp(iwt)还是exp(-iwt)。

最终得到响应函数，取其实部即可：