最近看论文,发现一个很不错的概率密度估计方法。在此小记一下。
先来看看准备知识。
密度估计经常在统计学中作为一种使用有限的样本来估计其概率密度函数的方法。
我们在研究随机变量的过程中,随机变量的概率密度函数的作用是描述随机变量的特性。(概率密度函数是用来描述连续型随机变量取值的密集程度的,举例:某地某次考试的成绩近似服从均值为80的正态分布,即平均分是80分,由正态分布的图形知x=80时的函数值最大,即随机变量在80附近取值最密集,也即考试成绩在80分左右的人最多。)但是在实际应用中,总体概率密度函数通常是未知的,那么如何来估计总体概率密度呢?一般,我们通过抽样或者采集一定的样本,可以根据统计学知识从样本集合中推断总体概率密度。这种方法统称为概率密度估计,即根据训练样本来确定随机变量的概率分布。一般概率密度估计方法方法大致分为两类:参数估计和非参数估计。
参数估计(Parametric Estimation)是根据对问题的经验知识,假设问题具有某种数学模型 ,随机变量服从某种分布,即先假定概率密度函数的形式,然后通过训练数据估计出分布函数的参数。常见的参数估计方法有极大似然估计方法和贝叶斯估计方法。对于参数估计,根据样本中是否已知样本所属类别(即是否带标签)将参数估计又划分为监督参数估计和非监督参数估计。监督参数估计是由 已知类别的样本集对总体分布的某些参数进行统计推断 。而无监督参数估计已知总体概率密度函数形式但未知样本所属的类别,要求推断出概率密度函数的某些参数 ,这种推断方法称之为非监督情况下的参数估计。
非参数估计(Nonparametric Estimation)是在已知样本所属的类别不假定总体分布形式下, 基于大样本的性质,直接利用样本估计出整个函数。在很多情况下,我们对样本的分布并没有充分的了解,无法事先给出密度函数的形式,而且有些样本分布的情况也很难用简单的函数来描述。在这种情况下,就需要用到非参数估计。但是,并不是非参数估计一定优于参数估计,因为非参数估计受训练样本影响,其完备性或泛化能力不会很好;且这种估计只能用数值方法取得,无法得到完美的封闭函数图形。常用的非参数估计方法有直方图法,核概率密度估计等。
(若有闲暇,后续将极大似然、贝叶斯估计等等估计方法详细总结)
这里说说核密度估计方法(也有称之为
Parzen
窗法)
进入正题
核密度估计的形式:
这里 K(x) 是 核函数(非负,积分为1,均值为0,符合概率密度的性质), h>0 是带宽。有很多种核函数, uniform,triangular,biweight,triweight,Epanechnikov,normal 等。各种核函数的图形如下:
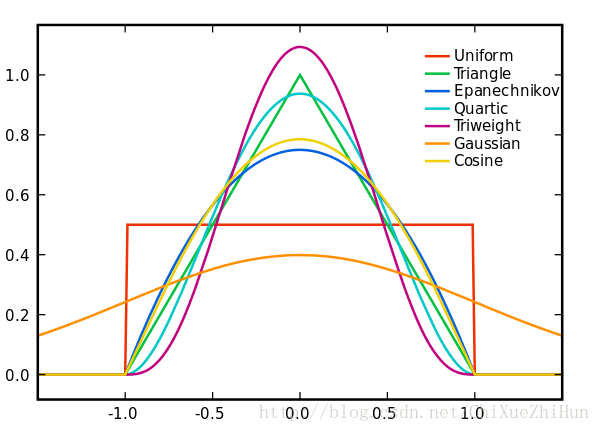
由于高斯内核方便的数学性质,也经常使用 K(x)=ϕ(x) , ϕ(x) 为标准正态概率密度函数。核密度估计与直方图很类似,但相比于直方图还有光滑连续的性质。
举例理解(该例子来自维基百科 https://en.wikipedia.org/wiki/Kernel_density_estimation)
已知:6个数据点
x1=−2.1,x2=−1.3,x3=−0.4,x4=1.9,x5=5.1,x6=6.2
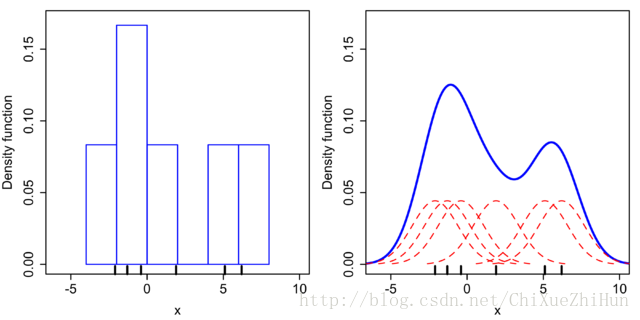
对于直方图,首先将水平轴划分为覆盖数据范围的子间隔或区段。在这种情况下,我们有6个宽度为2的矩形。每当数据点落在此间隔内时,我们放置一个高度为 112 的矩形。对于核密度估计,我们在每个数据点 xi 上放置方差2.25(由红色虚线表示)的正态核函数。叠加一起得到核密度估计的结果,蓝色线表示。
很明显,直方图得到的密度估计平滑程度比使用核密度估计得到的密度函数要差很多.
现在问题是如何选定核函数的“方差”呢?这其实是由 h 来决定,不同的带宽
核带宽的选择
带宽是一个自由参数,对所得到的估计值有很大的影响。为了说明效果,举个例子:
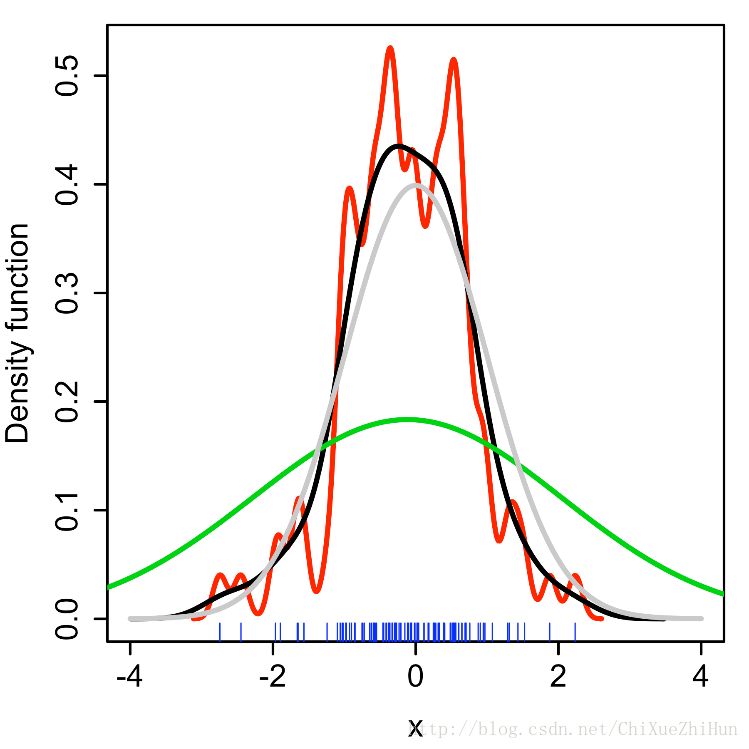
下图是从标准正态分布中抽取的随机样本(横轴上的蓝色的点点代表样本点)灰色曲线是真是的概率密度(正态密度,均值0,方差1)。相比之下,红色曲线是使用了过小的带宽 h(=0.05) 得出的概率密度曲线,可见其波折陡峭;绿色曲线过于平滑,因为它使用了过大的带宽 h(=2) ,掩盖了数据大部分基础结构。
那么对于
h
的选择可以使用最小化L2风险函数(即平均积分平方误差,mean intergrated squared error)。
在
weakassumptions
下,
MISE(h)=AMISE(h)+o(1nh+h4)
,其中
AMISE
为渐进的
MIS
E。而
AMISE
有,
其中,
为了使 MISE(h) 最小,则转化为求极点问题,
当核函数确定之后, hAMISE 公式里的 R 、
如果使用高斯核函数进行核密度估计,则
h
的最优选择(即使平均积分平方误差最小化的带宽)为
这里 σ^ 是样品的标准差。这种近似称为正态分布近似,高斯近似,或Silverman(1986)经验法则。虽然这个经验法则很容易计算,但应谨慎使用,因为当密度不接近正态时,可能会产生泛化极差的估计。该经验法则推导过程详见:Silverman, B.W. (1986). Density Estimation for Statistics and Data Analysis. London: Chapman & Hall/CRC. p. 48. ISBN 0-412-24620-1.
这里带宽的作用简述:
1.在数据可视化的相关领域中,带宽的大小决定了核密度估计函数(KDE)的平滑(smooth)程度,带宽越小越undersmooth,带宽越大越oversmooth。(详细解释)
2.在POI兴趣点推荐领域,或位置服务领域,带宽 h 的设置主要与分析尺度以及地理现象特点有关。较小的带宽可以使密度分布结果中出现较多的高值或低值区域,适合于揭示密度分布的局部特征,而较大的带宽可以在全局尺度下使热点区域体现得更加明显。另外,带宽应与兴趣点的离散程度呈正相关,对于稀疏型的兴趣点分布应采用较大的带宽,而对于密集型的兴趣点则应考虑较小一些的带宽。
如果带宽不是固定的,而是根据样本的位置而变化(其变化取决于估计的位置(balloon estimator)或样本点(逐点估计pointwise estimator)),则会产生一种特别有力的方法,称为自适应或可变带宽的核密度估计。就POI兴趣点推荐来说,由于密集的城市地区的签到密度很高,人烟稀少的农村地区的签到密度较低。就是说不同位置应该采取不同的分析尺度,因此本文采用不固定的带宽来进行核密度估计。
说到这, 有些朋友可能不知道POI兴趣点推荐是啥意思, 这里简单的说一下:POI是Point-of-Interest的意思,即兴趣点。就是说,给用户推荐其感兴趣的地点。就这么简单。在推荐系统相关领域,兴趣点推荐是一个非常火爆的研究课题。这里会用到核密度估计的方法,比如这篇论文:Jia-Dong Zhang,Chi-Yin Chow.(2015)GeoSoCa: Exploiting Geographical, Social and Categorical Correlations for Point-of-Interest Recommendations.SIGIR’15, August 09 - 13, 2015, Santiago, Chile.就利用了可变带宽的核密度估计方法。
这里再简单讨论一下自适应带宽的核密度估计方法。自适应带宽的核密度估计方法是在固定带宽核密度函数的基础上,通过修正带宽参数为而得到的,其形式如式所示:
这里
k(x)
是带宽为
hj
的核密度估计函数,
M
是样例的个数,看出来了吧,每一个点
自适应带宽的核密度估计可以参考维基百科:https://en.wikipedia.org/wiki/Variable_kernel_density_estimation
推荐帖子:http://blog.sina.com.cn/s/blog_62b37bfe0101homb.html
参考资料
https://en.wikipedia.org/wiki/Kernel_density_estimation
https://www.zhihu.com/question/20212426/answer/74989607
https://en.wikipedia.org/wiki/Variable_kernel_density_estimation
http://www.tuicool.com/articles/EVJnI3
袁修开,吕震宙,池巧君. 基于核密度估计的自适应重要抽样可靠性灵敏度分析.西北工业大学学报.Vol.26 No.3.2008.6.


























 1092
1092

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








