
BP(反向传播算法)公式推导及例题解析
写在前面:最近赶上《模式识别》课程考试,就把BP重新复习了下。猜测老师可能会出这方面的计算题(hhh,也是不知道我哪里来的自信),就学习了Matt Mazur博客的例题。
(再加一句废话:其实在我之前,已经有前辈
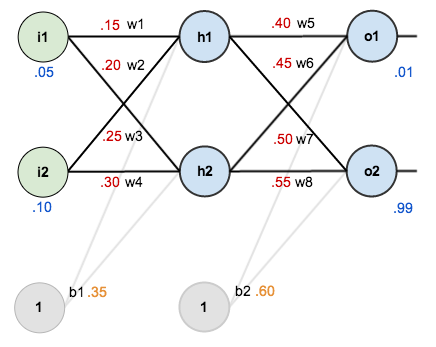
写过了,觉得还是有必要自己推,所以就画蛇添足了)这里我们使用两个输入、隐含层两个神经元、两个输出,其中隐含层和输出层都有偏置,结构如下:


为了能够保证传播过程的顺利进行,这里对参数进行了初始化:

前向传播
隐含层
这里我们先计算 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/90e10fdc47fd9181c9e4881846fd03e6.png) 的输入:
的输入:


之后将输入传递给激活函数(这里使用的是sigmoid激活函数),得到:


同理,可以得到 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/b364285cde706d89322f8d32d32cc569.png) 的结果:
的结果:


输出层
将隐含层的输出作为输入,对输出层的神经元重复上述过程。
![[公式]](https://i-blog.csdnimg.cn/blog_migrate/0ad503d494306672412146dec3bbb165.png) 的输出如下:
的输出如下:


同理可以得到 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/f0a887a6e67a9b7337e2d99da91d6172.png) 的输出:
的输出:


误差计算
这里我们均方误差作为目标函数:

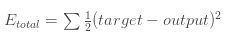
有了output,之后分别计算 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/0ad503d494306672412146dec3bbb165.png) 和
和 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/f0a887a6e67a9b7337e2d99da91d6172.png) 的误差:
的误差:
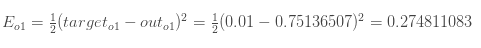
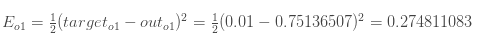
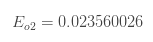

则,总误差为:
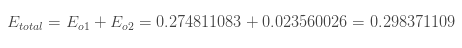

反向传播
反向传播是根据链式求导法则对参数( ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) )进行更新。
)进行更新。
输出层-->隐含层
(1) ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 的更新
的更新


进一步解释:

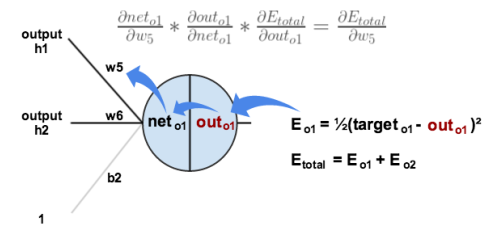
为了求出 的梯度,我们需要计算上式的每个因子。
首先计算对 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/7a94dacd53d02799805c92487e890296.png) 的梯度:
的梯度:
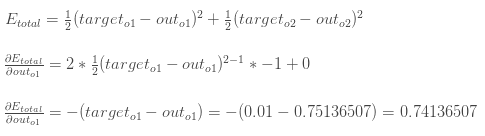

其次计算对 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/96515634a3c908f1febf632e76c8cf2e.png) 的梯度:
的梯度:


之后计算对 的梯度:


最后得到的 的梯度就是上式三个因子的乘积:


这里将学习率设为0.5,更新之后的 为:
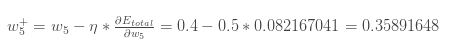

同理,可对 完成一次更新:


(2) 的更新
(结构图显示每层共用一个偏置,但是个人觉得每个神经元的偏置计算结果应该是不一样的,故应该分别进行更新,这里只对第一个神经元的偏置更新进行说明,下同)
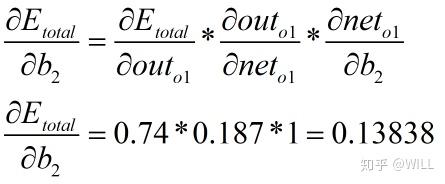
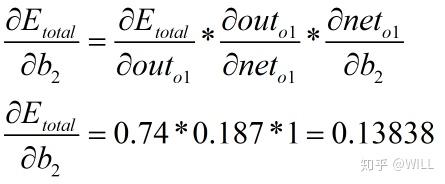
得到一个更新之后的 为:


隐含层-->输入层
(1) ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 的更新
的更新
对于 的梯度,我们需要计算出:

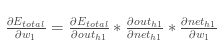
更进一步说明:

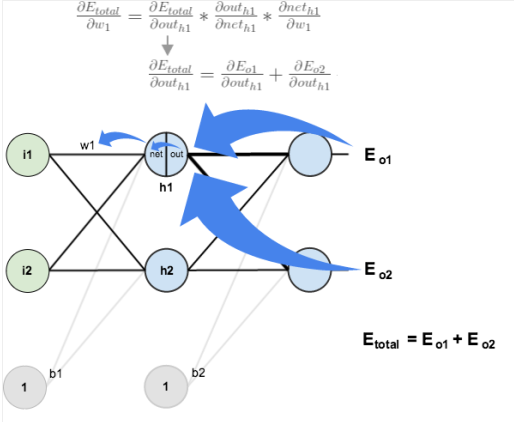
根据上图,我们知道 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/61107aae9051b969b7303d012e718613.png) 对
对 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/7a94dacd53d02799805c92487e890296.png%E3%80%81out_%7Bo2%7D) 都有作用,因此:
都有作用,因此:


先计算上式第一个因式
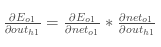



而

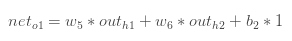
所以
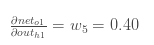

将它们相乘得到:
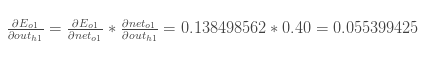

同理,对第二个因式


因此

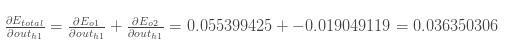
之后,我们可以得到




这样,就得到了 的梯度


更新之后的


同理,我们可以得到其余更新后的w


(2) 的更新


可得 的梯度

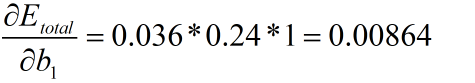
则,完成一次更新后的 为


这样,我们就完成了一次前向传播和反向传播。
注:除偏置更新的图片外,其余图片均来自Matt Mazur博客。

分享
分享
推荐阅读
-

BP反向传播矩阵推导图示详解
神经网络BP算法推导
2019-6-28——更新: https://github.com/yjh0410/NeuralNetwork简单说明一下: NeuralNetwork.py是核心代码,实现了神经网络的定义,包括前向传播和反向传播,训练代码等等。 三个demo文件…
神经网络BP反向传播算法推导
本文详细给出了用于神经网络训练的反向传播(Back Propagation)算法的证明推导过程。过程虽然有点繁琐,却并未涉及到复杂的数学变换,所需要的仅是基本的导数和矩阵运算知识,以及耐心。 …
BP神经网络公式推导(含代码)
什么是BP神经网络BP(Back Propagation)神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络,它的基本思想是梯度下降法,利用梯度搜索技术,以期使网络的 实际输出值和期望输…
























 538
538











25 条评论
EdisonGzq:深度学习---反向传播的具体案例,哈哈哈这个才是原版吧
说实话,写得一般般。应该从误差定义,反传,再梯度更新开始讲。注重逻辑啊。不要陷入细节。
b2更新有问题吧
写的非常棒
在每一轮迭代过程中,可以理解为权重w以及阈值b是并行更新的
很详细的推导,手动点赞
EdisonGzq:深度学习---反向传播的具体案例,作者您好!你这是完全copy我的丫。没看到你重新推到的,错误都是相同的呢
之后看到前辈已经进行了这个工作,遂对前辈的工作在文章开头也进行了引用。
只是学习了相同的文章,相同的内容,如果前辈认为copy或者侵权的话,还请告知哈。
没事,只是今天突然看到,知识大家一起分享,没事
Eo2对b2的导数怎么没算? 还有你计算的0.138,下面咋成了0.039
偏导公式中Eo1应该换为Etotal,对b2的偏导结果不变,仍为0.13838;最后更新后的b2值应为0.6-0.5*0.13838=0.53081。
稍后会在正文中进行更正。
感谢指正,表述是有些不当,现已更正。