【经典算法实现 30】图的创建 --- 十字链表法

之前写了这么多树的文章，本文要开始学习图了，先来随便画个图：

问题来，如果要在C语言代码中保存这幅图，应该如何保存呢？

本文主要目的，就是通过十字链表法来实现这幅图的保存 及 遍历。

本文图的ppt 及 c 代码源文件，已上传《图的创建 — 十字链表法.zip》
本文链接： https://blog.csdn.net/Ciellee/article/details/108199838

一、十字链表法

我们先来画图，使用十字链表法，将前面的图画出来。

1.1 画出所有顶点

顶点结点的数据类型为

// 顶点结构 
typedef struct pNode{
	char data;				// 顶点字符，如 A
	struct sNode *firstIn;	// 入边结构体指针链表， 指向第一条入边的结构体指针
	struct sNode *firstOut; // 出边结构体指针链表， 指向第一条出边的结构体指针
}pNode;

好，开始根据数据类型画图吧，（带*说明是指针）

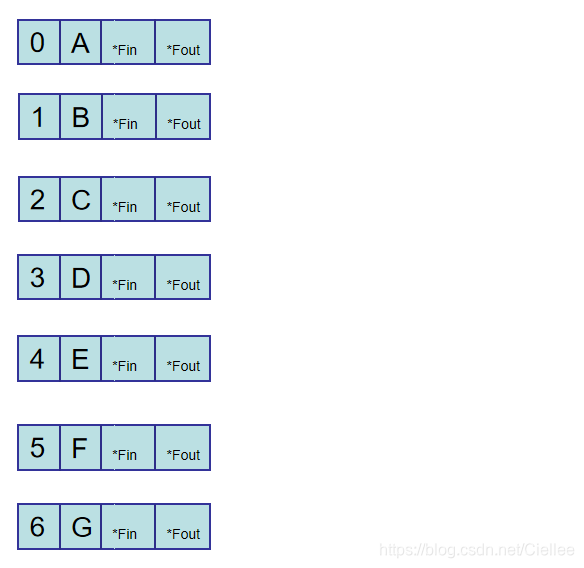
1.2 画出所有的边

边的数据类型为

// 边结点结构
typedef struct sNode{
	char tailvex;			// 该边的起点， 如 A->B 这条边，此处保存 A	
	char headvex;			// 该边的终点， 如 A->B 这条边，此处保存 B	
	struct sNode *tlink;	// 出表指针链表，指同起点所有边的链表，比如 A->B 和 A->C，它们的起点相同都是A
 	struct sNode *hlink;	// 入表指针链表，指同终点的所有边的链表，比如 B->D 和 C->D，它们的终点相同都是D
}sNode;

好，开始根据数据类型画图吧，（带*说明是指针）

1.3 完善边与顶点的出边关系

下图，蓝包的为顶点，紫色的为边，可以看出，通过紫线把所有的顶点与边都边接起来了。

1.4 完善边与顶点的入边关系

加上下图红色的虚线，这样看起来，就复杂了许多

至此，我们最开始的图，使用十字链表法就实现好了。

下面，我用代码把它表示出来。

二、十字链表代码实现

// 十字链表法实现图的保存 

#include <stdio.h>

// 边结构体 
typedef struct sNode{
	char tailvex;			// 该边的起点， 如 A->B 这条边，此处保存 A	
	char headvex;			// 该边的终点， 如 A->B 这条边，此处保存 B	
	struct sNode *tlink;	// 出表指针链表，指同起点所有边的链表，比如 A->B 和 A->C，它们的起点相同都是A
 	struct sNode *hlink;	// 入表指针链表，指同终点的所有边的链表，比如 B->D 和 C->D，它们的终点相同都是D
}sNode;

// 顶点结构体 
typedef struct pNode{
	char data;				// 顶点字符，如 A
	struct sNode *firstIn;	// 入边结构体指针链表， 指向第一条入边的结构体指针
	struct sNode *firstOut; // 出边结构体指针链表， 指向第一条出边的结构体指针
}pNode;

#define pNode_Num  	7		// 7个顶点 
#define sNode_Num  	9		// 9条边 
const char c_char[pNode_Num] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'}; 
const char s_char[sNode_Num][2]={ 
				{'A','B'}, 	{'A','C'}, 
				{'B','D'}, 	{'B','A'}, 
				{'C','D'}, 
				{'D','E'},  {'D','F'}, 
				{'E','G'}, 
				{'F','C'}};

// 创建边
sNode ** Create_sNode(){
	int i;
	sNode **s;
	s = (sNode **)malloc(sizeof(sNode *) * sNode_Num);
	for(i = 0; i<sNode_Num; i++){
		s[i] = (sNode *)malloc(sizeof(sNode));
		s[i]->tailvex = s_char[i][0];
		s[i]->headvex = s_char[i][1];
		s[i]->tlink = NULL;
		s[i]->hlink = NULL;
		printf("sNode[%d]: \'%c\'->\'%c\' - %p - %p\n",i, s[i]->tailvex, s[i]->headvex, s[i]->tlink, s[i]->hlink); 
	}
	printf("\n\n");
	return s;
}

// 创建顶点 
pNode ** Create_pNode(sNode **s){
	int i, j;
	pNode **p;
	sNode *s_tmp=NULL; 
	p = (pNode **)malloc(sizeof(pNode *) * pNode_Num);
	for(i = 0; i<pNode_Num; i++){
		p[i] = (pNode *)malloc(sizeof(pNode));
		p[i]->data = c_char[i];
		p[i]->firstIn = NULL;
		p[i]->firstOut = NULL;
		
		// 找出当前节点所有的出边，以当前节点为起始点
		for(j = 0; j<sNode_Num; j++){ 
			if(p[i]->data == s[j]->tailvex)
			{
				if(p[i]->firstOut == NULL){
					p[i]->firstOut = s[j];
					s_tmp = p[i]->firstOut;
				}
				else{
					s_tmp->tlink = s[j];
				}

			}
		} 
		
		// 找出当前节点所有的入边，以当前节点为起始点
		for(j = 0; j<sNode_Num; j++){ 
			if(p[i]->data == s[j]->headvex)
			{
				if(p[i]->firstIn == NULL){
					p[i]->firstIn = s[j];
					s_tmp = p[i]->firstIn;
				}
				else{
					s_tmp->hlink = s[j];
				}
				
			}
		} 
		
		// 打印节点关系 
		printf("pNode[%d]: \'%c\' - %p - %p\nfirstIn : ",i, p[i]->data, p[i]->firstIn, p[i]->firstOut); 
		s_tmp = p[i]->firstIn;
		while(s_tmp != NULL){
			printf(" --> [\'%c\'->\'%c\']", s_tmp->tailvex, s_tmp->headvex); 
			s_tmp = s_tmp->hlink; 
		}
		printf("\nfirstOut: ");
		s_tmp = p[i]->firstOut;
		while(s_tmp != NULL){
			printf(" --> [\'%c\'->\'%c\']", s_tmp->tailvex, s_tmp->headvex); 
			s_tmp = s_tmp->tlink; 
		}
		printf("\n\n\n");
	}
	printf("\n\n");
	return p;
} 


int main()
{
	// 创建边 
	sNode **s = Create_sNode();
	
	// 创建顶点 
	pNode **p = Create_pNode(s);
	
 	// 打印节点及其关系 
	
	return 0;
}

2.1 运行结果

结合前面的 1.4 中的图，可以看出，图的关系已经正确的创建好了。

sNode[0]: 'A'->'B' - 00000000 - 00000000
sNode[1]: 'A'->'C' - 00000000 - 00000000
sNode[2]: 'B'->'D' - 00000000 - 00000000
sNode[3]: 'B'->'A' - 00000000 - 00000000
sNode[4]: 'C'->'D' - 00000000 - 00000000
sNode[5]: 'D'->'E' - 00000000 - 00000000
sNode[6]: 'D'->'F' - 00000000 - 00000000
sNode[7]: 'E'->'G' - 00000000 - 00000000
sNode[8]: 'F'->'C' - 00000000 - 00000000


pNode[0]: 'A' - 00B20E48 - 00B20E00
firstIn :  --> ['B'->'A']
firstOut:  --> ['A'->'B'] --> ['A'->'C']


pNode[1]: 'B' - 00B20E00 - 00B20E30
firstIn :  --> ['A'->'B']
firstOut:  --> ['B'->'D'] --> ['B'->'A']


pNode[2]: 'C' - 00B20E18 - 00B20E60
firstIn :  --> ['A'->'C'] --> ['F'->'C']
firstOut:  --> ['C'->'D']


pNode[3]: 'D' - 00B20E30 - 00B20E78
firstIn :  --> ['B'->'D'] --> ['C'->'D']
firstOut:  --> ['D'->'E'] --> ['D'->'F']


pNode[4]: 'E' - 00B20E78 - 00B20EA8
firstIn :  --> ['D'->'E']
firstOut:  --> ['E'->'G']


pNode[5]: 'F' - 00B20E90 - 00B20EC0
firstIn :  --> ['D'->'F']
firstOut:  --> ['F'->'C']


pNode[6]: 'G' - 00B20EA8 - 00000000
firstIn :  --> ['E'->'G']
firstOut:

《[数据结构]十字链表结构与画图》
《[数据结构]一篇文章了解邻接图和邻接表》