逻辑回归中的代价函数

了解误差成本函数是如何实现的。举一个模型带有训练集，和之前一样设m来表示训练示例的数量，每个训练样本都有一个或多个特征，共有n个特征由于这是一个二元分类任务，目标标签y只取两个值0或1.最后逻辑回归模型由该方程定义在这个训练集中如何选择参数w和b？回想一下线性回归，这是平方误差成本函数。唯一改变的是我把一半放在里面求和而不是求和之外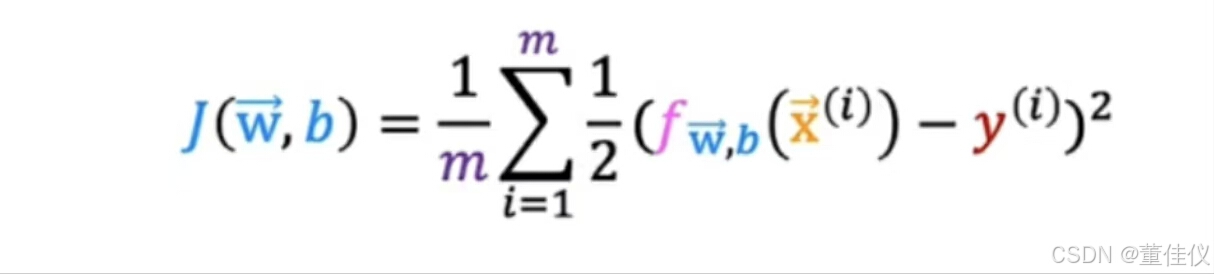您可能还记得在线性回归的情况下，其中左边的是凸函数，现在你可以尝试对逻辑回归使用相同的成本函数。如右图这是非凸成本函数不是凸的。这会有许多局部最小值，你可以得到，事实证明对于逻辑回归，那个平方误差成本函数不是一个好的选择。相反，会有一个不同的成本函数可以使成本函数再次凸。梯度下降可以保证收敛到局部最小值。我唯一改变的是我把一半放在总和里面而不是总和外面。为了建立一个新的成本函数，我们将用于逻辑回归，我将稍微改变w和b的定义函数J的定义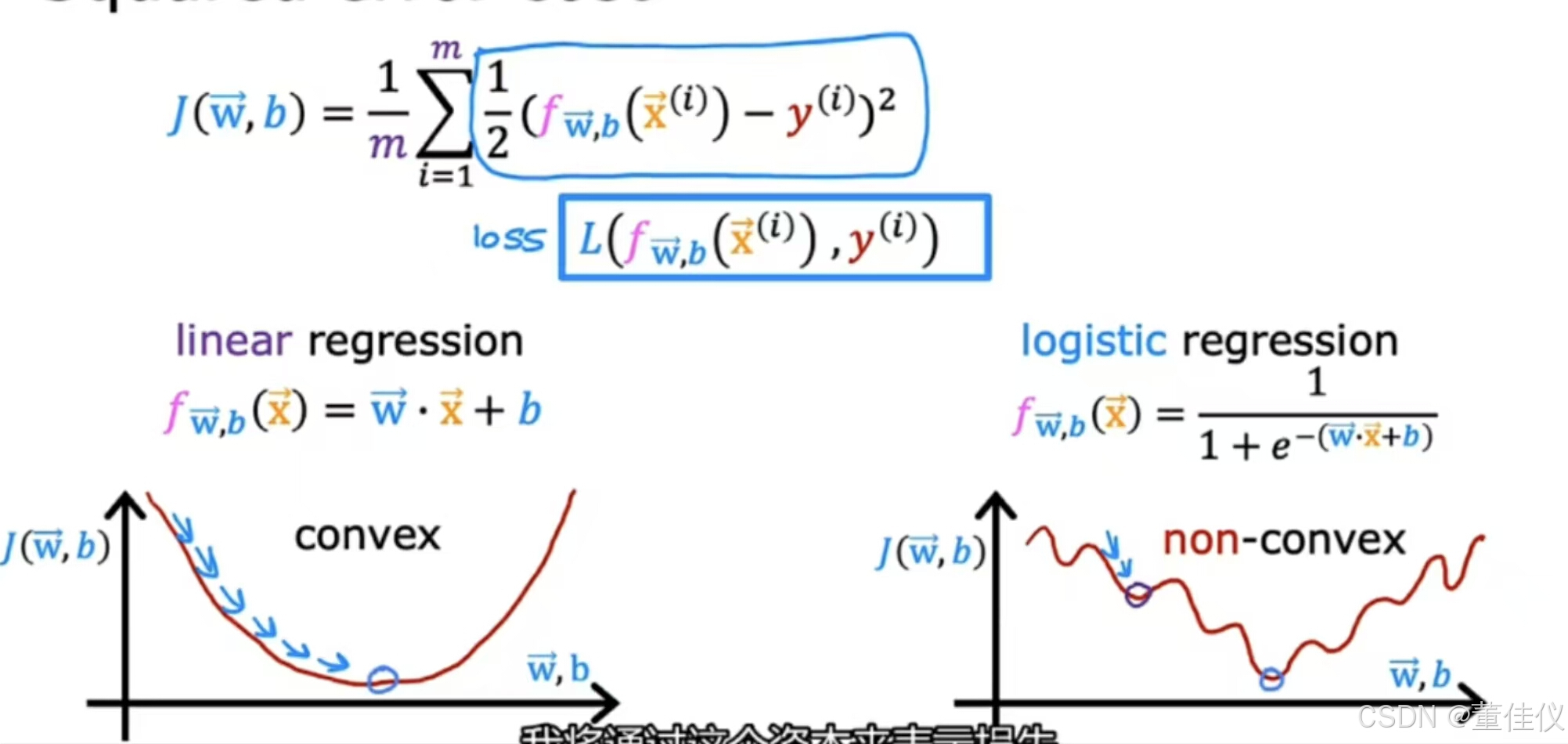我将通过这个资本来表示损失L和作为学习算法预测的函数。在这里只写损失函数的定义，我们将用于逻辑回归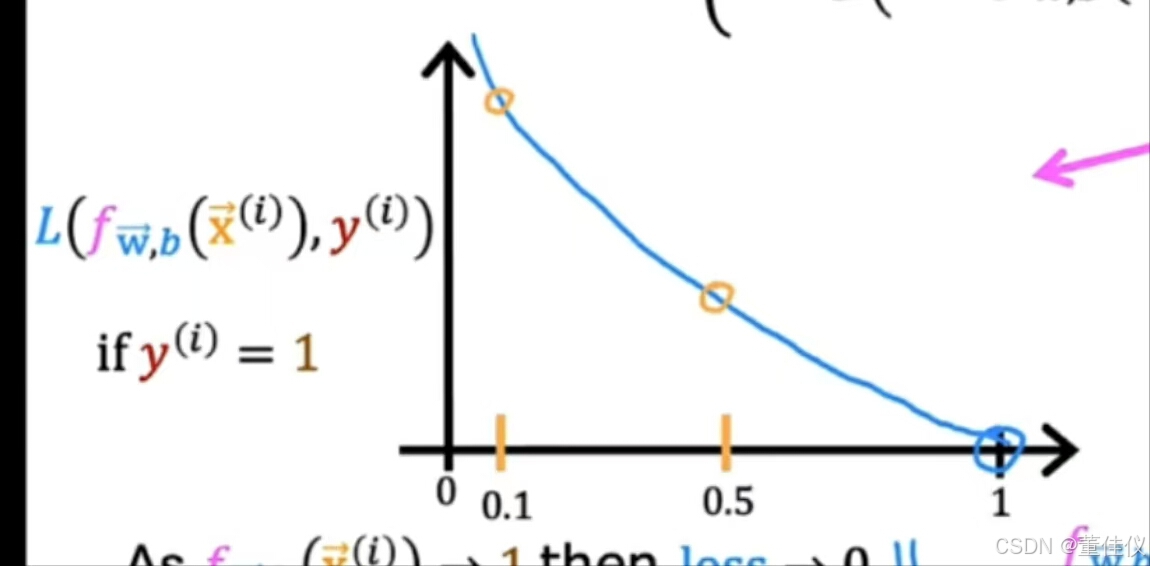，这里横坐标越接近1损失越少，损失越大横坐标越小。在这里，让我们看一下y等于0时对应的损失函数的第二部分绘制此函数时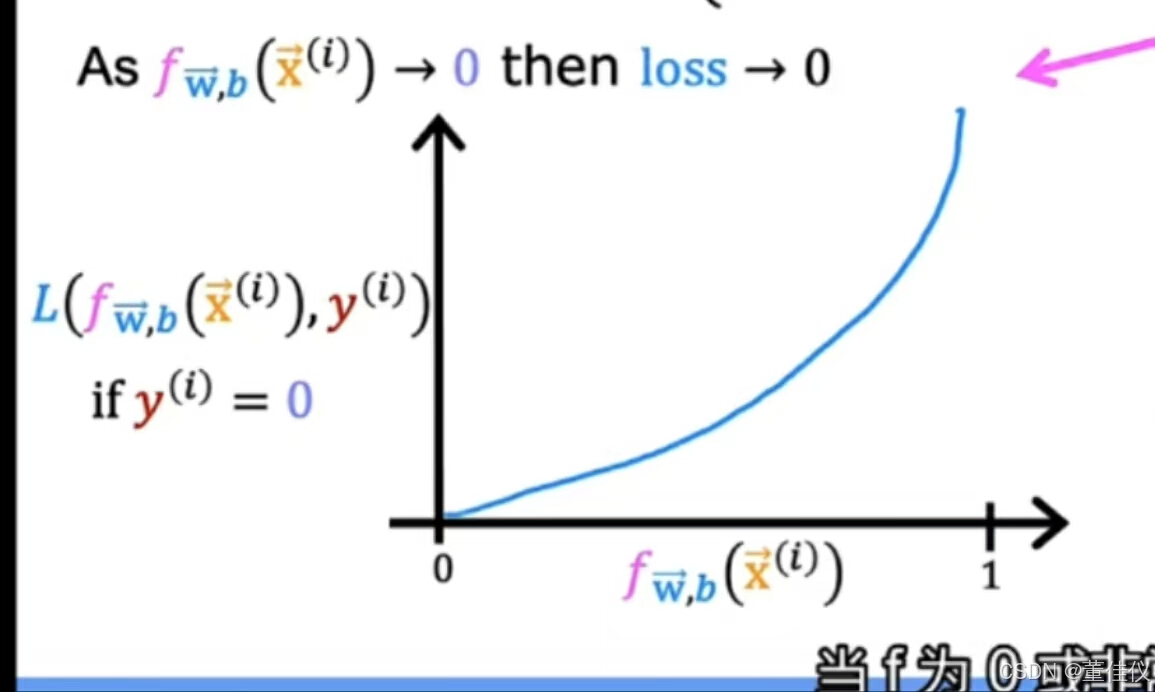，f的范围仅限与0到1，因为逻辑回归仅输出0到1之间的值，当f非常小的时候，损失也非常小，随着预测接近1，损失实际上接近无穷大。