基础算法之背包DP

冰茶几

已于 2024-07-16 15:04:49 修改

阅读量1.1k

点赞数 7

文章标签：算法

于 2024-05-27 23:09:49 首次发布

本文链接：https://blog.csdn.net/DKberry/article/details/139247634

版权

一：0/1背包

有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。

第 $i$ 件物品的体积是 $v_i$ ，价值是 $w_i$ 。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

数据范围
$\lt N, V \le 1000$
$0\lt v_i, w_i \le 1000$
时间复杂度：
$O(n\times m)$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 1e3 + 10;

int n,m;
int f[N],w[N],v[N];

int main(){
    cin>>n>>m;

    rep(i,0,n-1) cin>>v[i]>>w[i];

    rep(i,0,n-1)
        per(j,m,v[i])
            f[j]=max(f[j],f[j-v[i]]+w[i]);
   
    cout<<f[m];
    
    return 0;
}

$\color{BLUE}{这里如果直接采用二维数组对状态进行记录，会出现 MLE。可以考虑改用滚动数组的形式来优化。}$

由于对 $f_i$ 有影响的只有 $f_{i-1}$ ，可以去掉第一维，直接用 $f_{i}$ 来表示处理到当前物品时背包容量为 $i$ 的最大价值，得出以下方程：
$f_j=\max \left(f_j,f_{j-w_i}+v_i\right)$
务必牢记并理解这个转移方程，因为大部分背包问题的转移方程都是在此基础上推导出来的。

$\color{RED}{为什么不能用顺序循环}$

因为j是顺序循环，f[j-v[i]]会先优于f[j]更新，也就是说，用这一层（原本是上一层）的f[j-v[i]]去更新f[j]，会出错，只有拿上一层的f[j-v[i]]去更新f[j]才是正确的

$\color{ORANGE}{DP+贪心(变形)}$
在这里插入图片描述

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = x; i <= y; i++)
#define per(i,x,y) for(int i = x; i >= y; i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define PII pair<int, int>
#define endl '\n'
#define ms(x, n) memset(x,n,sizeof (x));
using ll = long long;
const int N = 5e3 + 10, mod = 998244353;

int n,T;
struct node{
    int t,d,p;
};
node h[N];
int f[N];

bool cmp(node a,node b){
    if(a.d==b.d) return a.p>b.p;
    return a.d<b.d;//不用加else
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin>>T;

    while(T--){
        cin>>n;
        // ms(h,0);
        ms(f,0);
        rep(i,1,n) cin>>h[i].t>>h[i].d>>h[i].p;
        // rep(i,0,N) f[i]=0;

        sort(h+1,h+n+1,cmp);
        
        //f[0]=0;
        rep(i,1,n)
            per(j,h[i].d,h[i].t)
                f[j]=max(f[j],f[j-h[i].t]+h[i].p);

        int res=0;
        rep(i,0,N) res=max(res,f[i]);
        cout<<res<<endl;

    }



    return 0;
}

二：完全背包

有 $N$ 种物品和一个容量是 $V$ 的背包，每种物品都有无限件可用。

第 $i$ 种物品的体积是 $v_i$ ，价值是 $w_i$ 。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

数据范围

$\lt N, V \le 1000$
$\lt v_i, w_i \le 1000$
时间复杂度：
$O (n * m)$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 1e3 + 10;

int n,m;
int f[N],w[N],v[N];

int main(){
    cin>>n>>m;

    rep(i,0,n-1) cin>>v[i]>>w[i];

	//区别
    rep(i,0,n-1)   
        rep(j,v[i],m)
            f[j]=max(f[j],f[j-v[i]]+w[i]);

    cout<<f[m];

    return 0;
}

三：多重背包问题（ $\color{green}{朴素}$ ）

可以先转化为0/1背包问题求解
s是每种物品的最大数量

有 $N$ 种物品和一个容量是 $V$ 的背包。

$\color{red}{\text{第 } i \text{ 种物品最多有 } s_i \text{ 件，每件体积是 } v_i}$ ，价值是 $w_i$ 。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数， $N ， V$ ，用空格隔开，分别表示物品种数和背包容积。

接下来有 $N$ 行，每行三个整数 $v_i, w_i, s_i$ ，用空格隔开，分别表示第 $i$ 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

$\lt N, V \le 100$
$\lt v_i, w_i, s_i \le 100$
时间复杂度：
$\times m \times s)$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 1e3 + 10;

int n,m;
int f[N],w[N],v[N],s[N];

int main(){
    cin>>n>>m;

    rep(i,1,n) cin>>v[i]>>w[i]>>s[i];

    rep(i,1,n)
        per(j,m,v[i])
        //k=0
            for(int k=0;k<=s[i] && k*v[i]<=j;k++)
                f[j]=max(f[j],f[j-v[i]*k]+w[i]*k);

    cout<<f[m];

    return 0;
}

二进制优化

可以先转化为0/1背包问题求解
s是每种物品的最大数量

在这里插入图片描述

数据范围
$\lt N \le 1000$
$\lt V \le 2000$
$\lt v_i, w_i, s_i \le 2000$ ⬆️
时间复杂度：
$O (n * m * l o g (s))$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 2e3 + 10;

int n,m;
int f[N];
//!!!
int ww[N*12],vv[N*12];

int main(){
    cin>>n>>m;

    int num=1;//拆分计数
    rep(i,1,n){
        int v,w,s;
        cin>>v>>w>>s;
        //二进制拆分
        for(int j=1;j<=s;j<<=1){
            vv[num]=j*v;//存体积
            ww[num++]=j*w;//存价值
            s-=j;
        }
        if(s){//剩余
            vv[num]=s*v;
            ww[num++]=s*w;
        }
    }
    
    //0/1背包
    rep(i,1,num)
        per(j,m,vv[i])
            f[j]=max(f[j],f[j-vv[i]]+ww[i]);

    cout<<f[m];

    return 0;
}

单调队列优化

1.因为f[k]通过前面的旧值g[q[h]]来更新，所以窗口在g数组上滚动
2.f[k]=窗口的最大值+还能放入物品的价值
3.队列里存的是下标， $q [h]$ 等于前面最大 $f [j]$ 的下标 $j$ ， $f [j]$ 是剩下空间的容量，那么 $(k - q [h]) / v$ 就是还能放入该物品的个数

数据范围
$\lt N \le 1000$
$\lt V \le 20000$ ⬆️
$\lt v_i, w_i, s_i \le 20000$ ⬆️
时间复杂度：
$\times m)$

内循环控制f[0…m]进出队各一次，次数为 $O (m)$ ，外循环为次数为n

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 2e4 + 10;

int n,m;
int f[N],g[N],q[N];

int main(){
    cin>>n>>m;

    rep(i,0,n-1){
        memcpy(g,f,sizeof f);//f备份到g
        int v,w,s;
        cin>>v>>w>>s;
        //这里不能取j=1
        rep(j,0,v-1){//分拆成v个类
            int hh=0,tt=-1;
            for(int k=j;k<=m;k+=v){//对每一个类使用单调队列
                //q[h]不在窗口 [k - s * v, k - v]内，队头出队
                if(hh<=tt && q[hh]< k-s*v) hh++;
                //使用队头更新最大值
                if(hh<=tt) f[k]=max(f[k],g[q[hh]]+(k-q[hh])/v*w);
                //当前值比队尾值更有价值，队尾出队
                while(hh<=tt && g[k] >= g[q[tt]]+(k-q[tt])/v*w) tt--;
                //下标入队，便于队头出队
                q[++tt]=k;
            }
        }
    }
    cout<<f[m];

    return 0;
}

区别

在这里插入图片描述
两种优化方法都应用了 $\color{red}{拆分思想}$

$\color{blue}{二进制优化}$ 拆分的是 $\color{blue}{物品数量s}$ ，s件拆分成 $l o g s$ 件
$\color{blue}{单调队列优化}$ 拆分的是 $\color{blue}{背包容量m}$ ，根据v的余数，把f[0…m]拆分成v个类，使f[0…M]在 $O (m ）$ 内完成更新

$\color{gold}{学习算法，在于学习算法的演化过程，算法的优化过程，从中体会算法的精妙所在---董老师}$

四：分组背包

有 $N$ 组物品和一个容量是 $V$ 的背包。
每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 $v_{ij}$ ，价值是 $w_{ij}$ ，其中 $i$ 是组号， $j$ 是组内编号。

第一行有两个整数 $N ， V$ ，用空格隔开，分别表示物品组数和背包容量。
接下来有 $N$ 组数据：

每组数据第一行有一个整数 $S_i$ ，表示第 $i$ 个物品组的物品数量；
每组数据接下来有 $S_i$ 行，每行有两个整数 $v_{ij}, w_{ij}$ ，用空格隔开，分别表示第 $i$ 个物品组的第 $j$ 个物品的体积和价值；

输出一个整数，表示最大价值。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

数据范围
$\lt N, V \le 100$
$\lt S_i \le 100$
$\lt v_{ij}, w_{ij} \le 100$
时间复杂度：
$\times m \times S)$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 1e3 + 10;

int n,m;
int f[N];
int v[N][N],w[N][N],s[N];

int main(){
    cin>>n>>m;

    rep(i,0,n-1){
        cin>>s[i];
        rep(j,0,s[i]-1)//!!!
            cin>>v[i][j]>>w[i][j];
    }    
    
    rep(i,0,n-1)
        per(j,m,0)//似0/1，非0/1
            rep(k,0,s[i]-1)//!!!
                if(v[i][k]<=j)
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
    cout<<f[m];


    return 0;
}

（四）背包小结

有1个，有无限个，有多个，每组有多个但每组只能选1个

五：混合背包

结合0-1背包、完全背包和多重背包的混合问题。

第一行两个整数， $N ， V$ ，用空格隔开，分别表示物品种数和背包容积。

接下来有 $N$ 行，每行三个整数 $v_i, w_i, s_i$ ，用空格隔开，分别表示第 $i$ 种物品的体积、价值和数量。

$s_i = -1$ 表示第 $i$ 种物品只能用1次；
$s_i = 0$ 表示第 $i$ 种物品可以用无限次；
$s_i >0$ 表示第 $i$ 种物品可以使用 $s_i$ 次；

输出一个整数，表示最大价值。

数据范围
$\lt N, V \le 1000$
$\lt v_i, w_i \le 1000$
$\le s_i \le 1000$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 1e3 + 10;

int n,m;
int f[N];

int main(){
    cin>>n>>m;

    rep(i,1,n){
        int v,w,s;
        cin>>v>>w>>s;
        if(s==0){
            rep(j,v,m)//!!!
                f[j]=max(f[j],f[j-v]+w);
        }
        else{
            //二进制拆分+0/1背包 -->多重背包
            if(s==-1) s=1;
                for(int k=1;k<=s;k<<=1){
                    per(j,m,v*k)
                        f[j]=max(f[j],f[j-v*k]+w*k);
                        s-=k;
                }
                if(s){
                    per(j,m,s*v)
                        f[j]=max(f[j],f[j-v*s]+w*s);
                }
        }
    }
    cout<<f[m];

    return 0;
}

六：二维费用

每个物品有两种费用（例如重量和体积），在不超过两种费用的限制下，求所能获得的最大价值。
在0/1背包基础上再添加一种消耗的费用

有 $N$ 件物品和一个容量是 $V$ 的背包，背包能承受的最大重量是 $M$ 。
每件物品只能用一次。体积是 $v_i$ ，重量是 $m_i$ ，价值是 $w_i$ 。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

第一行三个整数， $N, V, M$ ，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 $N$ 行，每行三个整数 $v_i, m_i, w_i$ ，用空格隔开，分别表示第 $i$ 件物品的体积、重量和价值。

数据范围
$\lt N \le 1000$
$\lt V, M \le 100$
$\lt v_i, m_i \le 100$
$\lt w_i \le 1000$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 1e3 + 10;

int n,V,M;
int f[N][N];

int main(){
    cin>>n>>V>>M;

    rep(i,1,n){
        int v,w,m;
        cin>>v>>m>>w;
        per(j,V,v)
            per(k,M,m)
                f[j][k]=max(f[j][k],f[j-v][k-m]+w);
    }
    cout<<f[V][M];

    return 0;
}

七：背包问题求最优方案数

在0-1背包问题中，求在不超过最大容量的情况下，所能获得最大价值的方案数。

$\color{red}{什么都不装也算一种方案}$
有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。
第 $i$ 件物品的体积是 $v_i$ ，价值是 $w_i$ 。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出 最优选法的方案数。注意答案可能很大，请输出答案模 $10^9 + 7$ 的结果。

第一行两个整数， $N ， V$ ，用空格隔开，分别表示物品数量和背包容积。
接下来有 $N$ 行，每行两个整数 $v_i, w_i$ ，用空格隔开，分别表示第 $i$ 件物品的体积和价值。

输出一个整数，表示 方案数 模 $10^9 + 7$ 的结果。

数据范围
$\lt N, V \le 1000$
$0\lt v_i, w_i \le 1000$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 1e3 + 10, mod = 1e9+7;

int n,m;
int f[N],g[N];

int main(){
    cin>>n>>m;

    memset(f,-0x3f,sizeof f);// 避免没有装满而进行了转移
    f[0]=0;
    g[0]=1;

    rep(i,1,n){
        int v,w;
        cin>>v>>w;
        per(j,m,v){
            int maxv=max(f[j],f[j-v]+w);
            int cnt=0;
            if(maxv==f[j]) cnt+=g[j];
            if(maxv==f[j-v]+w) cnt+=g[j-v];
            g[j]=cnt%mod;
            f[j]=maxv;
        }
    }

    int res=0;// 寻找最优解
    rep(i,0,m) res=max(res,f[i]);

    int cnt=0;
    rep(i,0,m)
        if(res==f[i])
            cnt=(cnt+g[i])%mod;// 求和最优解方案数
    cout<<cnt;

    return 0;
}

$f_{i,j}$ 表示只考虑前 i 个物品时背包体积「正好」是 $j$ 时的最大价值。
$g_{i,j}$ 表示只考虑前 i 个物品时背包体积「正好」是 $j$ 时的方案数。

八：背包问题求具体方案

有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。
第 $i$ 件物品的体积是 $v_i$ ，价值是 $w_i$ 。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出 字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 $1 \dots N$ 。

输出一行，包含若干个用空格隔开的整数，表示最优解中所选物品的编号序列，且该编号序列的字典序最小。
物品编号范围是 $1 \dots N$ 。

数据范围
$\lt N, V \le 1000$
$0\lt v_i, w_i \le 1000$
时间复杂度：
$\times V)$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
using LL = long long;
const int N = 1e3 + 10;

int f[N][N],w[N],v[N];
int n,m;

int main(){
    cin>>n>>m;

    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i=n;i>=1;i--)
        for(int j=0;j<=m;j++){
            f[i][j]=f[i+1][j];
            if(v[i]<=j) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
    }

    int j=m;
    for(int i=1;i<=n;i++){
        if(v[i]<=j && f[i][j] == f[i+1][j-v[i]]+w[i]){
            cout<<i<<' ';
            j-=v[i];
        }
    }
            

    return 0;
}

九：有依赖的背包问题

物品之间有依赖关系，某个物品被选择的前提是另一个物品必须被选择。(拓扑排序）

有 $N$ 个物品和一个容量是 $V$ 的背包。
物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。
如下图所示：
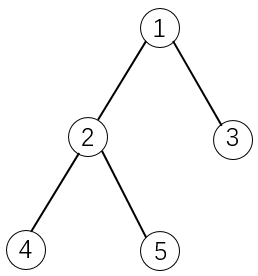
QQ图片20181018170337.png

如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。
每件物品的编号是 $i$ ，体积是 $v_i$ ，价值是 $w_i$ ，依赖的父节点编号是 $p_i$ 。物品的下标范围是 $1 \dots N$ 。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。

第一行有两个整数 $N ， V$ ，用空格隔开，分别表示物品个数和背包容量。
接下来有 $N$ 行数据，每行数据表示一个物品。
第 $i$ 行有三个整数 $v_i, w_i, p_i$ ，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 $p_i = -1$ ，表示根节点。 数据保证所有物品构成一棵树。

数据范围
$\le N, V \le 100$
$\le v_i, w_i\le 100$
父节点编号范围：

内部结点： $\le p_i \le N$ ;
根节点 $p_i = -1$ ;

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define per(i,x,y) for(int i = (x); i >= (y); i--)
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
using ll = long long;
const int N = 1e3 + 10;

int n,m;
int f[N][N],w[N],v[N];
int e[N],ne[N],h[N],idx;

void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u){
    for(int i=h[u];i!=-1;i=ne[i]){// 循环物品数
        int soon=e[i];
        dfs(e[i]);

        per(j,m-v[u],0)// 循环体积
            rep(k,0,j)// 循环策略
                f[u][j]=max(f[u][j],f[u][j-k]+f[soon][k]);
    }
    //将物品u加进去
    per(i,m,v[u]) f[u][i]=f[u][i-v[u]]+w[u];
    //如果当前体积小于根节点，必然放不进去（f=0）
    rep(i,0,v[u]-1) f[u][i]=0;
}


int main(){
    cin>>n>>m;

    memset(h,-1,sizeof h);

    int root;
    rep(i,1,n){
        int p;
        cin>>v[i]>>w[i]>>p;
        if(p==-1) root=i;
        else add(p,i);
    }

    dfs(root);

    cout<<f[root][m];

    return 0;
}

冰茶几

关注

7
点赞
踩
18

收藏

觉得还不错? 一键收藏
0
评论
基础算法之背包DP

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。，用空格隔开，分别表示物品种数和背包容积。种物品的体积、价值和数量。输出一个整数，表示最大价值。，用空格隔开，分别表示第。的背包，每种物品都有。是每种物品的最大数量。是每种物品的最大数量。
复制链接

扫一扫