单因素的方差分析|matlab实例分析

【例】4个工厂生产同一批零件，现从个工厂分别抽取5件产品做检测，测得强度值如下表所示：

	1	2	3	4	5
甲厂	110	112	99	95	100
乙厂	105	108	110	95	112
丙厂	85	95	88	78	98
丁厂	70	90	75	82	80

试分析4个工厂生产的产品，其强度是否有显著差异。（α=0.05）

 

分析：把不同工厂生产的产品分别看做一个变量。检验它们的平均质量是否有明显差异，相当于比较4个变量的均值是否一致。①4个变量均服从正态分布。②每一变量的方差相同。③从4个变量抽取的样本相互独立。采用方差分析法来检验不同工厂生产的产品是否有明显差异。

设第i个变量的均值为μi，假设不同工厂生产的产品无显著差异，那么就要检验如下假设：

H0=μ1+μ2+μ3+μ4

利用Matlab编译以下程序：

clear;clc;
load('X.mat');%导入数据
[p,table,stats]=anova1(X);

 

得以下结果：

• 返回值8.92967e-05<0.05，认为不同工厂生产的产品有显著差异。
• 方差分析表（table）中有6列，第一列声明X中可变化性的来源；第二列显示平方和；第三列显示与每一种可变化有关的自由度；第四列显示第二列数据与第三列数据的比值；第五列显示F统计量数据值，是第四列数据的比值；第六列显示检验的最小显著性概率，即第一列输出参数值。

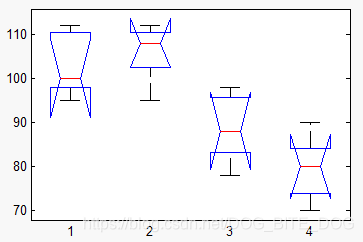
• 从方差分析box图容易看出不同工厂生产的产品之间的直观差异。