2024杭电多校 鸡爪

鸡爪

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 343    Accepted Submission(s): 164

 

Problem Description

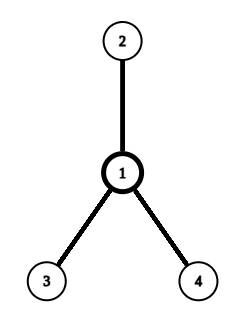
一个鸡爪是由 4 个部分组成，一个点与三个与该点相邻的边，三个边的另一端点被认为**不在**鸡爪中。

一个图上的鸡爪数是该图最多成形成几个鸡爪，使得图上每个点与边最多**在**一个鸡爪中（注意上文点与边是否在鸡爪中的定义）。

现在给你 n 条边，你可以使用任意个点，构造一个简单无向图（没有自环重边），要求最大化该图的鸡爪数，并输出n条边的两端点。如果有多解，请让输出的 2n 个数字在行优先遍历的顺序下，** 字典序最小 **。

字典序：序列A的字典序小于序列B，当且仅当存在i (1≤i≤n)，使得A[i]<B[i]，且对任意的j (1≤j<i)，A[j]=B[j]。

 

Input

第一行为一个整数 T(1≤T≤104) ，表示测试样例个数。

每个样例一行，为一个整数 n(1≤n≤104)。保证所有样例的n的和≤104。

 

Output

每个样例输出 n 行，每行两个正整数，表示该无向边连接的两个顶点（顶点从 1 开始编号）

因为字典序最小所以我们直接跟1 2 3连接

 

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        int m=n/3;
        if(m==0){
            for(int i=2;i<=n+1;i++)
                cout<<1<<' '<<i<<endl;
        }else{
            for(int i=1;i<=min(3,m);i++){
                if(i==1){
                    for(int j=i+1;j<=m+3+(n%3);j++){
                        cout<<i<<" "<<j<<endl;
                    }
                }else{
                    for(int j=i+1;j<=m+4-i;j++){
                        cout<<i<<' '<<j<<endl;
                    }
                }
            }
        }
    }
    return 0;
}