中心极限定理是作为概率论的基础定理,然而很多教科书都没有给出完整证明或引证出处,严重影响到了学习的乐趣。通过在网上查找资料,感谢网友的分享,最终根据傅立叶变换证明该定理,过程很简短,也不要求有太深的数学知识面,下面给出定理的完整证明,首先介绍中心极限定理的定义
中心极限定理:
设随机变量x1,x2,x3…xn相互独立且满足同一分布,则随机变量Yn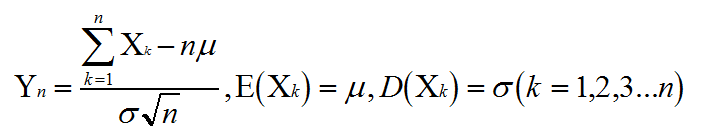
Yn的分布函数Fn(x)
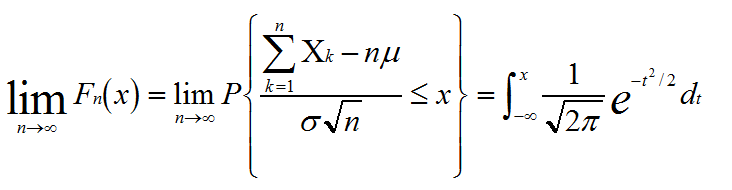
为了证明该定理设(X,Y)是二维连续随机变量,且X,Y相互独立其分布函数分别为:
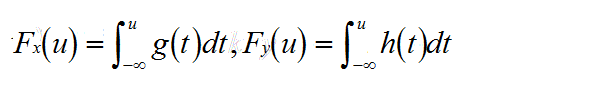
则(X,Y)的概率密度函数f(x,y)=g(x)h(y),若随机变量Z=X+Y,则Z的分布函数Fz(u)=P{Z<=u}=P{X+Y<=u}
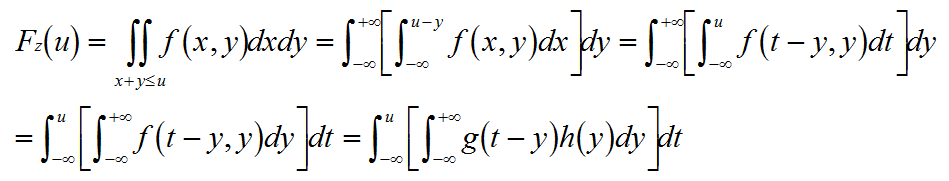
则Z的概率密度fz(u)为
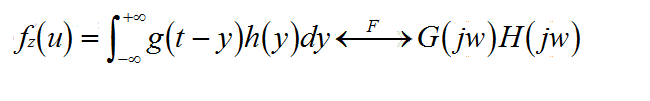
上式有两点结论:1两个独立连续的随机变量的和的概率密度函数是各自概率密度函数的卷积。2由卷积定理知道,和的概率密度函数的傅立叶变换等于各自概率密度函数的傅立叶变换的乘积。
设a,b为实数则(X+b)/a的分布函数为
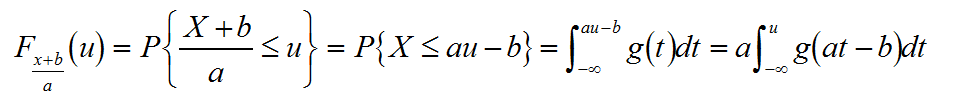
其概率密度以及对应的傅立叶变换为
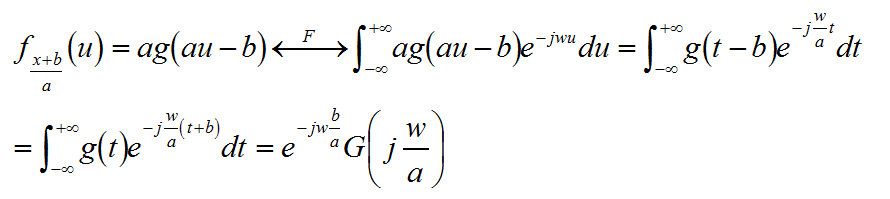
再根据中心极限定理的条件
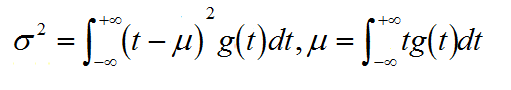
以及Yn
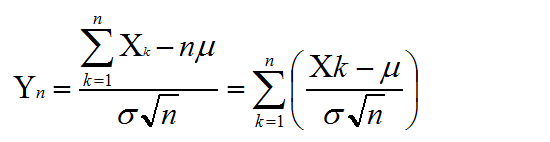
结合前面所得出的结论得到Yn的概率密度及其傅立叶变换
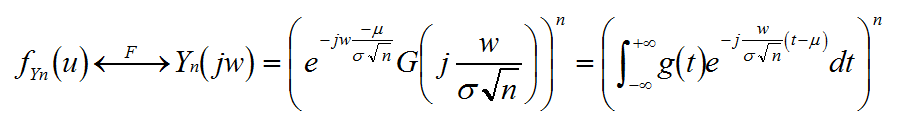
针对上式扩号中的被积函数进行泰勒分解
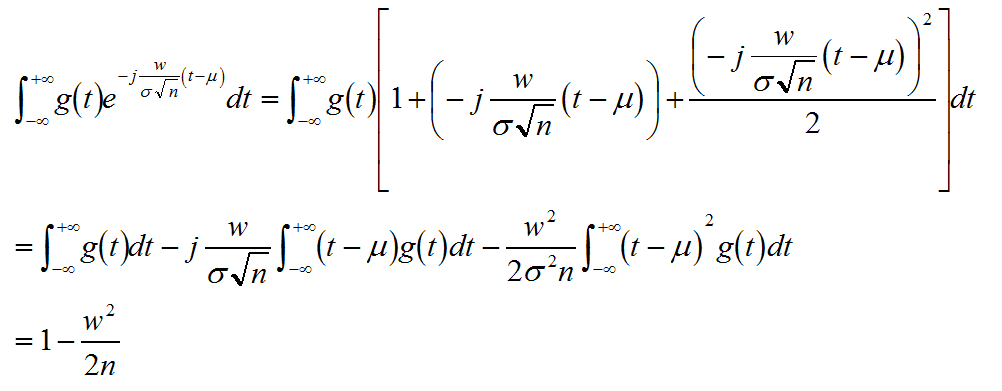
当n趋于无穷,根据傅立叶逆变换求Yn的概率密度
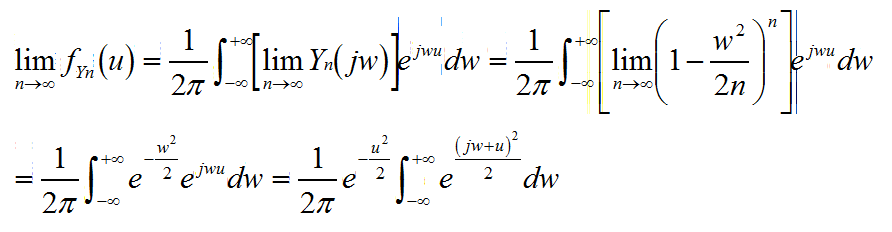
又因为
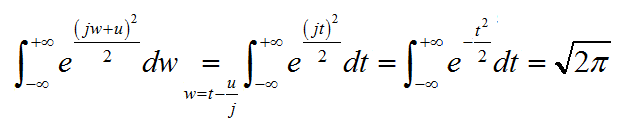
所以得到Yn的概率密度函数
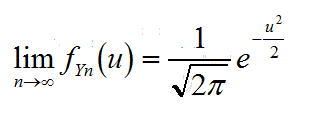
最终得到Yn的分布
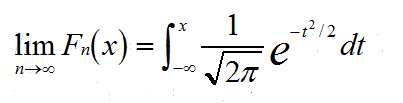
上面的证明非常简短,在学习中心极限定理时确实被它震撼到了,它非常的强大。
中心极限定理的证明
最新推荐文章于 2025-03-22 12:22:19 发布
























 1364
1364

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








