树5 Root of AVL Tree

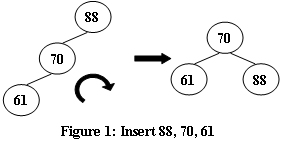
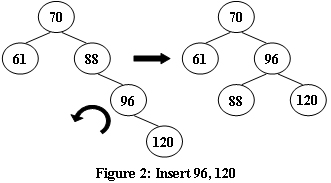
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N$ (≤) which is the total number of keys to be inserted. Then $N$ distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

#include<stdio.h>
#include<stdlib.h>
typedef int ElementType;
typedef struct AVLNode *Position;
typedef Position AVLTree;
struct AVLNode{
	ElementType Data;
	AVLTree Left;
	AVLTree Right;
	int Height;
};


int Max( int a, int b){
	return a>b? a : b;
}


int GetHeight(AVLTree A){  //树的高度，从0开始数
	
	if(A==NULL){
		return -1;
	}
	else{
		int BLHeight = GetHeight(A->Left);
		int BRHeight = GetHeight(A->Right);
		if(BLHeight >= BRHeight) return BLHeight+1;
		else {
			return BRHeight+1;}
	}
}


AVLTree SingleLeftRotation(AVLTree A){
	AVLTree B = A->Left;   //B是A的左子树
	A->Left = B->Right;	    //B的右子树比A小，比B大，挂到A左边
	B->Right = A;    //把A挂到B右边
	A->Height = Max(GetHeight(A->Left),GetHeight(A->Right)) + 1;
	B->Height = Max(GetHeight(B->Left),A->Height) + 1;


	return B;
}


AVLTree SingleRightRotation(AVLTree A){
	AVLTree B = A->Right;
	A->Right = B->Left;
	B->Left = A;
	A->Height = Max(GetHeight(A->Left),GetHeight(A->Right)) + 1;
	B->Height = Max(GetHeight(B->Left),A->Height) +1;


	return B;
}


AVLTree DoubleLeftRightRotation(AVLTree A){
	
	//将B和C做右单旋，返回C
	A->Left = SingleRightRotation(A->Left);
	//A和C左单旋，返回C
	return SingleLeftRotation(A);
}


AVLTree DoubleRightLeftRotation(AVLTree A){


	A->Right = SingleLeftRotation(A->Right);


	return SingleRightRotation(A);
}


AVLTree Insert(AVLTree T, ElementType X){
	if(!T){  //若空树，则新建一个树
		T=(AVLTree)malloc(sizeof(struct AVLNode));
		T->Data = X;
		T->Height = 0;
		T->Left = T->Right = NULL;
	}


	else if(X < T->Data){
		//插入到左子树
		T->Left = Insert(T->Left,X);
		//插入后进行调整，如果需要左旋
		if(GetHeight(T->Left) - GetHeight(T->Right) == 2)
			if(X < T->Left->Data) //如果LL
				T = SingleLeftRotation(T);
			else
				T = DoubleLeftRightRotation(T);
	}


	else if(X > T->Data){
		
		T->Right = Insert(T->Right,X);
		
		if(GetHeight(T->Left) - GetHeight(T->Right) == -2)
			if(X > T->Right->Data)
				T = SingleRightRotation(T);
			else
				T = DoubleRightLeftRotation(T);
	}
	T->Height = Max(GetHeight(T->Left), GetHeight(T->Right)) + 1;
	
	return T;		
	}




int main(){
	int N,temp;
	scanf("%d",&N);
	AVLTree T=NULL;
	for (int i = 0; i < N; ++i)
	{
		scanf("%d",&temp);
		T = Insert(T,temp);
	}
	printf("%d",T->Data );
}

惊叹于LR,RL实现的简洁优雅。