ThreeJS 坐标系转化

这一章主要讲的是屏幕坐标和世界坐标之间的数据转换，在THreeJS中还是非常实用的...

目录

一、什么是屏幕坐标系？

二、什么是世界坐标系？

三、什么是标准化设备坐标系？

四、三个坐标系之间的关系

五、屏幕坐标转世界坐标

六、世界坐标转屏幕坐标 

---

一、什么是屏幕坐标系？

        ThreeJS使用了canvas画布绘制图形，所以屏幕坐标系就是canvas中的坐标系。

屏幕坐标系的起始点在左上角（0，0） 

---

二、什么是世界坐标系？

世界坐标系（三维坐标系）分为两种，左手坐标系和右手坐标系。

• 左手坐标系：BabylonJS
• 右手坐标系：ThreeJS（下图就是右手坐标系）

 

---

三、什么是标准化设备坐标系？

        一旦你的顶点坐标已经在顶点着色器中处理过，它们就应该是标准化设备坐标（Normalized Device Coordinates，NDC）了，标准化设备坐标是一个x、y和z值在-1.0到1.0的一小段空间。任何落在范围外的坐标都会被丢弃/裁剪，不会显示在你的屏幕上。下面你会看到我们定义的在标准化设备坐标中的三角形(忽略z轴)：

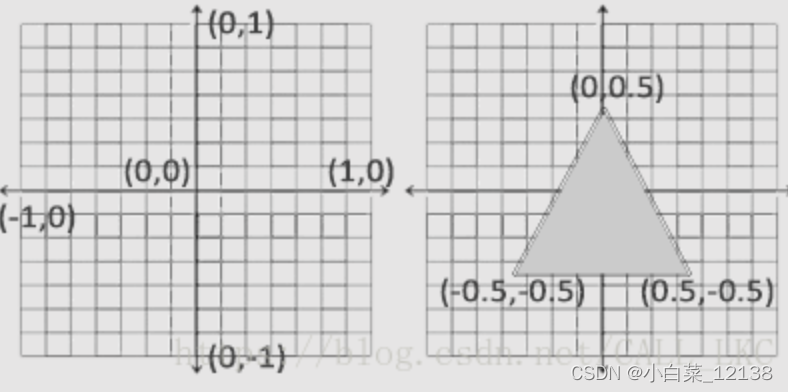
 与通常的屏幕坐标不同，y轴正方向为向上，(0, 0)坐标是这个图像的中心，而不是左上角。最终你希望所有(变换过的)坐标都在这个坐标空间中，否则它们就不可见了。

---

四、三个坐标系之间的关系

        将二维坐标映射到三维空间时，首先需要将二维坐标转换为 NDC 坐标。这可以通过将二维坐标的值除以视口的尺寸来实现。

        一旦获得了 NDC 坐标，可以使用其他投影技术（如透视投影或正交投影）将其转换为三维坐标。

物体坐标系之间的转换关系大致为：

        局部坐标 -> 世界坐标 -> 观察空间坐标 -> 裁剪空间坐标 -> 屏幕空间坐标

        我们将 观察空间坐标系 和 裁剪空间坐标系 之间的转换统一处理，最终得到 标准设备坐标系     

因此坐标转换过程就变成了：

        局部坐标 -> 世界坐标 -> 标准设备坐标 -> 屏幕空间坐标

原本世界坐标转换到观察空间坐标需要乘上视图矩阵 CameraMatrixWorldInverse(ViewMatrix)

  随后，观察空间坐标转换到裁剪空间坐标需要乘上相机投影矩阵：ProjectMatrix

  在 ThreeJS 中有一个方法 Vector3.project(camera) 综合了这两步：
 

project( camera ) {
    return this.applyMatrix4( camera.matrixWorldInverse ).applyMatrix4( camera.projectionMatrix );
}

   

---

五、屏幕坐标转世界坐标

        流程： 屏幕空间坐标 -> 标准设备坐标 -> 世界坐标 

        在ThreeJS 中，画布一般是全屏的，因此画布的宽高 w,h 就是：window.innerWidth 和

window.innerHeight，所以 Three 的空间坐标系中点 (cx, cy)在屏幕坐标系中就是：(w / 2,h / 2)。

        假设 canvas 中有一点 (x,y)，这个点在空间坐标系中为 (x1,y1)，那么这个转换公式是

x1=(x/w)∗2−1

y1=−(y/h)∗2+1

公式推导过程如下：

        1.在屏幕坐标系中，通常将原点放在左上角，x轴向右延伸，y轴向下延伸。这种坐标系的定义方式决定了对于一个点(x, y)，其表示方式是x为横向偏移量，y为纵向偏移量。

        2.当应用原点(cx, cy)后，我们需要计算相对于新的原点的表示方式。对于x'来说，它表示相对于新的原点cx的横向偏移量。因此，我们从原始的x值中减去cx，得到相对于新原点的表示，即x' = x - cx。

        3.同样地，对于y'来说，它表示相对于新的原点cy的纵向偏移量。由于屏幕坐标系中y轴方向与常规的数学坐标系相反，我们需要通过计算cy减去原始的y值，得到相对于新原点的表示，即y' = cy - y。

export function twoConversionThreePlus(event, mesh, raycaster, camera) {
    //raycaster 是new THREE.Raycaster();
    //mesh 是网格，可以是scene
    //camera 是当前的活动相机
    const mouse = new THREE.Vector2(
        (event.clientX / window.innerWidth) * 2 - 1,
        -(event.clientY / window.innerHeight) * 2 + 1
    );

    raycaster.setFromCamera(mouse, camera);
    const intersects = raycaster.intersectObject(mesh, true);
    if (intersects.length <= 0) return void 0;
    const selected = intersects[0].object;

    console.log(intersects[0].point, "===", selected);

    return intersects[0].point;
}

//当前函数将返回mesh上点的三维坐标（由鼠标指针指向的点）

---

六、世界坐标转屏幕坐标 

        流程：世界坐标 -> 标准设备坐标 -> 屏幕空间坐标

        通过 Vector3对象的方法 project(camera)，返回的结果是世界坐标 worldVector在 camera相机对象矩阵变化下对应的标准设备坐标， 标准设备坐标 xyz 的范围是[-1,1]。

        同样的，假设画布宽为 w ，高为 h，屏幕坐标系中的一点为 (x, y)，标准设备坐标系中对应的点为 (x1, y1)

        从标准设备坐标系转换到屏幕坐标系与我们前面计算出的公式相反：

x = x1 * w/2 + w/2

y = y1 * h/2 + h/2

export function threeConversionTwo(model, camera) {
    // 这里判断model是因为model可能是被选中的mesh的position，也可能是点击到了环境贴图
    if (model !== undefined) {
        // 世界坐标转标准设备坐标
        const worldVectorsss = new THREE.Vector3(model.x, model.y, model.z)
        const stdVectorsss = worldVectorsss.project(camera);
        console.log(stdVectorsss)

        const a = window.innerWidth / 2;
        const b = window.innerHeight / 2;
        //标准设备坐标转屏幕坐标x,y
        const x = Math.round(stdVectorsss.x * a + a);
        const y = Math.round(-stdVectorsss.y * b + b);

        console.log(x, y)
    }
    return
}