实验方法探讨标准正态分布随机数发生器

 

一般的程序设计语言都会提供U(0,1)的伪随机数生成函数/类，但如果想得到的是服从标准正态分布的随机数又应该怎样做呢？《Numerical Recipes in C++ 2/e》已经给出了详尽的解答，这里先引用一篇网上的文章，以引出问题：

 -----------------------------------------------------------------------------
正态分布的随机数发生器 in C#
Trackback: http://tb.blog.csdn.net/TrackBack.aspx?PostId=178666
-----------------------------------------------------------------------------

主要参考《Numerical Recipes in C++ 2/e》p.292～p.294 和《Simulation Modeling and Analysis 3/e》p.465～p.466。

Box 和 Muller 在 1958 年给出了由均匀分布的随机变量生成正态分布的随机变量的算法。设 U1, U2 是区间 (0, 1) 上均匀分布的随机变量，且相互独立。令

X1 = sqrt(-2*log(U1)) * cos(2*PI*U2);
X2 = sqrt(-2*log(U1)) * sin(2*PI*U2);

那么 X1, X2 服从 N(0,1) 分布，且相互独立。等于说我们用两个独立的 U(0,1) 随机数得到了两个独立的 N(0,1)随机数。

Marsaglia 和 Bray 在 1964 年提出了一种改进算法，避免使用三角函数。以下的实现代码用的就是这种改进算法。

     public   class  GaussianRNG
     ... {
        int iset;
        double gset;
        Random r1, r2;

        public GaussianRNG()
        ...{
            r1 = new Random(unchecked((int)DateTime.Now.Ticks));
            r2 = new Random(~unchecked((int)DateTime.Now.Ticks));
            iset = 0;
        }

        public double Next()
        ...{
            double fac, rsq, v1, v2;
            if (iset == 0)
            ...{
                do
                ...{
                    v1 = 2.0 * r1.NextDouble() - 1.0;
                    v2 = 2.0 * r2.NextDouble() - 1.0;
                    rsq = v1 * v1 + v2 * v2;
                } while (rsq >= 1.0 || rsq == 0.0);

                fac = Math.Sqrt(-2.0 * Math.Log(rsq) / rsq);
                gset = v1 * fac;
                iset = 1;
                return v2 * fac;
            }
            else
            ...{
                iset = 0;
                return gset;
            }
        }
    }

---------------------------------------------------------

看完这段文档，不由得要提出一个问题，为什么算法要同时给出两个服从标准正态分布的随机变量呢？特别是C#代码中，程序保存了一个状态开关，以在被调用时交替输出两个随机变量。这又是为何呢？

《Numerical Recipes in C++ 2/e》对于我等半途出家之辈或曰过于艰辛，还是先把数学上的严谨解释放到一边，用实验的方法说明问题。

考虑如下实践：如果把“正态分布随机数发生器”的这个类放在ASP.net下，以服务器端控件调用Next方法；抑或是将之设为WebService并把Next方法暴露出来，那么对于无状态的环境如何保持iset和gset这两个变量呢？

当然，在无状态环境下保存上下文有很多办法，比如使用Session。但本文想阐述的是，能不能简化程序，使之成为一个无状态的程序呢？首先能想到的去除状态的方法就是删掉iset开关和gset，每次调用都返回v1*fac，但这样处理之后，返回的变量还是服从标准正态分布的吗？从逻辑推理上讲，如果这样处理后依然服从标准正态分布，那么《Numerical Recipes in C++ 2/e》一书恐怕早就改写了吧？因此，处理后所得结果必然不服从标准正态分布。（至于“额外偏离”到底是什么我想就不用知道了吧？）

但是去掉状态后的程序输出的结果是怎样的呢？本文通过数学实验的方法进行测试（以下代码用Mathematice5编写）：

用Mathematica函数移植原算法如下：（GRN：Gaussian Random Number generator）
i = 0;(*开关量, 文中的iset*)
g = 0;(*文中的gset*)
GRN[] := Module[{rsq = 2, v1, v2, fac},
    If[i == 0,
      SeedRandom[];(*then, 初始化随机种子*)
      While[rsq ≥ 1 || rsq == 0,
        v1 = Random[Real, {-1, 1}];
        v2 = Random[Real, {-1, 1}];
        rsq = v1*v1 + v2*v2;
        ];
      fac = Sqrt[-2*Log[rsq]/rsq];
      g = v1*fac;
      i = 1;
      v2*fac,(*else*)
      i = 0;
      g
      ]
    ]

改写成无状态的函数如下：（GRNNS：GRN within No Status）
GRNNS[] := Module[{rsq = 2, v1, v2, fac},
    SeedRandom[];
    While[rsq ≥ 1 || rsq == 0,
      v1 = Random[Real, {-1, 1}];
      v2 = Random[Real, {-1, 1}];
      rsq = v1*v1 + v2*v2;
      ];
    fac = Sqrt[-2*Log[rsq]/rsq];
    v1*fac
    ]

最后，由主控函数生成样本，并绘制直方图：
<< Statistics`DataManipulation` (*引入外部插件*)
<< Graphics`Graphics`
n = 10000;(*样本容量*)
t1 = Table[GRN[], {n}];
t2 = BinCounts[t1, {-3, 3, 0.1}];(*做3σ内的已0.1为步长的区域统计*)
t3 = t2/n;(*标准化*)
f1 = Table[GRNNS[], {n}];
f2 = BinCounts[f1, {-3, 3, 0.1}];
f3 = f2/n;
BarChart[t3, f3];(*画柱形图*)
Mean[t1](*样本均值*)
Variance[t1](*样本方差（无偏估计）*)
Mean[f1]
Variance[f1]

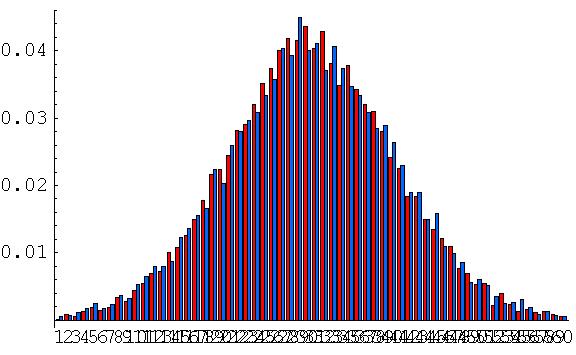
可得到直方图：

其中红线为原算法，蓝线为去掉状态的算法。

以及统计量：
GRN样本均值=0.00509731
GRN样本方差=0.965504

GRNNS样本均值=-0.00212686
GRNNS样本方差=1.00834

且比较多次实验结果，虽有波动，但基本水平稳定。

可以看到，去掉状态后算法的表现与原来相差无几。

结论：
虽然去掉状态后的发生器产生的随机序列应该不服从标准正态分布，但出于简化应用等的考虑可以去除状态。并且在去除状态后，得到的总体与原算法差别不大。

Future：
希望能够尽快从数值分析理论中得到解释，作为本人第一篇博客文章，还望各位指教。