机械臂之贝塞尔曲线的应用

作者：岁聿云暮

前言

这篇是自制机械臂项目的运行姿态优化。想尝试做一个机械臂的可以参考这篇文章: 《如何做个机械臂》。

尝试使用MarsCode来辅助编程，挺好用的，能提升效率。

缘由

目前机械臂只会固定某个速度从开始位置旋转到目标位置，看起来多少有点僵硬。故想着如何让机械臂运行起来更加自然，举个例子，可以想象一下扇扇子的动作，慢 -> 快 -> 慢。那如何解决这个问题，我第一时间想到的是贝塞尔曲线。就像css的css的缓动函数。

目标

机械臂能变速旋转。

先看结果

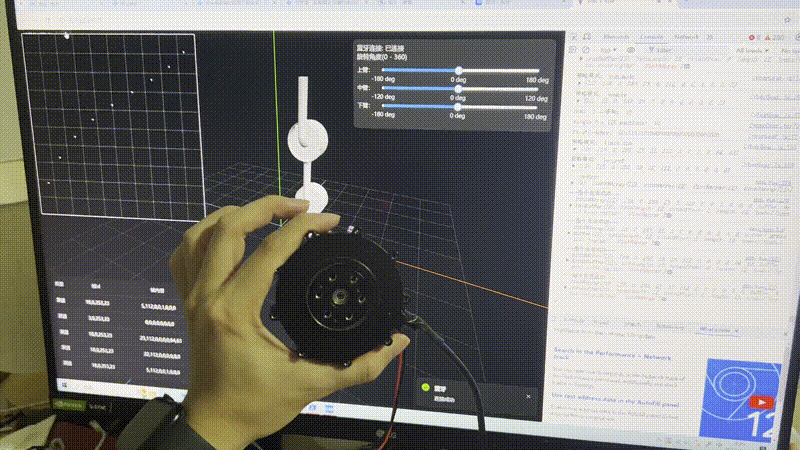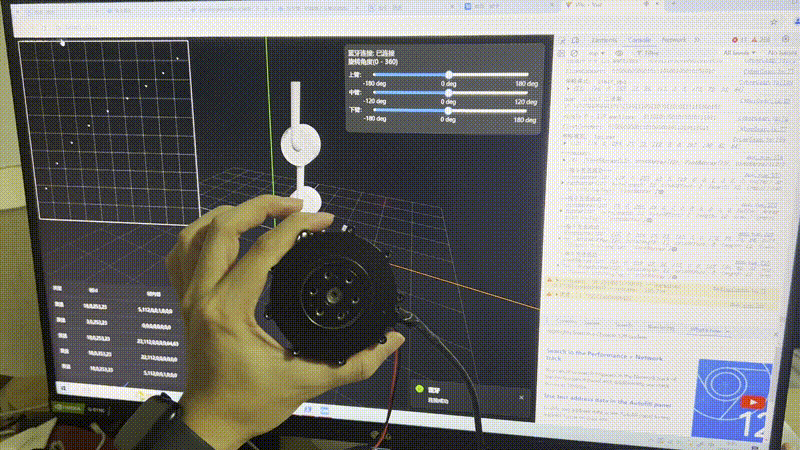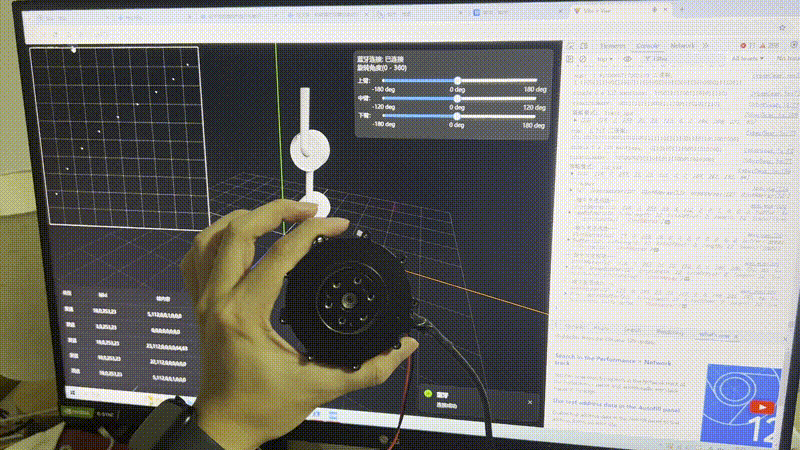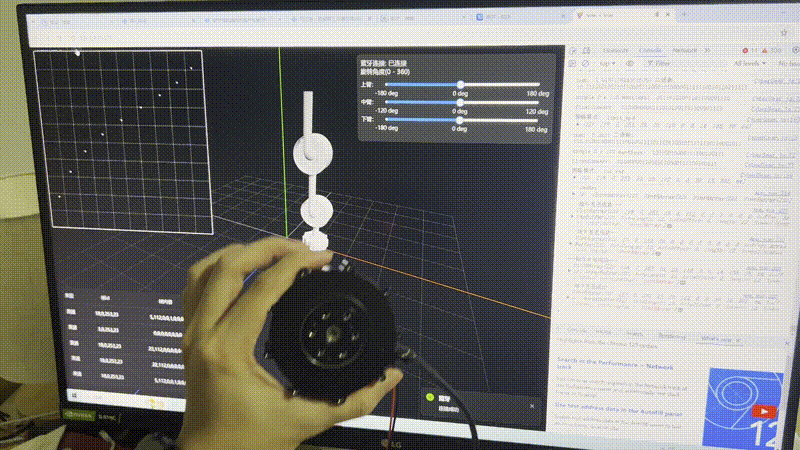
解决过程

由于小米电机的几种控制模式都不支持变速运动。只能从网页端（上位机）层面或单片机层面来做，将原来的匀速距离旋转切分成多段的匀速运动，有点微积分的味道。写c语言有点太累，所以就从网页端来做，理论上蓝牙的传输速率比can快，所以在网页端来做完全没问题。但是，多了一步操作，系统可靠性会降低些。

尝试让豆包MarsCode生成想要的三阶贝塞尔曲线函数：

很完美，写个渲染贝塞尔曲线图的函数，将同等间隔的一百个点渲染到canvas上：

export function drawBezierCurve(p1, p2) {
  // cubic-bezier(.17,.67,.83,.67)
  p1 = [.17,.67];
  p2 = [.83,.67];

  // 创建canvas元素
  var canvas = document.createElement("canvas");
  canvas.id = "myCanvas";
  canvas.width = 500;
  canvas.height = 500;
  canvas.style.backgroundColor = "black";
  canvas.style.border = "1px solid #FFF";
  canvas.style.position = "absolute";
  canvas.style.left = "0";
  canvas.style.top = "0";

  let body = document.querySelector("body");
  body.appendChild(canvas);


  var ctx = canvas.getContext("2d");

  for(let i = 0; i <= 100; i++ ){
    let coordinate = bezierCurve(p1, p2, i / 100);
    // console.log('coordinate: ', coordinate);
    drawPoint(coordinate[0] * 500, (1 - coordinate[1]) * 500 , ctx);
  }

  function drawPoint(x, y, ctx) {
    //  绘制背景为白色的圆
    ctx.beginPath();
    ctx.arc(x, y, 2, 0, 2 * Math.PI);
    ctx.fillStyle = "white";
    ctx.fill();
    ctx.closePath();
  }
}

canvas渲染 如下图：

到此我有个疑问，为什么按时间等分计算，但渲染到图里的点却并不是等分。查询了些文档，比如这篇如何理解并应用贝塞尔曲线 (上图ai中也给了解答：在时间t时贝塞尔曲线上的点)，在此我的理解是：这个函数只是计算出贝塞尔曲线的离散点，这个点代表了具体某个时间（x轴），应当要运动到路程的百分之几（y轴）。

实际验证：
为了简化问题，下面渲染个只有10个点的的贝塞尔曲线图（cubic-bezier(.17,.67,.83,.67)）：

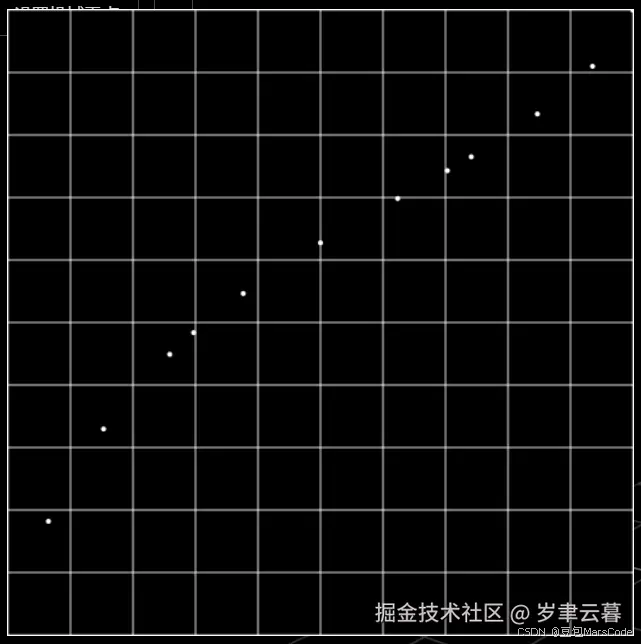
x轴是时间，y轴代表进度。那么可以明确以下观点：
① 不管前面如何运动，只要运行到最后一个点，那么就是运动到终点，即目标位置。
② 区间运动的速度等于 区间的运动距离 / 区间的运动时间，即 v = (y1 - y0) / (x1 - x0) = Δy / Δx

在此还需考虑一些实际问题，比如我设置的蓝牙传输间隔时间为15ms，can消息发送频率等。因为过快的发送蓝牙消息可能会导致消息阻塞，从而影响电机旋转的准确性。

粗略计算一下电机每秒的速度可变化的次数: 三个电机同时运行，电机每次的位置模式需要发四条指令。每秒可以发送蓝牙消息数量： 1000ms / 15ms(蓝牙间隔) = 66条指令。每秒速度的可变次数： 66 / （3 * 4） ≈ 5次。如果之后还要加电机，速度的每秒可变次数会更少。当然可以优化代码，比如将四条指令塞到一条蓝牙消息中（这个等之后做关键帧动画时再优化）。

造轮子时刻：

/**
 * @description: 获取贝塞尔曲线的状态数据列表
 * @param { Array<number> } p1 e.g: [0, 0]
 * @param { Array<number> } p2 e.g: [1, 1]
 * @param { number } count 坐标点的个数
 * @returns { Array<object> } e.g: [{speed: 0.5, rotate: 0.5, duration: 0.5}]
 */
function getCubicCoords(p1, p2, count) {
  let preCoord = [0, 0];
  let cubicCoordData = [];

  for (let i = 1; i <= count; i++) {
    let t = i / count;
    let coordinate = bezierCurve(p1, p2, t);

    // drawPoint(coordinate[0] * 500, (1 - coordinate[1]) * 500, ctx);

    cubicCoordData.push({
      speed: (coordinate[1] - preCoord[1]) / (coordinate[0] - preCoord[0]),
      rotate: coordinate[1],
      duration: preCoord[0],
    });

    preCoord = coordinate;
  }

  return cubicCoordData;
}

getCubicCoords函数得到的是所有离散点所处位置时的速度，旋转角度和经历时间，但这只是百分比，具体还要乘以具体的角度和时间，并生成指令通过蓝牙发送出去：

/**
 * @description 获取一个贝塞尔曲线区间的指令列表，包含 旋转角度，延迟时间，速度
 * @param { object {p1: Array<number>, p2: Array<number>} } cubicBezier
 * @param { number } rotateDeg
 * @param { number } deration
 * @param { motorId } debugger
 * @param { function } sendBleMsg
 */
// export function getCmdSeries(cubicBezier = {p1: [.9,.13], p2: [.88,.28]}, rotateDeg, duration, motorId = 21, sendBleMsg) {
export function getCmdSeries({
    cubicBezier= { p1: [0.9, 0.13], p2: [0.88, 0.28]},
    rotateDeg,
    duration,
    motorId,
    sendBleMsg,
    baseRotate = 0, // 从某个角度开始
  }) {

  let cubicCoordData = getCubicCoordsState(cubicBezier.p1, cubicBezier.p2, 3);
  let avgSpeed = rotateDeg / duration;

  cubicCoordData.forEach(item => {
    let speed = item.speed * avgSpeed;
    let time = item.duration * duration;
    let rotate = item.rotate * rotateDeg;

    setTimeout(() => {
      console.warn('---speed: ', speed, '---duration: ', time, '---rotate: ', rotate);
      sendBleMsg({ motorId: motorId, limit_spd: speed, loc_ref: baseRotate + rotate });
    }, time * 1000);

  });

}

调用下函数，测试两秒钟机械臂旋转一周的表现:

  getCmdSeries({
    cubicBezier: {p1: [.17,.67], p2: [.83,.67]},
    rotateDeg: 360,
    duration: 3,
    motorId: 23,
    sendBleMsg: rotateMotor,
    baseRotate: 0, // 从某个角度开始
  });

结果如下：

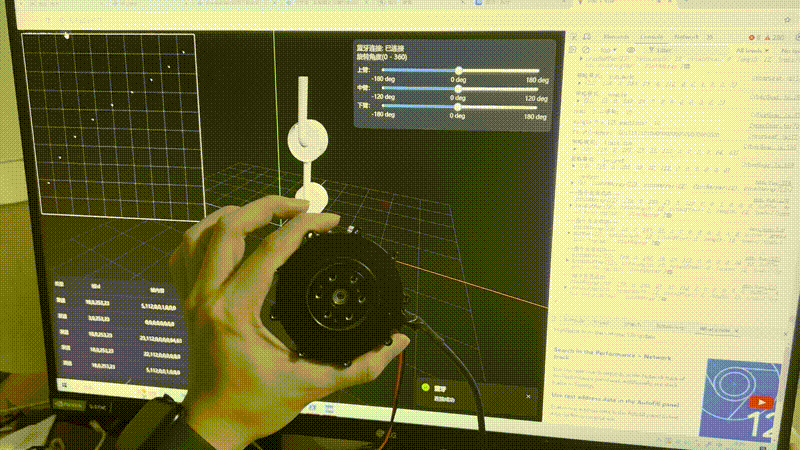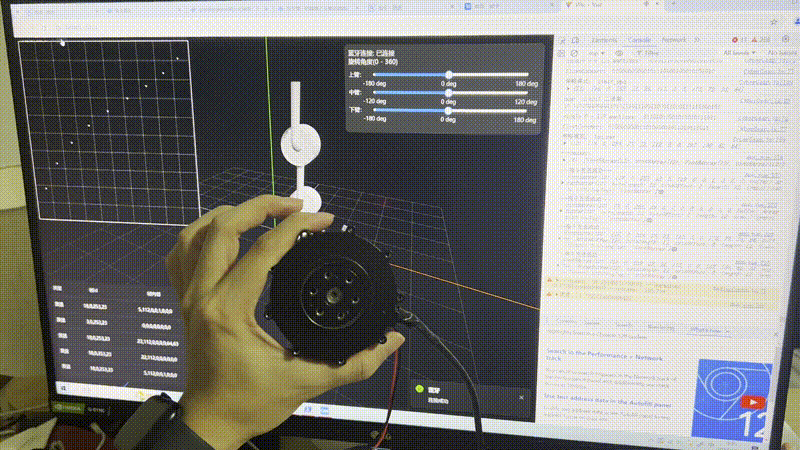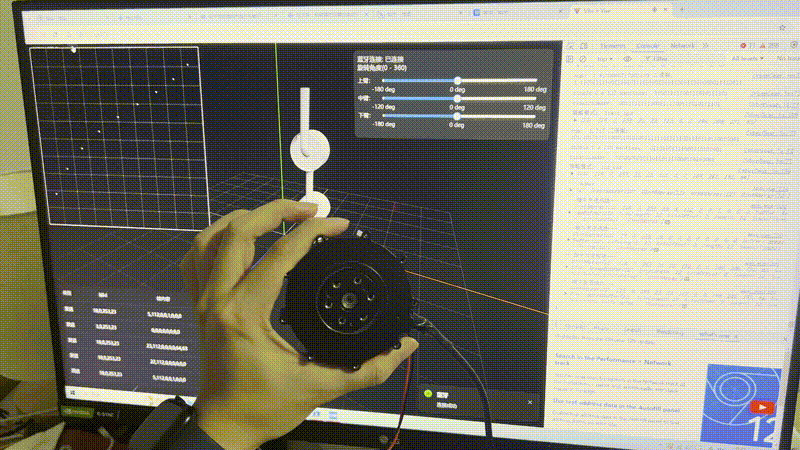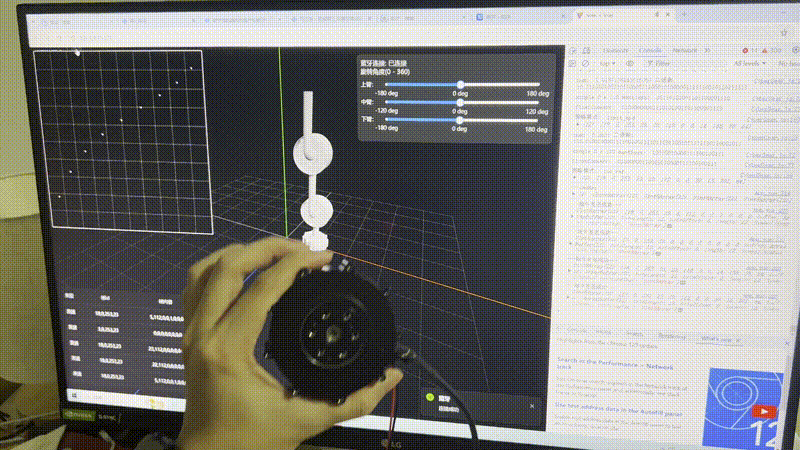
待优化问题

速度切换时会有卡顿的感觉，就是一个区间的速度降到零，然后再提升到下一个区间的速度。理想的速度切换应该是平滑的。