简介:贝塞尔曲线是一种在计算机图形学中被广泛使用的参数曲线,由法国工程师皮埃尔·贝塞尔提出。它在设计、动画、游戏开发和路径规划等多领域有着重要应用。通过控制点定义形状,贝塞尔曲线可通过阶数不同的多项式表示,并通过De Casteljau算法简化计算。在JavaScript环境中,使用贝塞尔曲线可以创建动态效果,并且贝塞尔曲线的源代码包可能包含必要的实现文件。掌握贝塞尔曲线对于数字艺术和软件开发都具有重要价值。 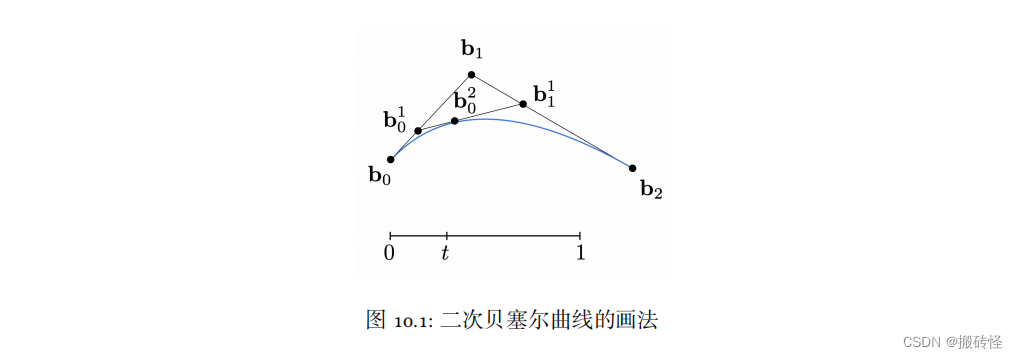
1. Bezier曲线简介与特点
Bezier曲线是计算机图形学中应用广泛的参数曲线,由法国工程师Pierre Bézier首先提出并广泛应用于CAD、动画、游戏开发等领域。这种曲线主要特点在于通过控制点定义曲线形状,具有直观易用、光滑连续等优势。在动画和游戏开发中,Bezier曲线允许设计师精确地控制物体的移动路径,实现平滑无闪烁的动画效果。此外,由于其数学特性,Bezier曲线在计算机动画中的路径规划、交互设计等环节中有着不可替代的作用。在本章中,我们将初步了解Bezier曲线的基本概念,并探讨其在现代IT行业中的重要作用。
2. Bezier曲线的数学基础
2.1 贝塞尔曲线的数学描述
2.1.1 参数方程的形式
贝塞尔曲线的数学表达是一种参数方程形式,它使用控制点来定义曲线的形状。对于一个n阶贝塞尔曲线,其参数方程可以表示为:
B(t) = Σ [n choose i] * (1 - t)^(n-i) * t^i * P_i,其中 i = 0 to n
其中,P_i 表示控制点坐标,t 是一个在0到1之间变化的参数,而[n choose i]表示组合数,也就是从n个不同元素中取i个元素的组合数。
例如,对于一个二次贝塞尔曲线,其方程可以简化为:
B(t) = (1 - t)^2 * P0 + 2t(1 - t) * P1 + t^2 * P2
在这个方程中,P0、P1和P2是三个控制点,它们定义了曲线的大致路径。
2.1.2 各阶贝塞尔曲线的特点
不同阶数的贝塞尔曲线有不同的特性:
- 一阶贝塞尔曲线:由两个控制点定义,是一条直线段。
- 二阶贝塞尔曲线:由三个控制点定义,曲线经过起点和终点,并且由中点控制曲线的方向。
- 三阶贝塞尔曲线:由四个控制点定义,曲线不再仅由两端点控制,而是由所有控制点共同决定。
- 四阶及以上贝塞尔曲线:更复杂,能表示更为复杂的曲线形状。
2.2 贝塞尔曲线的控制点
2.2.1 控制点的作用与影响
控制点是定义贝塞尔曲线形状的核心元素,它们决定了曲线的基本形态和走向。控制点越多,曲线可以描述的形状越复杂。控制点的位置变化直接影响到曲线的弯曲程度和方向。
- 当所有控制点共线时,贝塞尔曲线将是一条直线。
- 当曲线外侧的控制点相对于内部点位置移动时,曲线将向该方向弯曲。
- 如果控制点被移动到曲线外部,贝塞尔曲线会在该点产生尖点或转折点。
2.2.2 控制点与曲线形状的关系
贝塞尔曲线的形状随着控制点的变化而变化,是一种直观而富有弹性的设计工具。在实际应用中,我们可以用以下规则来理解和控制贝塞尔曲线的形状:
- 曲线总是从第一个控制点开始,在最后一个控制点结束。
- 当曲线接近某个控制点时,该控制点会对曲线产生较强的吸引力。
- 控制点之间的连线大致反映了曲线的弯曲程度。
对于高级用户而言,通过调整控制点的位置,可以实现更加精细的曲线设计。例如,在设计复杂字符的笔画路径时,每个控制点都可以根据需要进行精确调整,以达到最佳的视觉效果。
3. De Casteljau算法原理
3.1 De Casteljau算法的几何构造
3.1.1 算法步骤详解
De Casteljau算法是一种稳定且直观的方法,用于构造贝塞尔曲线。算法基于递归思想,通过线性插值构造出贝塞尔曲线的点。以下是De Casteljau算法的具体步骤:
-
初始化 :确定控制点集合,这些控制点定义了贝塞尔曲线的形状。对于一个n阶贝塞尔曲线,需要n+1个控制点。
-
逐层插值 :从控制点集合开始,执行以下操作:
- 对于集合中的每对相邻控制点,计算它们之间的中点,并用这两点连线上的中点来代替这对控制点。例如,对于点P0和P1,它们的中点M01将取代它们。
- 当这个操作完成时,你将得到一个包含n个新点的集合。
-
如果集合中只剩下一个点,则这个点就是贝塞尔曲线上的点。
-
递归 :重复上述的逐层插值过程,直到集合中只剩下一个点。这个点就是曲线上的点。
3.1.2 算法的稳定性分析
De Casteljau算法的一个显著特点是它在数值上的稳定性。由于算法仅使用线性插值,它避免了贝塞尔曲线的数值不稳定问题,例如溢出和舍入误差。线性插值涉及除以常数(通常为2),这是一个稳定的操作。
De Casteljau算法的另一个优势是能够使用仿射变换而不改变曲线的形状,这对于计算机图形学非常重要,因为它允许在不改变曲线形状的情况下进行变换,如平移、旋转和缩放。
3.2 De Casteljau算法的计算过程
3.2.1 线性插值与递归
线性插值是De Casteljau算法的核心步骤之一。对于一对点P0和P1,其线性插值公式为:
L(t) = (1 - t) * P0 + t * P1
其中 t 是参数, t 的范围通常是从0到1。对于贝塞尔曲线,我们通常需要对所有控制点执行多次线性插值。
递归过程如下:
- 对于初始控制点集合{P0, P1, ..., Pn},计算线性插值点集合。
- 对新的点集合重复上述步骤,直到最后只剩下一个点。
3.2.2 实际应用中的算法优化
De Casteljau算法虽然稳定,但在计算过程中可能会比较耗时,特别是对于高阶曲线。为了优化性能,可以考虑以下策略:
-
缓存中间结果 :在递归过程中,计算的许多中间点在后续步骤中可能被重复使用,因此可以将这些中间点存储起来以供后续使用。
-
使用De Boor算法 :对于递归De Casteljau算法,可以采用De Boor算法,这是一种基于差商的迭代版本,能够减少计算量。
-
提前终止条件 :在某些情况下,如果计算的曲线精度已经满足要求,则可以提前终止递归过程,从而节省计算资源。
// 示例代码块:使用JavaScript实现De Casteljau算法的基础步骤
function deCasteljau(controlPoints, t) {
let points = controlPoints.slice();
while (points.length > 1) {
const newPoints = [];
for (let i = 0; i < points.length - 1; i++) {
const point = lerp(points[i], points[i + 1], t);
newPoints.push(point);
}
points = newPoints;
}
return points[0];
}
// Linear interpolation function
function lerp(p0, p1, t) {
return p0.map((value, index) => value + t * (p1[index] - value));
}
// 控制点数组
const controlPoints = [/* 控制点坐标数组 */];
const t = 0.5; // 参数值
// 计算结果
const result = deCasteljau(controlPoints, t);
在上述代码中, deCasteljau 函数实现了De Casteljau算法的基本递归逻辑。我们首先复制控制点数组,然后在循环中对每一对相邻控制点进行线性插值,并用得到的新点数组替换旧数组,直到只剩下一个点。 lerp 函数用于计算两点之间的线性插值。这种实现方式展示了算法的逻辑结构,同时通过逐行注释提供参数和逻辑的详细解释。
以上内容展示了De Casteljau算法的几何构造原理及其计算过程,深入解析了算法的每个步骤,并通过实际代码示例,为理解算法提供了一个具体且实践性的视角。
4. JavaScript实现Bezier曲线
JavaScript作为前端开发的核心技术之一,与HTML5 Canvas的结合为Web应用提供了强大的图形绘制能力。Bezier曲线作为计算机图形学中常见的一种参数曲线,因其简洁的数学描述和易于控制的特性,在Web中有着广泛的应用。本章将重点介绍如何使用JavaScript在HTML5 Canvas上绘制Bezier曲线,并通过实际案例分析,展示动态曲线的实现以及曲线动画与交互效果的开发。
4.1 JavaScript中绘制Bezier曲线的方法
4.1.1 HTML5 Canvas与Bezier曲线
HTML5 Canvas是一个功能强大的2D图形绘制API,它提供了多种绘制方法,包括绘制线条、矩形、圆形以及复杂的图形,如Bezier曲线。Bezier曲线在Canvas中通过 bezierCurveTo 方法实现。该方法需要三个参数:两个控制点坐标和一个终点坐标。
下面是一个简单的例子,展示了如何在Canvas上绘制一个三次Bezier曲线:
<!DOCTYPE html>
<html>
<head>
<title>Bezier Curve Example</title>
</head>
<body>
<canvas id="myCanvas" width="500" height="500"></canvas>
<script>
var canvas = document.getElementById('myCanvas');
if (canvas.getContext) {
var ctx = canvas.getContext('2d');
// 移动到起始点
ctx.moveTo(75, 250);
// 绘制三次Bezier曲线
ctx.bezierCurveTo(75, 25, 375, 25, 375, 250);
// 完成绘制
ctx.stroke();
}
</script>
</body>
</html>
4.1.2 Web API中相关属性和方法
除了 bezierCurveTo 方法,Canvas的Web API还提供了其他一些属性和方法来增强Bezier曲线的绘制能力。例如,可以通过 setLineDash 设置虚线模式, lineWidth 属性来设置线宽等。
下面的代码展示了如何绘制虚线的Bezier曲线:
ctx.setLineDash([5, 15]); // 设置虚线模式,5像素实线后跟15像素空白
ctx.lineWidth = 2; // 设置线宽为2
4.2 实际案例分析
4.2.1 动态绘制曲线的实现
在Web应用中,动态绘制Bezier曲线是一个常见需求,例如实现一个简单的数字签名功能。以下是一个动态绘制曲线的基本示例:
<!DOCTYPE html>
<html>
<head>
<title>Dynamic Bezier Curve Example</title>
</head>
<body>
<canvas id="myCanvas" width="500" height="500"></canvas>
<script>
var canvas = document.getElementById('myCanvas');
if (canvas.getContext) {
var ctx = canvas.getContext('2d');
var isDrawing = false;
var startX = 0;
var startY = 0;
var controlX = 0;
var controlY = 0;
var endX = 0;
var endY = 0;
canvas.addEventListener('mousedown', function(e) {
isDrawing = true;
startX = e.pageX - canvas.offsetLeft;
startY = e.pageY - canvas.offsetTop;
});
canvas.addEventListener('mousemove', function(e) {
if (isDrawing) {
controlX = e.pageX - canvas.offsetLeft;
controlY = e.pageY - canvas.offsetTop;
ctx.clearRect(0, 0, canvas.width, canvas.height);
ctx.beginPath();
ctx.moveTo(startX, startY);
ctx.bezierCurveTo(controlX, controlY, controlX, controlY, startX, startY);
ctx.stroke();
}
});
canvas.addEventListener('mouseup', function(e) {
if (isDrawing) {
endX = e.pageX - canvas.offsetLeft;
endY = e.pageY - canvas.offsetTop;
ctx.clearRect(0, 0, canvas.width, canvas.height);
ctx.beginPath();
ctx.moveTo(startX, startY);
ctx.bezierCurveTo(controlX, controlY, endX, endY, startX, startY);
ctx.stroke();
isDrawing = false;
}
});
}
</script>
</body>
</html>
在此代码中,我们为Canvas添加了 mousedown 、 mousemove 和 mouseup 事件监听器,以捕捉用户的鼠标动作,并实时绘制出相应的Bezier曲线。
4.2.2 曲线动画与交互效果
为了给用户带来更丰富的交互体验,可以通过JavaScript实现Bezier曲线的动画效果。一个常见的方法是使用 requestAnimationFrame 函数,它可以在浏览器重绘之前请求执行一个动画帧。
以下是一个创建Bezier曲线动画的示例:
var animationID = null;
function animateBezier() {
if (animationID) {
cancelAnimationFrame(animationID);
}
animationID = requestAnimationFrame(animate);
}
function animate() {
// 更新控制点坐标以创建动画效果
controlX += 0.5;
controlY += 0.5;
// 清除画布
ctx.clearRect(0, 0, canvas.width, canvas.height);
// 绘制Bezier曲线
ctx.beginPath();
ctx.moveTo(startX, startY);
ctx.bezierCurveTo(controlX, controlY, controlX, controlY, startX, startY);
ctx.stroke();
// 持续动画
animateBezier();
}
animateBezier();
在这个例子中, animateBezier 函数通过 requestAnimationFrame 来请求动画帧,并在每一帧中更新控制点的坐标,从而创建出动画效果。通过这种方式,可以实现平滑的曲线动画,并且与用户的交互行为相结合,从而提升用户体验。
在本章节中,我们详细探讨了如何使用JavaScript和HTML5 Canvas绘制Bezier曲线。我们从基本的绘制方法开始,逐步深入到动态绘制和曲线动画的实现。通过实际案例分析,我们展示了如何将这些技术应用到实际的Web开发中,实现具有交互效果的曲线绘制和动画。在下一章节中,我们将继续探索Bezier曲线在动画与游戏开发中的应用。
5. Bezier曲线在动画与游戏开发中的应用
在现代动画和游戏开发中,Bezier曲线被广泛使用以创建流畅的路径和动画效果。由于其数学特性和易于控制的性质,设计师和开发者可以利用Bezier曲线来精确地控制动画的运动轨迹,同时也为复杂物理模拟提供支持。本章将深入探讨Bezier曲线在动画与游戏开发中的具体应用,包括如何通过设计曲线来实现平滑动画,以及如何将曲线技术用于游戏中的路径追踪和物理模拟。
5.1 动画路径的Bezier曲线设计
为了实现一个流畅和自然的动画,设计师需要精心设计动画的路径。Bezier曲线提供了一个强大的工具,通过它能够定义和调整动画路径,使之既符合动画的节奏,又能保持视觉上的连贯性。
5.1.1 实现平滑动画的关键
平滑的动画不仅能够增强用户体验,还能提高游戏的沉浸感。Bezier曲线之所以适合用于动画路径设计,是因为它能够创建出连续的、无突变的运动轨迹。
-
连续性和可控性 :Bezier曲线具有良好的连续性,可以通过调整控制点来细微改变曲线形状,实现各种复杂的动画路径。每一阶的Bezier曲线都有特定数量的控制点,这些控制点决定了曲线的方向和曲率,从而影响动画路径的流动。
-
灵活的动画控制 :在设计动画时,设计师可以对曲线的各个控制点进行微调,通过增加控制点的数量和调整其位置,来实现更复杂的动画效果。这样的特性使得Bezier曲线成为设计师手中灵活的动画工具。
5.1.2 动画性能优化的策略
动画性能的优化是任何动画和游戏开发中的关键因素。使用Bezier曲线可以有效减少动画过程中的计算量,提升动画运行效率。
-
减少关键帧数量 :通过使用Bezier曲线,设计师可以减少在动画序列中必须手动定义的关键帧数量。曲线的连续性允许系统自动计算中间帧,从而减轻了计算负担。
-
使用缓动函数 :在动画中应用缓动函数,可以让动画从一个关键帧到另一个关键帧的过渡更加自然。Bezier曲线可以作为缓动函数的基础,因为它们本身就具有良好的平滑性和连续性,能够创造出各种缓动效果。
5.2 游戏开发中的应用实例
在游戏开发中,Bezier曲线的使用不仅仅限于动画。实际上,Bezier曲线可用于设计角色的移动路径、实现物理模拟中的平滑曲线轨迹,以及增强游戏视觉效果的动态效果。
5.2.1 路径追踪与角色移动
在很多游戏设计中,角色需要沿着特定路径移动,以完成任务、达到目标或者与游戏环境互动。Bezier曲线在此过程中扮演了关键角色。
-
实现复杂的追踪路径 :游戏中角色或对象的移动路径往往需要符合特定的形状。使用Bezier曲线可以轻松创建出复杂且平滑的路径,进而增强游戏关卡设计的多样性。
-
动态路径生成 :在实时游戏开发中,有时需要根据玩家的操作实时生成路径。Bezier曲线可以作为算法的一部分,动态计算出角色移动的路径,为游戏提供流畅的体验。
5.2.2 贝塞尔曲线在游戏物理中的应用
在游戏物理中,Bezier曲线不仅可以用于视觉效果的展示,还可以用来模拟更复杂的物理行为。
-
平滑曲线轨迹 :在模拟飞行动态或车辆行驶轨迹时,Bezier曲线可以确保轨迹的平滑性,这对于模拟真实的物理环境至关重要。
-
碰撞检测和响应 :在许多游戏中,对角色或物体的移动路径进行精确控制能够有效地执行碰撞检测和响应策略。Bezier曲线可作为这种精确控制的工具,提高物理计算的效率和准确性。
通过本章节的探讨,我们了解了Bezier曲线在动画和游戏开发中的广泛应用和重要价值。在下一章中,我们将深入分析Bezier曲线在实现复杂动画和游戏物理中的具体代码实现。
6. Bezier曲线源代码包解读
6.1 源代码包内容概览
6.1.1 文件结构与模块划分
在对Bezier曲线相关的源代码包进行解读之前,首先要了解整个项目的文件结构和模块划分。典型的源代码包会包含以下几种文件或目录:
-
README.md:项目的说明文件,通常包含安装指南、使用方法和贡献指南。 -
LICENSE:许可证文件,说明了软件的合法使用条件。 -
package.json:项目依赖和配置的清单文件,也用于定义npm包的元数据。 -
src/:源代码目录,包含所有JavaScript或TypeScript源文件。 -
dist/:构建输出目录,存放打包后的代码文件。 -
test/:测试代码目录,存放相关的单元测试和集成测试代码。
源代码模块的划分通常遵循功能模块化原则,例如:
-
bezier.js:核心算法实现。 -
curve.js:曲线操作和计算相关的方法。 -
animation.js:与动画控制相关的接口。 -
game-engine.js:游戏引擎相关的封装。
6.1.2 源代码的组织方式
源代码的组织方式影响着项目的可维护性和可扩展性。通常情况下,源代码组织会采用以下方式:
- 单一职责原则 :每个文件、函数和模块都应当只负责一项任务。
- 模块化 :通过将代码拆分为可复用的模块来降低复杂度。
- ES6模块化语法 :利用
import和export语句来实现模块间依赖关系。 - 文件命名规范 :使用有意义的文件名和目录结构来反映文件内容。
例如,在 src 目录下,我们可能有如下文件:
src/
|-- utils/
| |-- easing.js
| |-- math.js
|-- bezier.js
|-- curve.js
|-- index.js
在这个例子中, easing.js 可能包含动画缓动函数, math.js 提供基础的数学计算工具,而 bezier.js 是核心的贝塞尔曲线计算模块。
6.2 核心函数与算法实现
6.2.1 关键算法函数分析
贝塞尔曲线的核心算法可以通过多个函数来实现,其中最典型的是计算特定点的贝塞尔曲线值。下面是一个计算贝塞尔曲线点的函数示例:
// 计算给定控制点数组的贝塞尔曲线值
function calculateBezierPoint(points, t) {
// points: [x0, y0, x1, y1, ..., xn, yn]
// t: [0, 1]之间的参数
let n = points.length / 2 - 1;
let result = 0;
for (let k = 0; k <= n; k++) {
let term = Math.pow(1 - t, n - k) * Math.pow(t, k);
let xk = points[2 * k];
let yk = points[2 * k + 1];
result += term * (xk + yk);
}
return result;
}
在这段代码中:
-
points是一个包含贝塞尔曲线控制点坐标的数组。 -
t是曲线参数,它在0到1之间变化,决定了曲线上的某个点。 - 函数通过组合控制点坐标和参数
t计算出曲线上的点。
6.2.2 注释与代码维护的最佳实践
代码注释是维护代码可读性的重要方面。好的注释可以解释代码的意图和实现逻辑,帮助开发者理解代码的工作原理。
/**
* 根据给定的控制点数组和参数t计算贝塞尔曲线上的点
* @param {Array} points - 一个二维数组,包含了所有控制点的坐标,形如[[x0, y0], [x1, y1], ..., [xn, yn]]
* @param {number} t - 曲线参数,范围[0, 1]
* @returns {number} - 返回计算得到的曲线上的点的坐标值
*/
这段注释使用了JSDoc格式,它是一种常用的JavaScript文档注释风格,可以让开发者通过特定工具生成文档。
在进行代码维护时,应该定期回顾并更新代码注释,以确保它们与代码实现保持同步。当代码发生变化时,相关的注释也应该相应地进行调整。
6.2.3 实际应用中的算法优化
在实际应用中,算法优化是提高性能和响应速度的关键。针对贝塞尔曲线的计算,可以采取以下优化策略:
- 缓存计算结果 :对于重复使用的计算结果,可以先计算并缓存起来,以避免重复计算。
- 减少不必要的计算 :避免在循环中进行不必要的计算,特别是在内循环中。
- 使用高效的数学算法 :例如,使用快速幂算法代替简单的重复乘法,可以显著提高性能。
例如,针对计算贝塞尔曲线点的函数,可以进行如下优化:
// 计算给定控制点数组的贝塞尔曲线值,并缓存结果
function calculateBezierPointOptimized(points, t) {
// ...(省略具体的优化实现代码)
}
在这个优化版本中,可以考虑使用一个映射或数组来存储中间计算结果,或者根据 t 值的不同将结果分段计算以重用结果。
6.2.4 代码实现的可扩展性
在开发涉及复杂算法的项目时,可扩展性是一个重要的考虑因素。可扩展的代码允许未来在不需要完全重写现有逻辑的情况下添加新功能。
例如,对于贝塞尔曲线库来说,未来可能需要支持更多种类的曲线(如双二次或三次曲线)。为了实现这一点,可以在编写代码时预留扩展接口:
class BezierCurve {
constructor(points) {
this.points = points;
}
// 添加一个方法来计算曲线上的点
calculatePoint(t) {
// ...(使用算法计算点)
}
// 扩展方法以支持新的曲线类型
addCurveType(type, implementation) {
this[type] = implementation;
}
}
在这个例子中, addCurveType 方法允许在 BezierCurve 类上动态添加新的曲线类型和相应的实现方法。
6.2.5 单元测试与代码质量保证
在开发涉及复杂算法的代码时,单元测试是保证代码质量的重要手段。单元测试可以确保各个模块按预期工作,并在代码更新时及时发现回归错误。
例如,对于贝塞尔曲线的计算函数,单元测试可能包括:
- 验证曲线是否通过所有控制点。
- 测试不同
t值时曲线点的计算结果。 - 测试曲线是否平滑(例如,连续性和导数的一致性)。
function testBezierCurve() {
let curve = new BezierCurve([0,0, 1,1, 2,0]);
assert.equal(curve.calculatePoint(0), 0, '起点测试');
assert.equal(curve.calculatePoint(0.5), 1, '中点测试');
assert.equal(curve.calculatePoint(1), 2, '终点测试');
// ...更多的测试用例
}
在这里, assert 对象是断言库的一部分,用于验证代码运行结果是否符合预期。
6.2.6 性能基准测试与优化
性能基准测试可以帮助开发者了解算法的运行效率,并对比不同算法实现之间的性能差异。这对于优化性能至关重要,尤其是当涉及到图形界面动画或游戏开发时。
在JavaScript中,可以使用基准测试工具如Benchmark.js来测量代码片段的性能:
const Benchmark = require('benchmark');
const suite = new Benchmark.Suite;
// 添加测试项
suite.add('Bezier', function() {
// 在这里执行贝塞尔曲线计算
})
// ...添加更多的测试项
// 运行测试
suite
.on('cycle', function(event) {
console.log(String(event.target));
})
.on('complete', function() {
console.log('Fastest is ' + this.filter('fastest').map('name'));
})
.run({'async': true});
在这个基准测试示例中,测试套件 suite 会运行每个测试项多次,并输出每次迭代的性能数据。最后,它会告诉你哪个测试项运行得最快。
通过基准测试,开发者可以发现性能瓶颈,并针对性地进行优化,以提升代码的整体性能。
7. Bezier曲线优化技术探讨
7.1 Bezier曲线性能优化方法
在计算机图形学中,Bezier曲线的计算效率是图形渲染和动画设计中一个不可忽视的问题。尤其是在复杂的动画或游戏场景中,成千上万的曲线如果处理不当,会大大降低渲染效率。这里我们探讨几种常用的性能优化方法。
7.1.1 利用缓存和离屏渲染
缓存是提高性能的一种常见方式,我们可以预先计算并存储常见的或静态的Bezier曲线。另外,对于动态变化的曲线,可以通过离屏渲染(off-screen rendering)来减少重绘次数,例如,在动画的每一帧中只对变化的部分进行更新。
7.1.2 简化曲线表示
在一些场合下,可以将高阶的Bezier曲线简化为低阶曲线而不损失太多的视觉效果,这有助于减少计算量。例如,四阶曲线可以分解为两个三阶曲线,而三阶曲线又可以分解为两个二次曲线,以此类推。
7.1.3 硬件加速
现代图形处理单元(GPU)具备处理复杂图形计算的能力。通过利用GPU加速,可以将部分或全部Bezier曲线的计算任务交给GPU去处理,从而将CPU的负担转移到GPU上。
7.2 Bezier曲线的递归优化策略
De Casteljau算法虽然直观且数学表达简单,但是在递归计算中可能会有性能问题。因此,我们可以通过一些技术手段来减少递归的深度,或转而使用迭代方法来计算Bezier曲线。
7.2.1 分段线性逼近
我们可以将Bezier曲线分成多个小段,然后用线段来近似逼近,每个小段使用线性插值来计算。这种方法在视觉上不会造成太大差异,但在计算上大大减少了复杂度。
7.2.2 动态调整递归深度
通过观察曲线的曲率或计算误差,动态地调整递归的深度。在曲率小,误差允许的情况下减少递归深度,在需要细节的地方增加递归深度。
7.2.3 基于迭代的算法
迭代算法可以减少递归带来的栈空间消耗,同时也有助于优化性能。通过循环结构代替递归,可以更好地控制计算流程,并且易于实现并行化处理。
7.3 Bezier曲线在WebGL中的应用
WebGL是一个基于OpenGL ES的JavaScript API,能够直接在网页中渲染复杂的2D和3D图形。Bezier曲线在WebGL中的应用可以结合GPU的强大计算能力,实现高效渲染。
7.3.1 WebGPU与Bezier曲线
WebGPU是WebGL的后继者,它提供了更接近原生性能的Web API,让开发者在浏览器中获得更优的图形处理能力。Bezier曲线的渲染和动画可以利用WebGPU的高速缓存和异步计算特性。
7.3.2 实例:GPU驱动的曲线动画
在WebGL或WebGPU中实现GPU驱动的曲线动画,需要定义相应的着色器(shader)来处理曲线数据。利用GPU并行处理的能力,可以同时计算成百上千个控制点的曲线。
// GLSL Vertex Shader 示例代码
#version 300 es
in vec2 a_position; // 控制点位置
uniform float t; // 参数变量
void main() {
// 计算当前参数t对应的Bezier曲线上的点
float u = 1.0 - t;
float tt = t * t;
float uu = u * u;
float uuu = uu * u;
float ttt = tt * t;
vec2 point = uuu * a_position[0] +
3.0 * uu * t * a_position[1] +
3.0 * u * tt * a_position[2] +
ttt * a_position[3];
gl_Position = vec4(point, 0.0, 1.0);
}
以上是一个简化的顶点着色器代码,用于计算给定参数 t 的Bezier曲线上的点。
7.4 Bezier曲线的软件工具支持
在设计软件中,如Adobe Illustrator、AutoCAD等,Bezier曲线有着广泛的应用。这些软件通常会提供一些辅助工具来帮助设计人员更高效地使用Bezier曲线。
7.4.1 曲线编辑器功能
在复杂的图形设计软件中,通常会有曲线编辑器来帮助用户进行控制点的选择、移动以及曲线的实时预览。这些工具大大降低了Bezier曲线操作的复杂性。
7.4.2 插件与扩展
许多设计软件支持插件或扩展功能,第三方开发者可以根据这些平台的API开发出能够提供高级Bezier曲线编辑能力的工具。
7.5 Bezier曲线的未来发展趋势
随着技术的进步,Bezier曲线的应用领域正在不断拓展。未来,它可能会与人工智能、机器学习等领域相结合,开拓出新的应用空间。
7.5.1 智能化曲线设计
利用机器学习模型,可以从大量的设计样本中学习曲线的规律,智能生成美观的Bezier曲线。这在工业设计、建筑设计等领域具有巨大的潜力。
7.5.2 跨学科应用探索
在数据可视化、虚拟现实等新领域中,Bezier曲线也可能扮演重要角色,例如,通过智能算法优化数据点之间的过渡,以实现更自然的视觉效果。
简介:贝塞尔曲线是一种在计算机图形学中被广泛使用的参数曲线,由法国工程师皮埃尔·贝塞尔提出。它在设计、动画、游戏开发和路径规划等多领域有着重要应用。通过控制点定义形状,贝塞尔曲线可通过阶数不同的多项式表示,并通过De Casteljau算法简化计算。在JavaScript环境中,使用贝塞尔曲线可以创建动态效果,并且贝塞尔曲线的源代码包可能包含必要的实现文件。掌握贝塞尔曲线对于数字艺术和软件开发都具有重要价值。
























 1473
1473

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








