文章目录
一、前言背景
笔者最近在学习运算放大器的基本知识,写下此博客用作记录和分享学习笔记。如有不对还望各网友大神指正,本博客大量借鉴资料,笔者只是拾人牙慧的小屁孩。
笔者在阅读《Op Amps for Everyone》时,对反相比例运算电路中
R
G
R_{G}
RG不能大于
R
F
R_{F}
RF的问题颇具疑惑,在查询资料和反复思考中,得到了一定见解。

二、反馈与稳定性理论
(一)、传递函数中的极点和零点
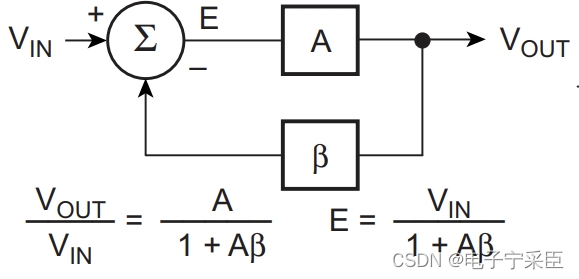
这是一个标准的反馈环路框图,当我们对其分析时,我们可以利用求解方程的方式对其进行化简:
在框图求和的结果处设定一个辅助函数
E
E
E,
E
=
V
I
N
−
β
V
O
U
T
E = V_{IN} - \beta V_{OUT}
E=VIN−βVOUT
又因为
V
O
U
T
=
E
A
V_{OUT} = EA
VOUT=EA,合并消除
E
E
E可得
V
O
U
T
V
I
N
=
A
1
+
A
β
\frac{V_{OUT}}{V_{IN}} = \frac{A}{1+ A\beta}
VINVOUT=1+AβA
故,
E
=
V
I
N
−
β
V
O
U
T
=
V
I
N
1
+
A
β
E = V_{IN} - \beta V_{OUT} = \frac{V_{IN}}{1 + A\beta}
E=VIN−βVOUT=1+AβVIN。
在这里,我们把
V
O
U
T
V
I
N
=
A
1
+
A
β
\frac{V_{OUT}}{V_{IN}} = \frac{A}{1+ A\beta}
VINVOUT=1+AβA称为闭环增益,
A
β
A\beta
Aβ称为环路增益,
E
=
V
I
N
1
+
A
β
E = \frac{V_{IN}}{1 + A\beta}
E=1+AβVIN称为误差。
请记住,计算中使用的都是复数,复数具有幅值和方向。
我们可以根据此类传递函数绘制其对应的伯德图。(对不熟悉信号处理的读者来说,传递函数就是以 s = w j s = wj s=wj为自变量、在复数域的转移特性;而伯德图使用形如 20 lg ( F ( t ) ) = 20 lg ( ∣ F ( t ) ∣ ) + j θ 20\lg{(F(t))} = 20\lg{(|F(t)|)} + j \theta 20lg(F(t))=20lg(∣F(t)∣)+jθ,其中 θ \theta θ为辐角,的对数公式进行图像描述)
而在伯德图上,极易令人关注的点为极点和零点。
举个例子:对于一个带阻滤波器,可得到如下传递函数


我们将传递函数上分母为零的转折点,称为极点,在幅频特性上反映为向下倾斜的直线;接着将传递函数上分子为零的转折点,称为零点,在幅频特性上反映为向上倾斜的直线。
零点:当系统输入幅度不为零且输入频率使系统输出为零时,此输入频率值即为零点。
极点:当系统输入幅度不为零且输入频率使系统输出为无穷大(系统稳定破坏,发生振荡)时,此频率值即为极点。
将其分段进行绘制

并利用
s
→
0
s \rightarrow 0
s→0,
G
→
1
2
G \rightarrow \frac{1}{2}
G→21;
s
→
∞
s \rightarrow \infty
s→∞,
G
→
1
G \rightarrow 1
G→1确定两端,之后将曲线整合到一张图中可得到粗略的伯德图:

每一个极点之处,增益衰减-3dB,并移相-45度。极点之后每十倍频,增益下降20dB。
零点与极点相反;每一个零点之处,增益增加3dB,并移相45度。零点之后,每十倍频,增益增加20dB。
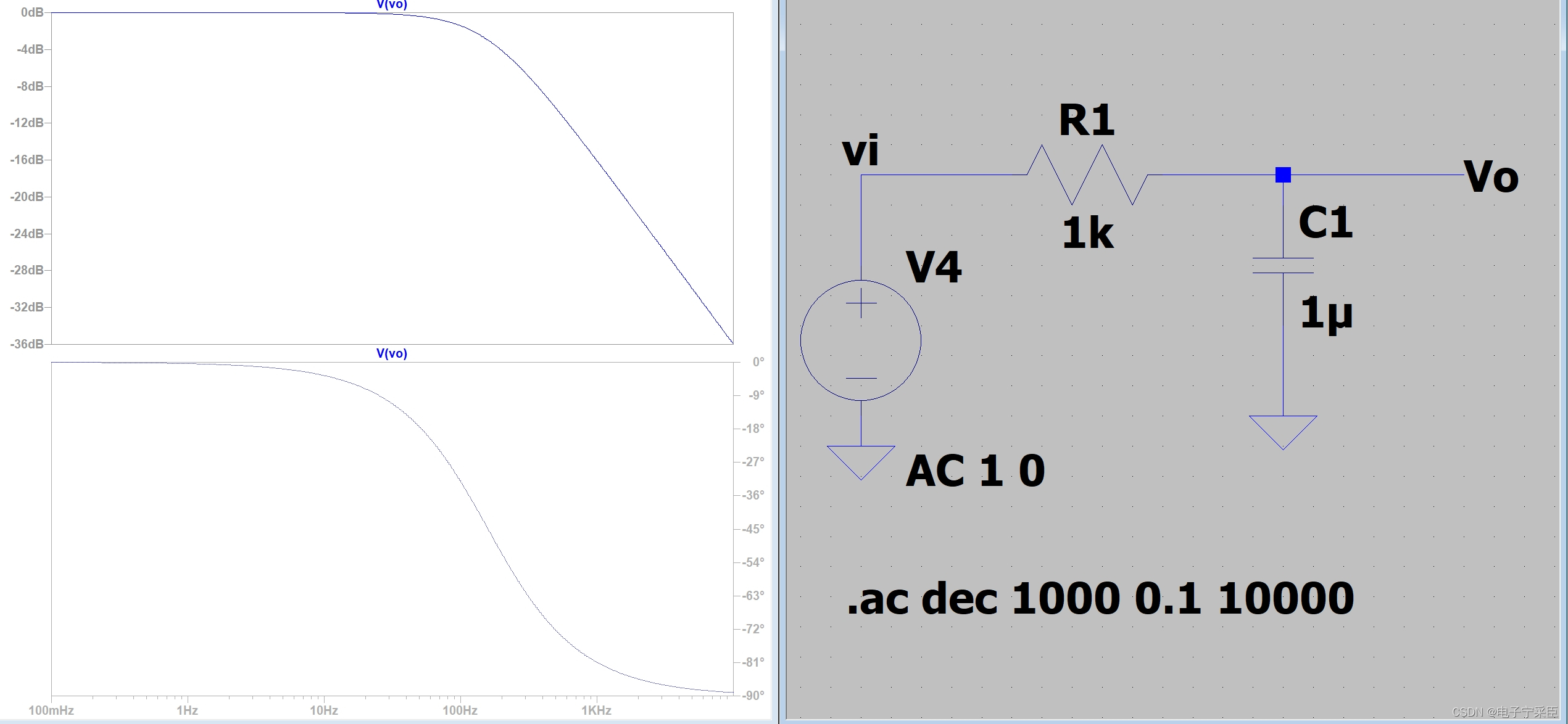
可以看见当在极点频率处,增益衰减-3dB,并移相-45度。
当然,当传递函数中存在N多极点或零点时,其相位和增益都是相互叠加作用的结果。
知道了这些对我们理解运放有什么用呢?
举个极端的例子方便你的理解——当环路增益(
A
β
A\beta
Aβ)趋近于
−
1
-1
−1时(
1
∠
−
180
°
1\angle{-180°}
1∠−180°),其闭环增益(
V
O
U
T
V
I
N
=
A
1
+
A
β
\frac{V_{OUT}}{V_{IN}} = \frac{A}{1+ A\beta}
VINVOUT=1+AβA)趋近于
1
/
0
=
∞
1/0=\infty
1/0=∞。理论上,如果没有能量限制或者别的什么非线性限制,运放将放大当前信号到无穷大。这就说明你的输出在不受控制的振荡了。
(二)、把运放代入伯德图
现在我们将目光放在运放上,首先考虑理想运放,当其工作在负反馈时,其模型与上诉模型一致,故我们也可以得出运放的闭环增益为:
V
O
U
T
V
I
N
=
A
1
+
A
β
\frac{V_{OUT}}{V_{IN}} = \frac{A}{1+ A\beta}
VINVOUT=1+AβA。
我们对两边取对数,并绘制其伯德图:
20
lg
(
V
O
U
T
V
I
N
)
=
20
lg
(
A
)
−
20
lg
(
1
+
A
β
)
20\lg{(\frac{V_{OUT}}{V_{IN}})} =20\lg{(A)}-20\lg{(1+ A\beta)}
20lg(VINVOUT)=20lg(A)−20lg(1+Aβ)

在这张伯德图中不存在任何能提供负相移的极点,电路不会振荡。
但是这种运放的理想特性是目前所没有的。真实运放会因为内部的多个电容而喜获多个极点。
这会让运放随着频率升高,内部的寄生电容对应的极点效应累积起来,环路增益(
A
β
A\beta
Aβ)迅速到达
1
∠
−
180
°
1\angle{-180°}
1∠−180°,导致不稳定。
于是集成电路设计师选择“如果打不过对方,就加入对方”的策略,通过在运放内部增加补偿电容的方法,有意地为运放引入了一个主要的极点。
单极点运放:
A
=
a
1
+
j
w
w
a
A = \frac{a}{1 + j \frac{w}{w_{a}}}
A=1+jwawa

我们常说的单位增益频率也就是0dB和电路开环增益(
A
A
A)的交点频率,当开环增益小于1时,内部寄生电容效应迅速累积,使环路增益(
A
β
A\beta
Aβ)快速达到
1
∠
−
180
°
1\angle{-180°}
1∠−180°。
(三)、环路增益图助力理解稳定性
稳定性由环路增益(
A
β
A\beta
Aβ)决定。
当环路增益(
A
β
A\beta
Aβ)等于
−
1
=
∣
1
∣
∠
−
180
°
-1 = |1|\angle{-180°}
−1=∣1∣∠−180°时,系统将会变得不稳定甚至振荡。
当我们在设计放大器的频率特性时,必须注意不要让环路增益的相移累积到
−
180
°
-180°
−180°。
在相移接近
−
180
°
-180°
−180°,就会出现诸如振铃或过冲等问题。
需要理解的是,传递函数的相位特性是系统对不同频率的输入信号产生的相位变化,即延时特性。当相移越接近
−
180
°
-180°
−180°,我们也称相位裕度越小时,此时,输出信号相对于输入信号滞后了接近
180
°
180°
180°,此时它们的误差是相对较大的,系统需要更多的时间进行调节,此时会存在更长的稳定时间和较大的瞬态误差。
这里我模拟了
A
β
A\beta
Aβ的模值为
1
1
1时,但滞后相位是变量的例子,帮助大家理解:
当相位裕度为
170
°
170°
170°时,

当相位裕度为
10
°
10°
10°时,

可以看出,当相位裕度越大,过冲(超调)越小,系统越稳定(但稳定的时间更长),但同时响应速度也会减慢(因为Error的幅值更小)。
三、反相比例运算电路的分析
(一)、对反相比例运算电路做衰减时进行稳定性分析
在平时使用运算放大器时,我们通常使用理想运算放大器进行分析,在计算需要的闭环增益时,我们通常假设运放的开环增益
a
→
∞
a \rightarrow \infty
a→∞(由于是理想运算放大器,故电路的开环增益为
A
→
∞
A \rightarrow \infty
A→∞),故此时的闭环增益为:
lim
A
→
∞
A
1
+
A
β
=
1
β
\lim\limits_{A \rightarrow \infty}{\frac{A}{1+ A\beta}}=\frac{1}{\beta}
A→∞lim1+AβA=β1。
就比如反相比例运算电路,
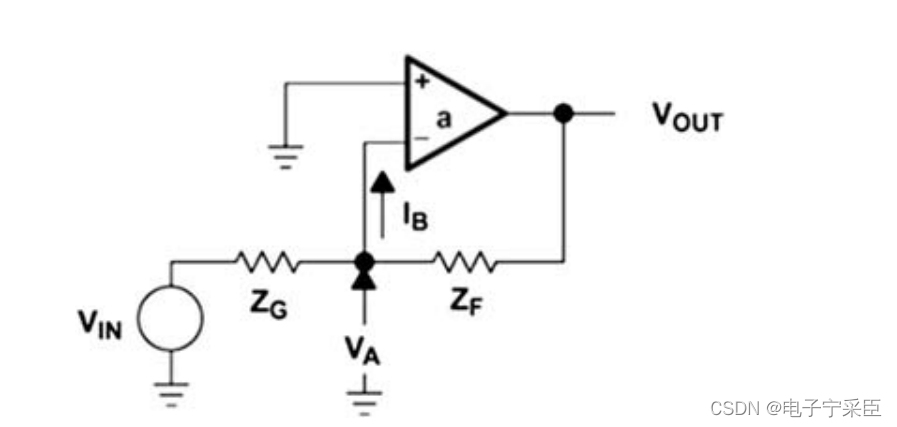
我们对
V
A
V_{A}
VA列出结点方程:
V
A
=
V
I
N
(
Z
F
/
(
Z
F
+
Z
G
)
)
+
V
O
U
T
(
Z
G
/
(
Z
F
+
Z
G
)
)
V_{A} = V_{IN}(Z_{F}/(Z_{F}+Z_{G}))+V_{OUT}(Z_{G}/(Z_{F}+Z_{G}))
VA=VIN(ZF/(ZF+ZG))+VOUT(ZG/(ZF+ZG))
我们再假设运放为高阻(
I
B
=
0
I_{B} = 0
IB=0),
再接合
V
O
U
T
=
−
a
V
A
V_{OUT} = -aV_{A}
VOUT=−aVA,
则给推出
V
O
U
T
V
I
N
=
−
a
Z
F
Z
F
+
Z
G
1
+
a
Z
G
Z
F
+
Z
G
\frac{V_{OUT}}{V_{IN}}=\frac{\frac{-aZ_{F}}{Z_{F}+Z_{G}}}{1+ \frac{aZ_{G}}{Z_{F}+Z_{G}}}
VINVOUT=1+ZF+ZGaZGZF+ZG−aZF。
以此作为反相比例运算电路的闭环增益。
需要注意的是,此时的电路的开环增益为
A
=
−
a
Z
F
Z
F
+
Z
G
A=\frac{-aZ_{F}}{Z_{F}+Z_{G}}
A=ZF+ZG−aZF,反馈因子为
β
=
−
Z
G
Z
F
\beta=-\frac{Z_{G}}{Z_{F}}
β=−ZFZG。
在这里,值得区分的是电路的开环增益(
A
=
−
a
Z
F
Z
F
+
Z
G
A=\frac{-aZ_{F}}{Z_{F}+Z_{G}}
A=ZF+ZG−aZF)和运放的开环增益(
a
a
a)有所不同。利用这个电路的开环增益和反馈因子,我们可以得到这个电路的环路增益:
A
β
=
−
a
Z
F
Z
F
+
Z
G
⋅
−
Z
G
Z
F
=
a
Z
G
Z
F
+
Z
G
A\beta = \frac{-aZ_{F}}{Z_{F}+Z_{G}} \cdot -\frac{Z_{G}}{Z_{F}} = \frac{aZ_{G}}{Z_{F}+Z_{G}}
Aβ=ZF+ZG−aZF⋅−ZFZG=ZF+ZGaZG
如果,这是一个牛比的理想运算放大器,则有
lim
a
→
∞
(
V
O
U
T
V
I
N
)
=
lim
a
→
∞
(
−
a
Z
F
Z
F
+
Z
G
1
+
a
Z
G
Z
F
+
Z
G
)
=
−
Z
F
Z
F
+
Z
G
⋅
Z
F
+
Z
G
Z
G
=
−
Z
F
Z
G
\lim\limits_{a \rightarrow \infty}(\frac{V_{OUT}}{V_{IN}}) =\lim\limits_{a \rightarrow \infty} ( \frac{\frac{-aZ_{F}}{Z_{F}+Z_{G}}}{1+ \frac{aZ_{G}}{Z_{F}+Z_{G}}} )= \frac{-Z_{F}}{Z_{F}+Z_{G}} \cdot \frac{Z_{F}+Z_{G}}{Z_{G}} = \frac{-Z_{F}}{Z_{G}}
a→∞lim(VINVOUT)=a→∞lim(1+ZF+ZGaZGZF+ZG−aZF)=ZF+ZG−ZF⋅ZGZF+ZG=ZG−ZF,就是等于
1
β
\frac{1}{\beta}
β1。
但是,您也知道,目前我们并未生成出理想运算放大器,所以这个运放的开环增益(
a
a
a)是无法实现恒定的无穷的,并且其对应的电路的环路增益也会对应的引入极点。
电路的环路增益(
A
β
=
a
Z
G
Z
F
+
Z
G
A\beta = \frac{aZ_{G}}{Z_{F}+Z_{G}}
Aβ=ZF+ZGaZG)如果本身具有不多的相位裕度,而当
Z
F
<
Z
G
Z_{F} < Z_{G}
ZF<ZG时,可以不难发现,环路增益(
A
β
=
a
Z
G
Z
F
+
Z
G
A\beta = \frac{aZ_{G}}{Z_{F}+Z_{G}}
Aβ=ZF+ZGaZG)被增大了,随之相位裕度也减小了。随着相位裕度的减小,过冲(超调)增大,有甚者可能出现振铃,系统越不稳定(但需要稳定的时间更短),但同时响应速度也会变快。

总而言之,由于
Z
F
<
Z
G
Z_{F} < Z_{G}
ZF<ZG,让环路增益增大了,让相位裕度减小了,降低了稳定性。
(二)、搭建仿真验证结果
我们根据其环路增益的原理,断开反馈端,以测试信号测量其环路增益,再从反馈端获取激励信号,从而进行分析。

搭建仿真进行测试:
- 参考1
反馈因子 β = − 1 / 5 \beta=-1/5 β=−1/5
相位裕度测量大约为66°

其时域波形,
- 参考2
反馈因子 β = − 1000 \beta=-1000 β=−1000
相位裕度测量为51.429°

其时域波形,
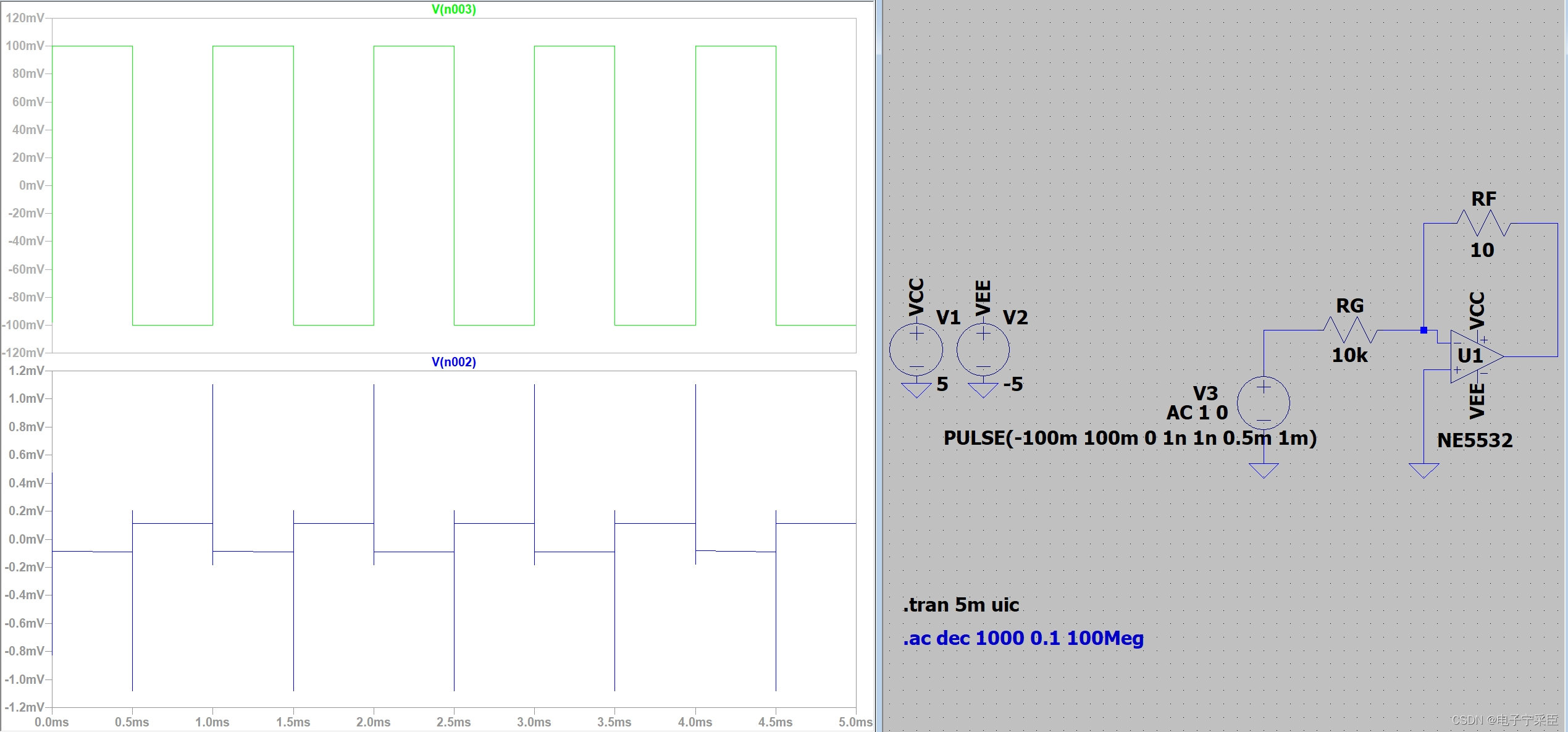
可以看出,在仿真中,对于相位裕度小的系统,其过冲也会相应变大,其系统的稳定性降低。
总结
对于系统的设计需要考虑相位裕度考虑,对应为设计的环路增益的考虑,这与系统的稳定性息息相关。这篇博客仅为一个理论推导和理想仿真,甚至没有考虑容性负载对运放相位裕度的恶化(或者寄生参数,当然也不是所有的寄生参数都会让运放不稳定,有的运放相位裕度补偿甚至会运用寄生电容引入零点等骚套路,以后有机会可以开个新坑)。
总而言之,运放使用时,请牢记,除了运放理想闭环增益是你设计的根本外,还有其动力学特性需要考虑。
参考资料
[1] Bruce Carter, Ron Mancini. Op Amps for Everyone[M]. Fifth Edition. United States: Elsevier Inc, 2018.
[2] 零点和极点的区别及其物理意义























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








