参考文献:
1. RFC1321 - R. Rivest
2. 中山大学 蔡国扬 老师的 Web安全课件
算法概述
- MD5 使用 little-endian,输入任意不定长度信息,以 512 位长进行分组,生成四个32位数据,最后联合起来输出固定 128 位长的信息摘要。
- MD5 算法的基本过程为:求余、取余、调整长度、与链接变量进行循环运算、得出结果。
在 RFC1321 中,算法共分为五步,对于每一步的细节我都会举出例子来更方便的理解。另外有一点需要注意的是,下文中若无特别说明,都是以比特为单位来阐述算法。
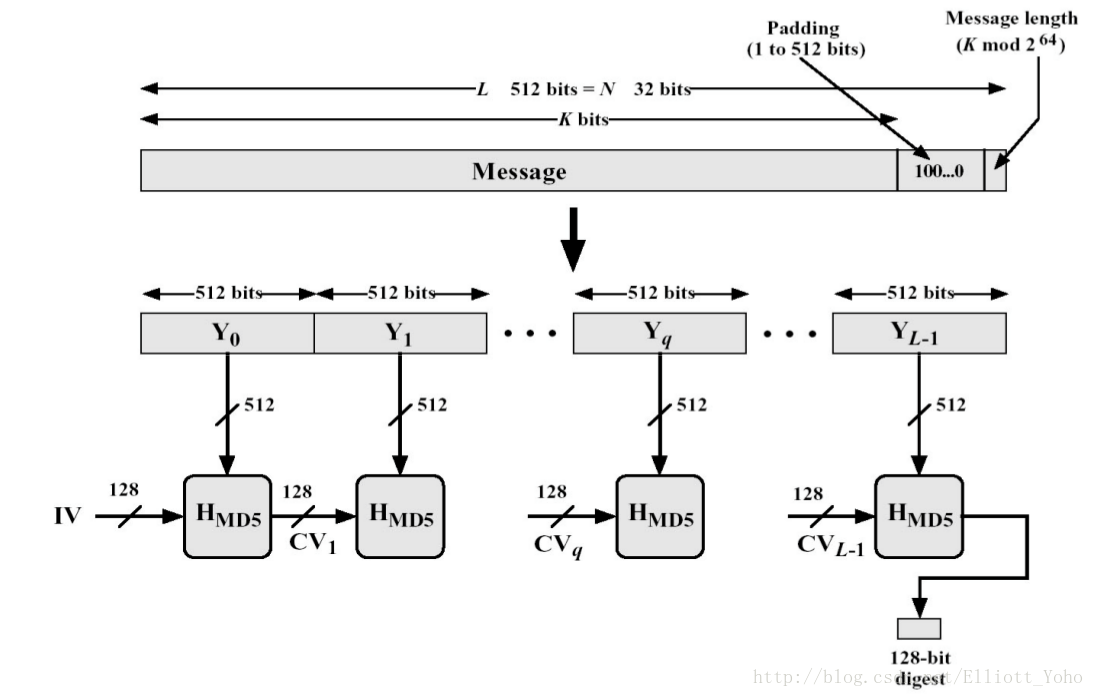
基本流程图
一、Append Padding Bits
在原始消息的尾部进行填充,使得填充后的消息位数 L mod 512 = 448。
填充规则为,先填充一个 1,然后剩余的填充 0。并且填充是必须的,即使原始消息的长度模 512 后正好为 448 比特,也要进行填充。总之,填充的长度至少为 1 比特,最多为 512 比特。
例如,原始消息为 12345678,总长度为 8 * 8 = 64 比特,那么需要填充 384 比特,即填充 1000…. 后面还有 380 个 0。
填充后的消息用 16 进制表示(此处省略 0x)为
31 32 33 34 35 36 37 38 80 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
二、Append Length
计算原始消息(未填充 padding 前)的长度,用长 64 位的 b 表示。若 b 大于 264 ,即 64 位不够表示原始消息的长度时,只取低 64 位。将 b 填充至第一步填充后的消息尾部。
此时,填充后得到的消息总长度为 512 的倍数,也是 16 的倍数。将填充后的消息分割为 L 个 512 位的分组, Y0,Y1,...,YL−1 。
注意,实际填充时不是直接将长度的 64 位二进制表示接上去就可以。而是先用两个 32 位的字来表示原始消息长度 b,将低位的字先填充,然后再填充高位的字,并且每个字在填充时使用 little-endian。
little-endian:将低位字节排放在内存的低地址端,高位字节排放在内存的高地址端。
例如,原始消息为 12345678,总长度为 8 * 8 = 64 比特,用 64 位二进制表示为 00000000 00000000 00000000 00000000 00000000 00000000 00000000 01000000。分成两个 32 位的字:
- 高位:
00000000 00000000 00000000 00000000 - 低位:
00000000 00000000 00000000 01000000
低位字节的 little-endian 表示为 01000000 00000000 00000000 00000000。
因此,应该填充的 64 位为 01000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000。
三、Initialize MD Buffer
初始化一个 128 位的 MD 缓冲区,也表示为 4 个 32 位寄存器 (A, B, C, D),用来迭代计算保存信息摘要。
对于 4 个 32 位的寄存器 A、B、C、D 分别初始化为 16 进制初始值,采用小端规则
| word | little-endian | ||||
|---|---|---|---|---|---|
| A | 01 | 23 | 45 | 67 | 0x67452301 |
| B | 89 | AB | CD | EF | 0xEFCDAB89 |
| C | FE | DC | BA | 98 | 0x98BADCFE |
| D | 76 | 54 | 32 | 10 | 0x10325476 |
四、Process Message in 16-Word Blocks
首先,定义四个轮函数,每个函数以 3 个 32 位字为输入,输出 1 个 32 位字。
| Function | return |
|---|---|
| F(X,Y,Z) | (X∧Y)∨(¬X∧Z) |
| G(X,Y,Z) | (X∧Z)∨(Y∧¬Z) |
| H(X,Y,Z) | X⊕Y⊕Z |
| I(X,Y,Z) | Y⊕(X∨¬Z) |
以第二步分割后的 512 比特的分组为单位,每一个分组 Yq (q = 0, 1, …, L - 1) 经过 4 轮循环的压缩算法,记为 Hmd5 ,对第三步初始化的 MD 缓冲区进行迭代更新,初始 MD 缓冲区记为 CV0=IV ;第 q 个分组处理后的 MD 缓冲区记为 CVq=








 本文详细介绍了MD5加密算法的原理,包括算法概述、填充规则、长度表示、MD缓冲区初始化、消息块处理和输出信息摘要的过程。同时,提供了两种C++实现方法,一种适用于已知长度的原始消息,另一种能处理未知长度的消息。
本文详细介绍了MD5加密算法的原理,包括算法概述、填充规则、长度表示、MD缓冲区初始化、消息块处理和输出信息摘要的过程。同时,提供了两种C++实现方法,一种适用于已知长度的原始消息,另一种能处理未知长度的消息。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 3126
3126

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








