SVM研究（2）

        上回介绍了软间隔的SVM，但是还都是局限于原问题（primal problem）的形式，有一些算法是针对对偶问题（dual problem）提出的，所以这次就把对偶问题推导出来。

        我们对问题做一个简化，将替换为，对应的，每一个样本替换为增加一个维度，这样子就变为。事实表明，这的确是某些算法得以成立的重要步骤。

（1）     L1-SVM的对偶问题

这一部分求解L1-SVM的对偶问题，我们使用带约束的形式，如下：

                        (1)

引入Lagrange乘子和，引入Lagrange函数：

        （2）

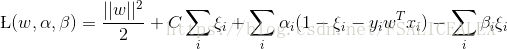
之后，可以需要求解对偶函数：

        （3）

这里指的就是这个向量，同理。

对求导，等于零，得到使得(2)达到最小的：

                                                                    （4）

观察到（2）对于是线性函数，所以极小值是，这样子的对偶函数值没有意义，所以只有当（2）对的导数等于0的时候才有意义，也即满足：

                                                                  （5）

将（4）带入（2），我们可以得到（3）的显示解。当然，因为要满足约束（5）才有意义，我们把约束（5）也要带进去。

带入后为：

                         （6）

即矩阵Q中的元素，设，那么还可以化简为：

                                                  （7）

现在我们可以写出对偶问题：    

                                    （8）

注意，这里是取maximum。我们还可以化简，消去，再将max写成标准的min，得到

                                        （8）'

这就是一个简单的矩形约束的凸二次规划问题啦~

（2）  L2-SVM的对偶问题

上次只是简单的写出了L2-SVM的无约束问题，现在将它化为带约束的形式。无约束的形式是：

（9）

引入松弛变量，令，则变为

                （10）

进一步化为：

                                （11）

接下来的步骤就和L1-SVM中的步骤相同啦，只是对于来说，不是线性函数了，而是二次函数，那么就可以直接求出来使得Lagrange函数最小的，然后带入就行了。这里就不详细讲了。

最后可以得到：

                                            （12）

这里的矩阵与L1-SVM中的有所不同，记L1-SVM中的为，那么（12）中的，是单位阵。相当于在L1-SVM的基础上对进行了一个修正，然后去除了一边的约束。

（3）  原问题和对偶问题的关系

        由优化上的一些理论我们知道，如果问题是凸的，而且满足存在原问题的可行解，那么原问题和对偶问题之间的对偶间隙为0，也就是说两个问题的最优解对应的目标函数值是相同的（这里，对偶问题的目标函数指的就是(3)），这一点其实挺神奇的，因为这毕竟是两个看起来不那么相似的问题。

        我们要处理的问题是一个很简单的二次函数，而且它是凸的，可行解条件也很容易满足。我们还知道对于SVM问题，KKT条件是充要条件，所以，我们可以利用KKT条件去寻找问题的最优解。假设我们求解对偶问题，使用某个算法求得了最优解，之后，我们可以利用其中一个KKT条件得到原问题的最优解 , KKT条件在这里成为了联系原问题和对偶问题的桥梁。

        那么，即使我们求得的不是最优解，我们也可以使用KKT条件获得一个，在逐渐迭代的过程中，逐渐接近对偶问题的最优解，也在接近对偶问题的最优解。不过这个联系并不是很紧密，当的改变使得对偶问题的目标函数上升时（由于是取maximum），由KKT条件得到的却可能使得原始函数的目标函数上升而不是下降，这是由实验得到的结果（具体例子还没有找到，希望看得人能够提供，感谢！）。

      之后，我们再谈谈支持向量的判别。先考虑L1-SVM。由KKT条件中的互补松弛条件，我们知道

                （13）

                                               （14）

这里的、、和都是最优解，就不加标明了。我们可以通过这些条件来从对偶问题的推断出是否是支持向量。不要忘了，对于和还有一个约束

                                （15）

这也是一个KKT条件。

        假如，那么由（15），有，进而由(14)知道，而由（13）知道，所以对应的可能是支持向量，或者也可能是正确分类的样本。

        假如，那么由（15），有，进而，而且由（13）知道，，也即，所以是支持向量。

   假如，那么，，可能是支持向量，也可能是处在这个超平面的里头（见几何意义），就是说被松弛了，也有可能是被误分类了。一般来说，要判断是否是支持向量，只要判断是否大于0就行，不用那么严格。