[bzoj2732][HNOI2012]射箭

2732：[HNOI2012]射箭

Description

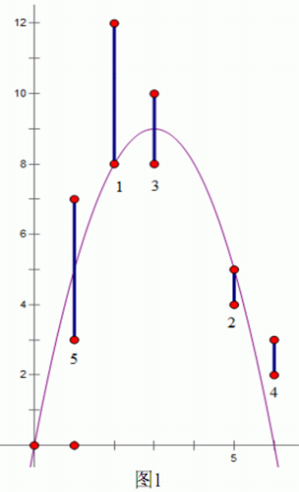
沫沫最近在玩一个二维的射箭游戏，如下图 1 所示，这个游戏中的 x 轴在地面，第一象限中有一些竖直线段作为靶子，任意两个靶子都没有公共部分，也不会接触坐标轴。沫沫控制一个位于(0,0)的弓箭手，可以朝 0 至 90?中的任意角度（不包括 0度和 90度），以任意大小的力量射出带有穿透能力的光之箭。由于游戏中没有空气阻力，并且光之箭没有箭身，箭的轨迹会是一条标准的抛物线，被轨迹穿过的所有靶子都认为被沫沫射中了，包括那些 只有端点被射中的靶子。这个游戏有多种模式，其中沫沫最喜欢的是闯关模式。在闯关模式中，第一关只有一个靶 子，射中这个靶子即可进入第二关，这时在第一关的基础上会出现另外一个靶子，若能够一箭 双雕射中这两个靶子便可进入第三关，这时会出现第三个靶子。依此类推，每过一关都会新出 现一个靶子，在第 K 关必须一箭射中前 K 关出现的所有 K 个靶子才能进入第 K+1 关，否则游戏 结束。沫沫花了很多时间在这个游戏上，却最多只能玩到第七关“七星连珠”，这让她非常困惑。 于是她设法获得了每一关出现的靶子的位置，想让你告诉她，最多能通过多少关

Input

输入文件第一行是一个正整数N，表示一共有N关。接下来有N行，第i+1行是用空格隔开的三个正整数xi，yi1，yi2 ，表示第i关出现的靶子的横坐标是xi，纵坐标的范围是从yi1到yi2 。
输入保证30%的数据满足N≤100，50%的数据满足N≤5000，100%的数据满足N≤100000且给 出的所有坐标不超过109 。

Output

仅包含一个整数，表示最多的通关数。
Sample Input
5
2 8 12
5 4 5
3 8 10
6 2 3
1 3 7
Sample Output

3

根据题意，对于每个线段我可以列出这样两个方程：
-x*a+y1/x<=b
-x*a+y2/x>=b
然后二分答案以后半平面交判断就行了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define inf 1e100
#define eps 1e-15
#define mid (l+r)/2
const int N=200010;
struct S{double x,y0,y1;}a[N];
struct Point{double x,y;}p[N];
struct Line{
    Point p,v;
    double ang;
    inline void prepare(double k,double b,double kind){
        p=(Point){0.,b};
        double dis=sqrt(1.+k*k);
        v.x=kind/dis;v.y=kind/dis*k;
        ang=atan2(v.y,v.x);
    }
    bool operator < (const Line &x)const{return ang<x.ang;}
}l[N],q[N];
Point operator + (Point x,Point y){return (Point){x.x+y.x,x.y+y.y};}
Point operator - (Point x,Point y){return (Point){x.x-y.x,x.y-y.y};}
Point operator * (Point x,double y){return (Point){x.x*y,x.y*y};}
inline double Cross(Point x,Point y){return x.x*y.y-x.y*y.x;}
inline bool onleft(Line x,Point y){return Cross(x.v,y-x.p)>0.;}
inline Point get_point(Line x,Line y){
    Point u=x.p-y.p;
    double t=Cross(y.v,u)/Cross(x.v,y.v);
    return x.p+x.v*t;
}
inline bool check(int x){
    int h,t,tot=0,i;
    l[++tot].p=(Point){0.,0.},l[tot].v=(Point){1.,0.},l[tot].ang=atan2(0.,1.);
    l[++tot].p=(Point){0.,0.},l[tot].v=(Point){0.,1.},l[tot].ang=atan2(1.,0.);
    l[++tot].p=(Point){0.,inf},l[tot].v=(Point){-1.,0.},l[tot].ang=atan2(0.,-1.);
    l[++tot].p=(Point){-inf,0.},l[tot].v=(Point){0.,-1.},l[tot].ang=atan2(-1.,0.);
    for(i=1;i<=x;++i){
        l[++tot].prepare(-a[i].x,a[i].y0*1.0/a[i].x,1.);
        l[++tot].prepare(-a[i].x,a[i].y1*1.0/a[i].x,-1.);
    }
    sort(l+1,l+tot+1);
    q[h=t=1]=l[1];
    for(i=2;i<=tot;++i){
        while(h<t&&!onleft(l[i],p[t-1])) --t;
        while(h<t&&!onleft(l[i],p[h])) ++h;
        q[++t]=l[i]; 
        if(fabs(Cross(q[t].v,q[t-1].v))<eps){
            --t;
            if(onleft(q[t],l[i].p)) q[t]=l[i];
        }
        if(h<t) p[t-1]=get_point(q[t-1],q[t]);
    }
    while(h<t&&!onleft(q[h],p[t-1])) --t;
    return t-h>1;
}
int main(){
    int i,j,n;
    scanf("%d",&n);
    for(i=1;i<=n;++i){
        scanf("%lf%lf%lf",&a[i].x,&a[i].y0,&a[i].y1);
        a[i].y0-=eps;a[i].y1+=eps;
    }
    int l=0,r=n,ans=0;
    while(l<r){
        if(check(mid)) ans=max(ans,mid),l=mid+1;
        else r=mid;
    }
    printf("%d\n",ans);
}