机器学习 —— 神经网络

最新推荐文章于 2023-07-31 17:28:51 发布

Fancyyj

最新推荐文章于 2023-07-31 17:28:51 发布

阅读量683

点赞数

本文链接：https://blog.csdn.net/Fancyyj/article/details/99715068

版权

一. 神经网络

（一）基础知识

1. 定义

人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。
人工神经网络：是一种应用类似于大脑神经突触联接的结构进行信息处理的数学模型。在工程与学术界也常直接简称为“神经网络”或类神经网络。

2. 神经网络的基本介绍

神经网络起源于1943年，A Logical Calculus of Ideas Immanent in Nervous Activity , 使用一个间划过的计算模型来描述在动物的大脑中，神经元如何通过命题逻辑来实现复杂的计算
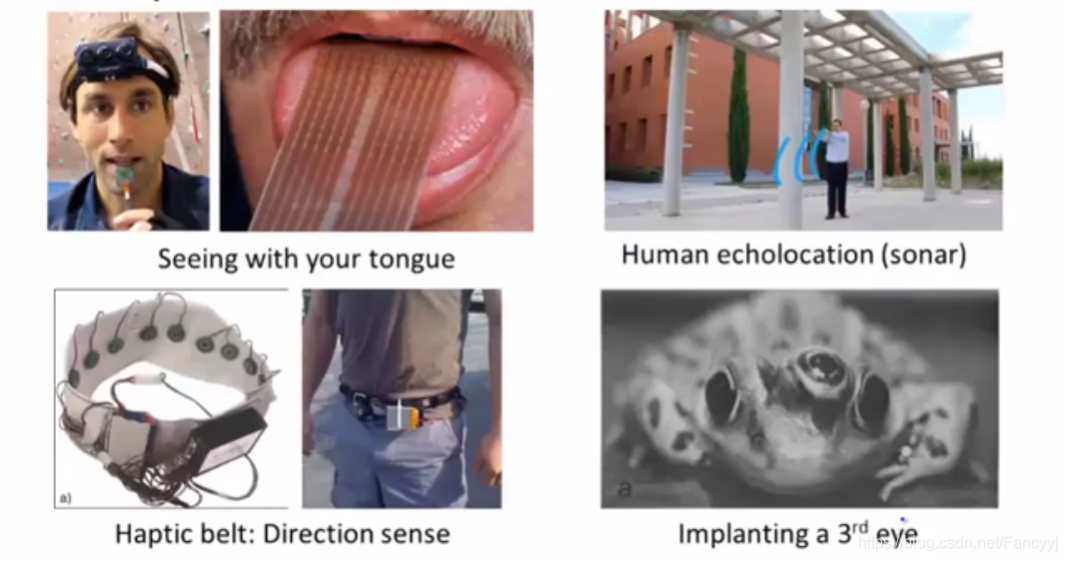
在这里插入图片描述

3.利用神经网络的小发明

在这里插入图片描述

4. 一些基础概念

1）ReLU： Rectified Linear Unit ——修正线性单元
是人工智能常用的激活函数之一
而在神经网络中，线性整流作为神经元的激活函数，定义了该神经元在线性变换wT +b ( T: 转置) 之后的非线性输出结果。换言之，对于进入神经元的来自上一层神经网络的输入向量，使用线性整流激活函数的神经元会输出至下一层神经元或作为整个神经网络的输出（取决现神经元在网络结构中所处位置）。

2） Drop-out正则化
随机失活（dropout）是对具有深度结构的人工神经网络进行优化的方法，在学习过程中通过将隐含层的部分权重或输出随机归零，降低节点间的相互依赖性从而实现神经网络的正则化，降低其结构风险。
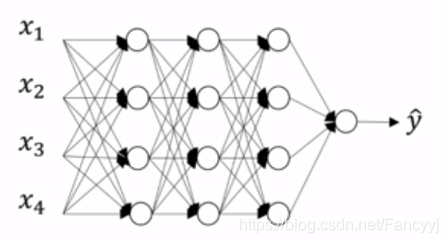
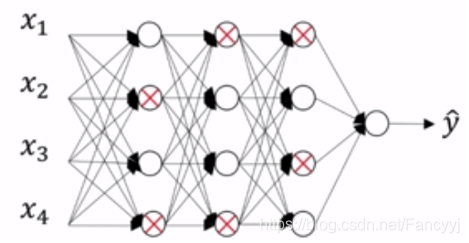
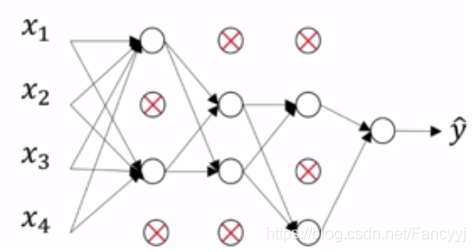
在这里插入图片描述

在这里插入图片描述

3） Inverted DropOut：反向随机失活
3 = np.randm.rand(a3.shape[0], a3.shape[1]) < keep_prob
a3 = np.multiply(a3, d3)
a3 /= keep-prob

假设有50个神经元， keep-prob = 0.8，也就意味着10个左右的神经元要设为0

在这种情况下， z = wa + b 就要减少20%，这样呢，z会越来越小

为了弥补这种情况，我们需要对a进行弥补，弥补的方式就是用a/keep_prob

4）梯度下降的优化算法——指数加权平均
指数加权平均(exponentially weighted averges)也叫指数加权移动平均，通过它可以来计算局部的平均值，来描述数值的变化趋势，
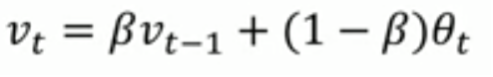
在这里插入图片描述
θ_t：为第 t 天的实际观察值，
V_t: 是要代替 θ_t 的估计值，也就是第 t 天的指数加权平均值，
β：为 V_{t-1} 的权重，是可调节的超参。( 0 < β < 1 )

eg：
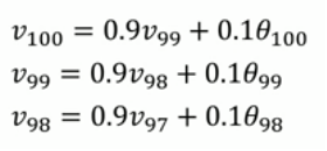
在这里插入图片描述

作用：不同的数据会有不同的权重，这样计算出来的值才更加准确

5）梯度下降优化算法 —— 动量梯度算法
计算梯度的指数加权平均值，并且利用该梯度更新权重值

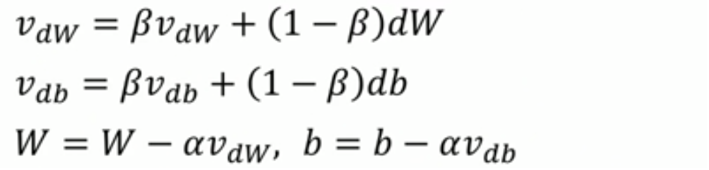
在这里插入图片描述

6） RMSprop
为了进一步优化损失函数在更新中存在摆动幅度存在过大的问题，并且进一步加快函数的收敛速度，RMSProp 算法对权重W和偏置bb的梯度使用了微分平方加权平均数。假设在第t轮迭代过程中：
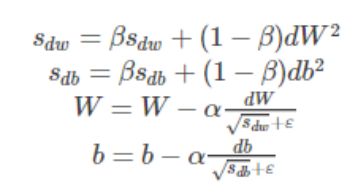
在这里插入图片描述

7）Adam
Adam（Adaptive Moment Estimation）算法是将Momentum算法和RMSProp算法结合起来使用的一种算法
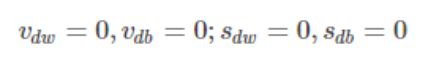
在这里插入图片描述
假设在训练的第 t 轮训练中，我们首先可以计算得到Momentum和RMSProp的参数更新

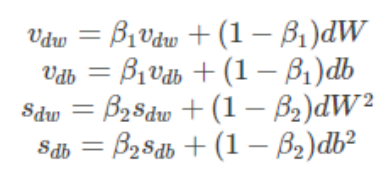
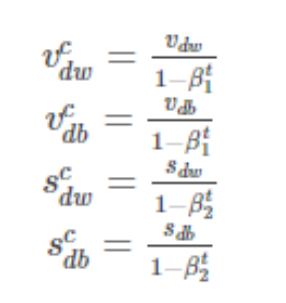
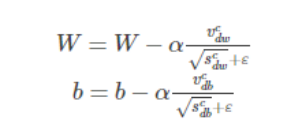
8） softmax函数
softmax函数是对向量进行归一化处理，凸显其中最大的值并抑制远低于最大值的其他分量。
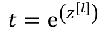
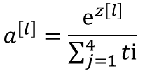
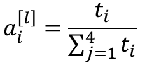
在这里插入图片描述

eg：
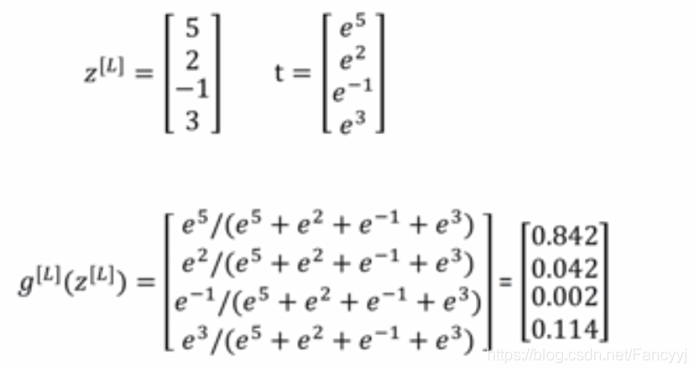
在这里插入图片描述
注：最后算出的结果相加之和是1

（二）神经网络的计算

线性阈值单元： LTU

逻辑回归：
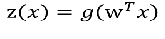
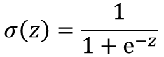
在这里插入图片描述

线性阈值单元LTU（使用阶跃函数代替sigmod函数）
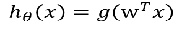
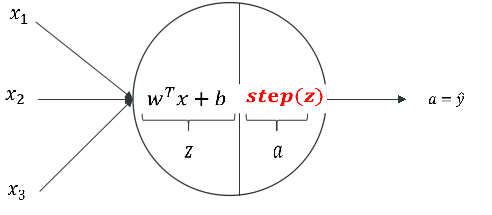
在这里插入图片描述

ps：常用的阶跃函数：

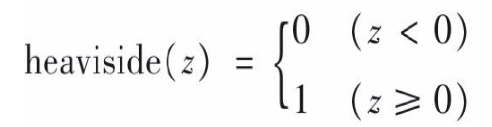
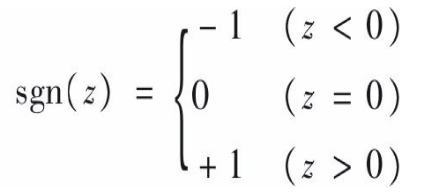
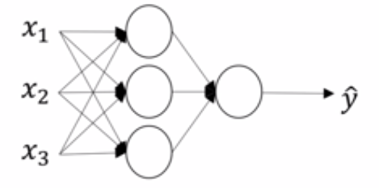
神经网络实际上是多层感知器

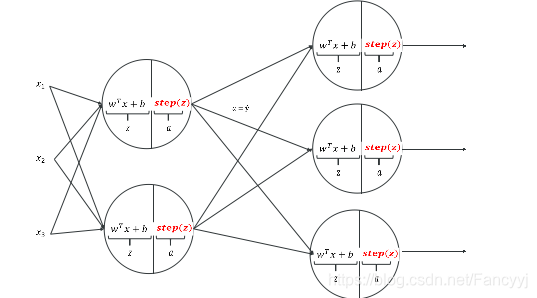
在这里插入图片描述

用符号标识神经网络
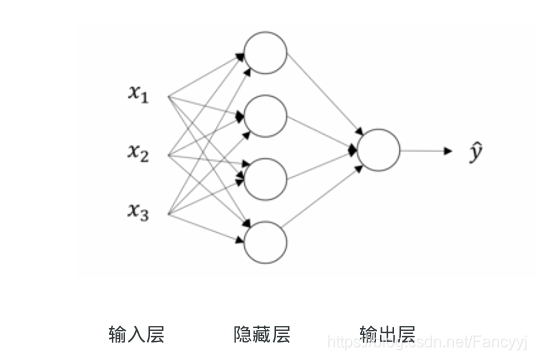
在这里插入图片描述

在训练集当中，我们并不知道这些节点的真正数值
计算层数的时候是不把输入层算在内的，或者可以将输入层定义成第0层。
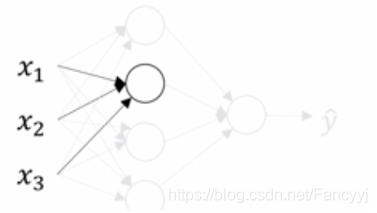
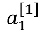在这里插入图片描述表示第一层中的第一个神经元

一个神经元的表达式

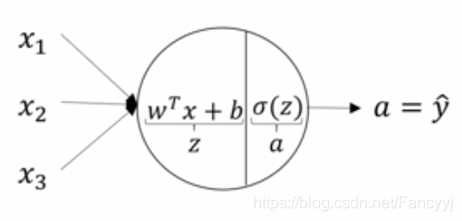
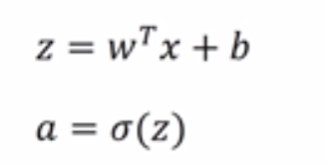在这里插入图片描述
计算顺序：输入计算第一层第一个，计算完第一个再计算第二个，依次类推，层数也一样，计算完第一层再计算第二层直到输出

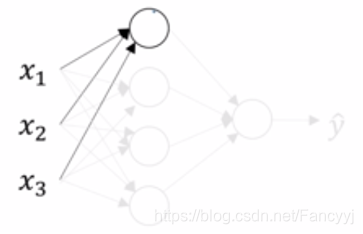
在这里插入图片描述
一层神经网络的数学表达式：

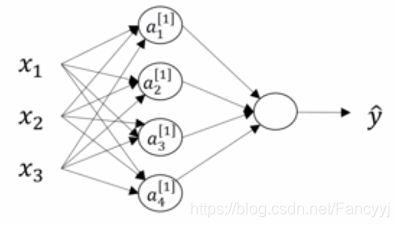
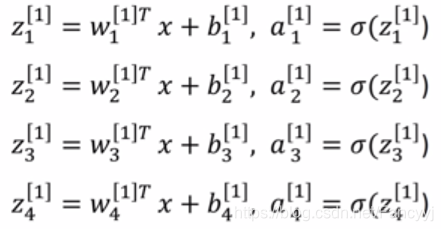
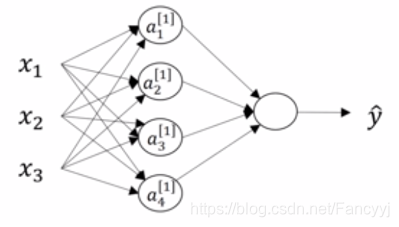
在这里插入图片描述

神经网络的表示

计算完一层神经网络之后，就可以计算整个神经网络：
eg：
在这里插入图片描述
输入：（3， 1）
第一层：WT * X : (4,3)(3,1) = (4,1) sigmoid = (4,1)
第二层：WT * X：(1,4)(4,1) = (1,1) sigmoid = (1,1)
给定了输入值x，计算顺序如下：

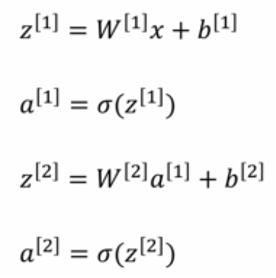
ps： W矩阵的形状：（本层神经元的个数，上一层的输入值数量）

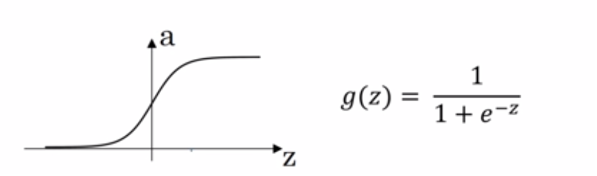
激活函数

激活函数负责将神经元的输入映射到输出端，将非线性的特性引入到神经网络当中。
在这里插入图片描述
给定了输入值x，计算顺序如下：

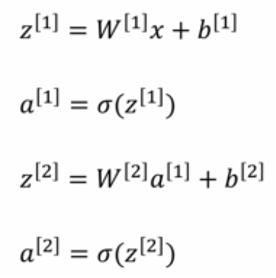
激活函数的作用：

非线性变化
梯度下降
在神经网络发展过程中将激活函数从阶跃函数改成逻辑函数是很大的进步，目的是为了实现梯度下降

非线性激活函数作用：
如果只使用线性激活函数，或者没有激活函数，那么无论神经网络有多少层，计算的都是线性激活函数，因此隐藏层就没有用了

常见激活函数：
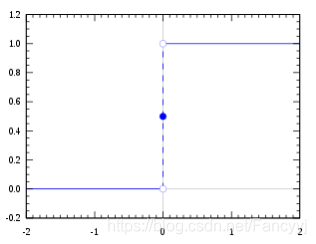
1）Heaviside（Step）阶跃函数
在这里插入图片描述
2）SIgmod函数

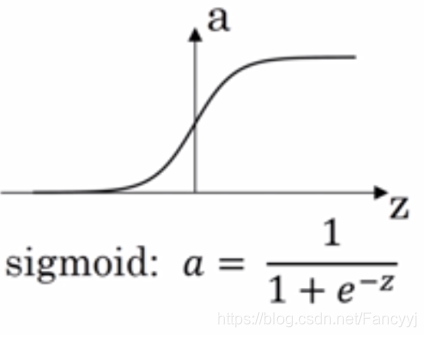
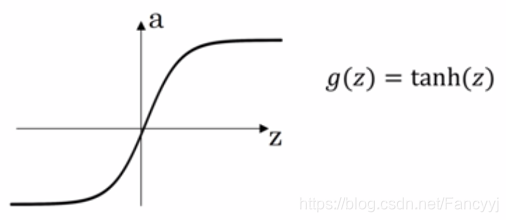
3）tanh函数
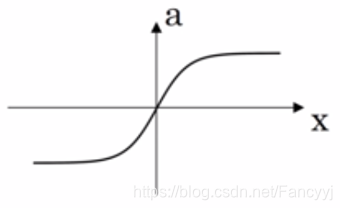
在这里插入图片描述
4）ReLu函数

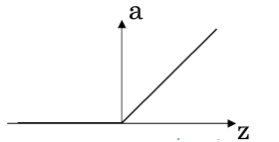
5）Leaky ReLu 函数

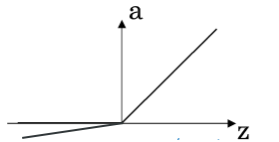
激活函数的导数：
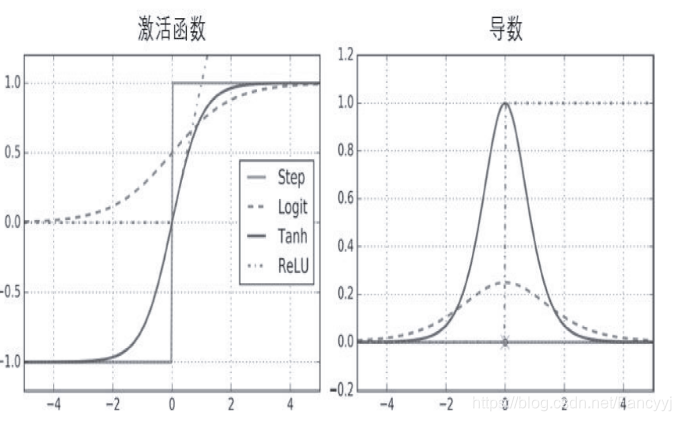
在这里插入图片描述
注：

Step函数的导数一直为0
Tanh输出值是（0,1）
Relu没有最大输出值

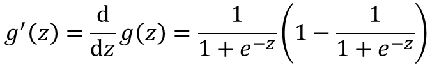
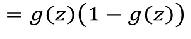
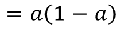
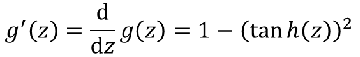
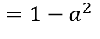
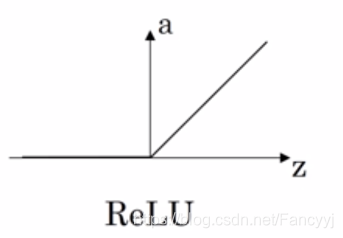
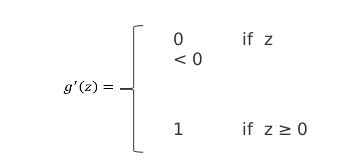
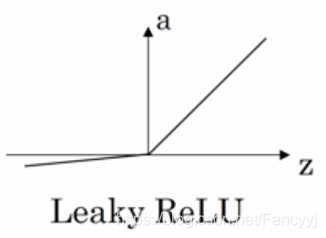
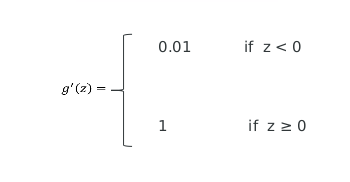
在这里插入图片描述

神经网络传播方向

1）正向传播

对于每一个训练实例，算法将其发送到网络中并且计算每个连续层中的每个神经元的输出
对神经网络逐层进行计算
步骤：
（1）对神经网络第一层计算
1-1 对第一层的第一个进行计算

应用线性函数计算
应用非线性函数进行计算（激活函数： sigmod，Tanh，ReLu，Leaky ReLu）

1-2 对第一层的第二个进行计算
1-3 对第一层的第三个进行计算
…
（2）对神经网络第二层进行计算
…
（3）对神经网络第三层进行计算
…

2）反向传播

通过损失函数（真实值 — 预测值），应用梯度下降，来计算当w[1]， b[1]，w[2]，b[2] 为何值的时候，损失函数最小。
反向传递的过程通过在网络中向后传播误差梯度有效的测量网络中所有连接权重的误差梯度

计算图

计算图被定义为有向图，其中节点对应于数学运算。计算图是表达和评估数学表达式的一种方式。
eg：
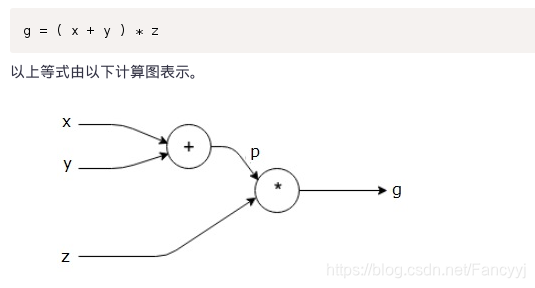
在这里插入图片描述

计算图的导数
导数的意义：通过导数，我们能够直到损失函数的损失来源
eg：
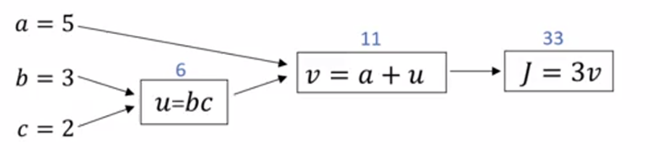
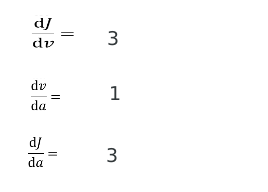
在这里插入图片描述

神经网络的梯度下降

参数：在这里插入图片描述
损失函数：

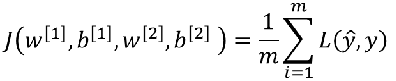
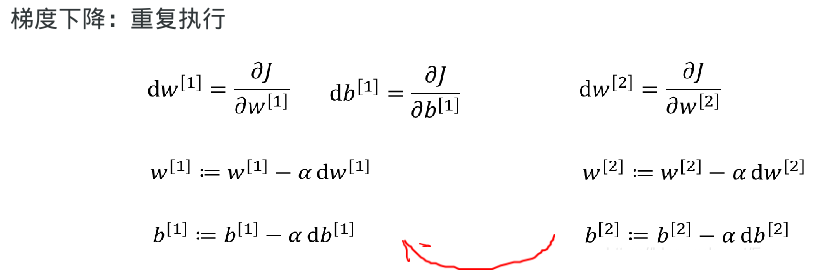
先执行 w[2] 再执行 w[1]

正向传播：
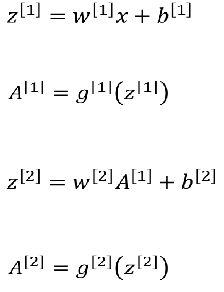
在这里插入图片描述

反向传播：
在这里插入图片描述

神经网络在传播过程中的公式推导：
在这里插入图片描述

神经网络传播过程的公式推导：

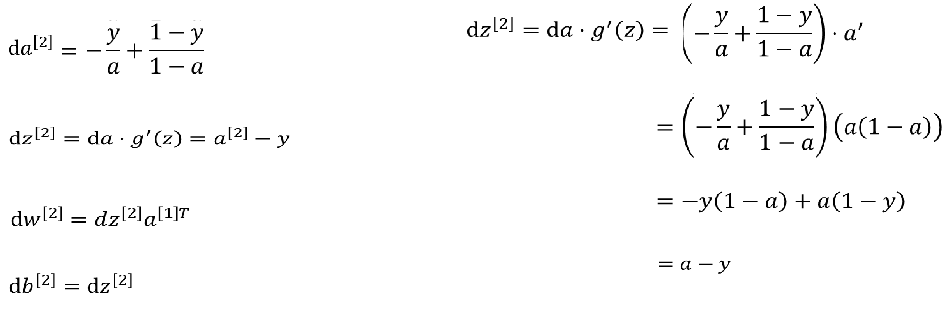在这里插入图片描述）

反向传播的核心：通过导数，得到损失函数的来源，然后减少 / 增大来源，来调试w , b
步骤：
（1）对最后一层进行求导
1-1 我们已知的，不用求损失函数；我们将损失函数求导
1-2 dL / da , a = SIngmod(z)
1-3 dL / dz = ( dL / da ) * (da / dz)
1-4 dL / dw = ( dL / da ) * (da /dz) * (dz/dw)
dL / db = ( dL /da ) * ( da / dz ) * (dz / db)
（2）对倒数第二层进行求导
1-1 dL / w[1] = dL / dz[2] * dz [2] / da[1] * da[1 ]/ dz[1] * dz[1] / dw[1]
1-2 dL / b[1] = dL / dz[2] * dz[2] / da[1] * da[1] / dz[1] * dz[1] / db[1]

…
直到第一层

二. tensorflow 模块

Tensorflow是一种计算图模型，即用图的形式来表示运算过程的一种模型。Tensorflow程序一般分为图的构建和图的执行两个阶段。图的构建阶段也称为图的定义阶段，该过程会在图模型中定义所需的运算，每次运算的的结果以及原始的输入数据都可称为一个节点（operation ，缩写为op）。

（1）查看tensorflow的版本

import tensorflow
print(tensorflow.__version__)

运行结果：
在这里插入图片描述

（2）简单应用tensorflow

variable：是一个变量

import tensorflow as tf

with tf.device('/cpu:0'):
    x = tf.Variable(3, name='x')
y = tf.Variable(4, name='y')
f = x * x * y + y + 2

# 配置一个计算图的上下文环境
# 配置里面是具体运行过程在那里执行给打印出来
sess = tf.Session(config=tf.ConfigProto(log_device_placement=True))
# 碰到sess.run()就会立刻去调用计算
sess.run(x.initializer)
sess.run(y.initializer)
result = sess.run(f)
print(result)
sess.close()

运行结果为：
在这里插入图片描述

（3）图的管理

默认会有一个图，建立一个X1节点，在default 图上，再创建一个x3节点，因为还是默认的default图，那么x1，x3都是默认的default图上。然后新建一个graph图，那么并且在with语句中设置为默认图，此时创建一个x2 节点，那么x2 节点就是在graph图中。with语句结束后，graph图关闭。

import  tensorflow as tf

x1 = tf.Variable(1)
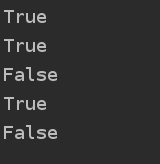
print(x1.graph is tf.get_default_graph())


graph = tf.Graph()
x3 = tf.Variable(3)
with graph.as_default():
    x2 = tf.Variable(2)

x4 = tf.Variable(4)
print(x2.graph is graph)
print(x2.graph is tf.get_default_graph())

print(x3.graph is tf.get_default_graph())
print(x3.graph is graph)

运行结果：
在这里插入图片描述

（4） lifecycle

在tensorflow中，在调用上面的条件的时候不会保存，当时用，当时生成，用完之后就释放了。eg：x = w+3 （w=3）—> x=6； y = x +5 ——> 要先从w的值来得到 x 的值，然后再计算 y 的值

import  tensorflow as tf

w = tf.constant(3)
x = w+2
y = x+5
z= x*3

 with tf.Session() as sess:
     print(y.eval())
     print(z.eval())

print("*********************")
with tf.Session() as sess2:
    y_val , z_val = sess2.run([y,z])
    print(y_val)
    print(z_val)

运行结果为：
在这里插入图片描述
运用了两种方法来解决，其结果都是相同的，差别在于运行的速度和占有的内存。上面的方法是分别建立了两个图，来计算y，z 。这样运行时间较长，并且占用内存，下面的方法是直接将 y 和 z 的放在一起计算出值

（5） autodiff

TensorFlow 提供的autodiff特性可以自动的并有效的为我们计算梯度

实验代码：

import tensorflow as tf
import numpy as np
from sklearn.datasets import  fetch_california_housing
from sklearn.preprocessing import  StandardScaler


n_epochs = 1000
learning_rate = 0.01

housing = fetch_california_housing(data_home='./data',download_if_missing=True)
m ,n = housing.data.shape
housing_data_plus_bias = np.c_[np.ones((m,1)),housing.data]

scaler = StandardScaler().fit(housing_data_plus_bias)
scaled_housing_data_plus_bias = scaler.transform(housing_data_plus_bias)

X = tf.constant(scaled_housing_data_plus_bias,dtype = tf.float32,name = 'X')
y = tf.constant(housing.target.reshape(-1,1),dtype = tf.float32,name='y')

theta = tf.Variable(tf.random_uniform([n+1,1],-1.0,1.0),name = 'theta')
y_pre =  tf.matmul(X,theta,name= 'predictions')
error = y_pre - y
mse = tf.reduce_mean(tf.square(error),name = 'mse')

gradients = tf.gradients(mse,[theta])[0]
training_op = tf.assign(theta,theta-learning_rate*gradients)

init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)

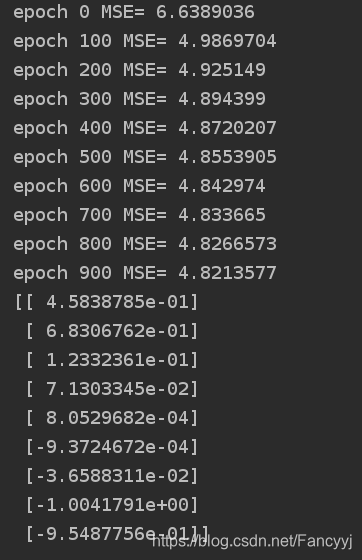
    for epoch in range(n_epochs):
        if epoch %100 ==0 :
            print("epoch",epoch,'MSE=', mse.eval())

        sess.run(training_op)

    best_theta = theta.eval()
    print(best_theta)

运行结果为：
在这里插入图片描述

（6） placeholder

placeholder是一个占位符
TensorFlow中的占位符，用于传入外部数据。
参数：

dtype:数据类型。
shape:数据的维度。默认为None，表示没有限制
name:名称

feed_dict : 是需要传入的值（是一个字典）

import tensorflow as tf

A = tf.placeholder(tf.float32, shape=(None, 3))
B = A + 5

with tf.Session() as  sess:
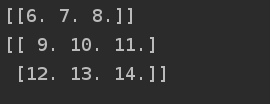
    B_val_1 = B.eval(feed_dict={A: [[1, 2, 3]]})
    B_val_2 = B.eval(feed_dict={A: [[4, 5, 6], [7, 8, 9]]})

print(B_val_1)
print(B_val_2)

运行结果为：
在这里插入图片描述

Fancyyj

关注

0
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
机器学习 —— 神经网络

一. 神经网络（一）基础知识定义人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。人工神经网络：是一种应用类似于...
复制链接

扫一扫