数值优化——牛顿迭代法求解函数零点

一. 问题导入

已知lnx+x^2 =0 在（0,1）范围内有解，用数值方法求解, 精度0.0001

二. 算法原理

首先，f(x) 的值近似于其泰勒展开式：

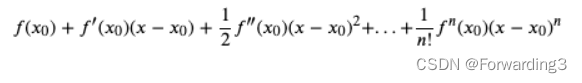
如果只考虑前两项，我们就能得到一个近似等式：
$$f(x)=f(x_0)+f^{{}^{\prime }}(x_0)(x-x_0)$$
代入f(x) = 0，则有：
$$f(x_0)+f^{{}^{\prime }}(x_0)(x-x_0)=0$$
$$x=x_0-\frac{f(x_0)}{f^{{}^{\prime }}(x_0)}$$
故在求函数零点时，有如下迭代公式：
$$x_{i+1}=x_i-\frac{f(x_i)}{f^{{}^{\prime }}(x_{i+1})}$$

C++代码实践

#include <iostream>
#include <vector>
#include <math.h>
using namespace std;

// 已知lnx+x^2 =0 在（0,1）范围内有解，用数值方法求解, 精度0.0001
// 1
// fx = lnx + x^2
// fx’ = (1 / x) + 2 * x
// x(n+1) = x(n) - f(x)/ f(x)'

double newton_Solve(double x) {
	double x0 = x;
	double x1 = x0 - (log(x0) + pow(x0, 2)) / ((1 / x0) + 2 * x0);
	int max_iter = 1000;
	int iter = 0;

	while (iter < max_iter && abs(x0 - x1) > 1e-4) {
		x0 = x1;
		x1 = x0 - (log(x0) + pow(x0, 2)) / ((1 / x0) + 2 * x0);
		iter += 1;
	}
	return x1;
}

int main() {
	double val = newton_Solve(0.5);
	cout.precision(2);   //设置两位有效数字
	cout << val;
	return 0;

}

三. 扩展——求函数的极值点

代入f’(x) = 0，则有：
$$f^{{}^{\prime }}(x_0)+f^{{}^{\prime \prime }}(x_0)(x-x_0)=0$$
$$x=x_0-\frac{f^{{}^{\prime }}(x_0)}{f^{{}^{\prime \prime }}(x_0)}$$
故求函数的极值点时，我们有以下的迭代公式：
$$x_{i+1}=x_i-\frac{f^{{}^{\prime }}(x_i)}{f^{{}^{\prime \prime }}(x_i)}$$