牛顿法入门

介绍

      牛顿迭代法（Newton's method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

     主要是因为多数方程不存在求根公式，因此求精确根非常困难，甚至不可解，从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。

1.应用牛顿法求解方程根

         f(x)在x0处的泰勒级数展开如下：

 这里只展开到一阶导数，即：

令其等于零

化简可得：

但是由于泰勒级数展开只是近似等于原函数，所以这里求解的x1只是近似解，并非原方程真实解，有没有一种方法让近似解的值无限逼近真实值呢？答案是肯定的，我们只需要令x1=x0,继续重复上述步骤，通过迭代就能不断逼近真实解了，即迭代公式为：

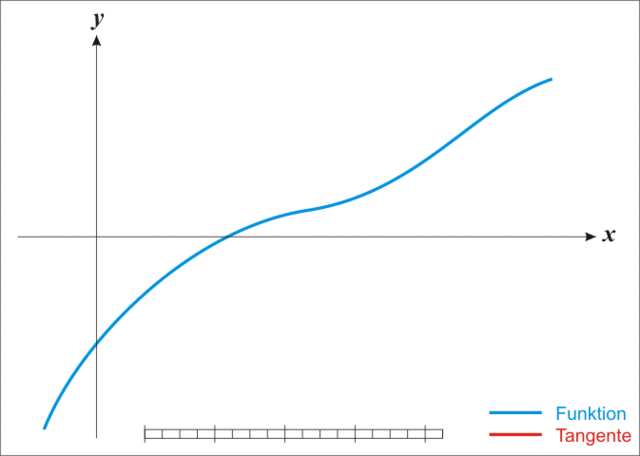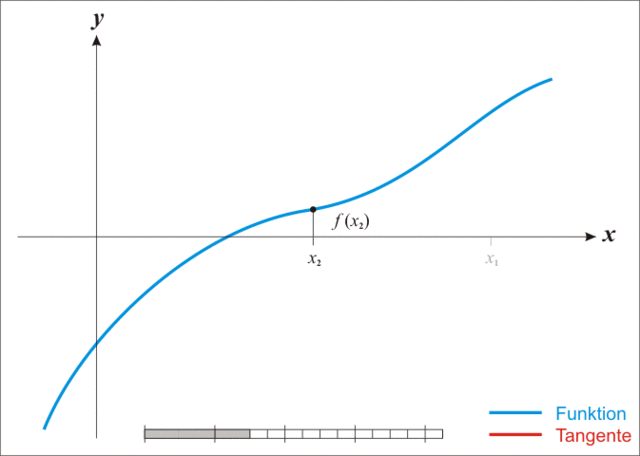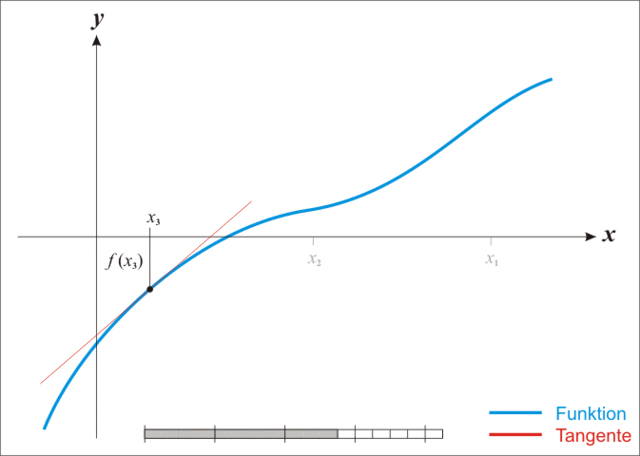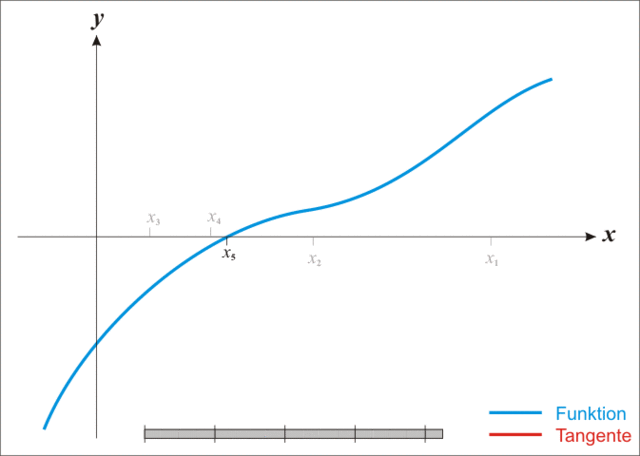
   上图非常生动地展示了迭代求解地过程，可以发现随着迭代次数的增加，近似解不断地逼近真实解，当误差满足我们所需要地精度时，就可以认为二者相等了。

一个简单的求方程根的实例

 这里推荐B站老师讲的一个几分钟地视频：牛顿求根法_哔哩哔哩_bilibili，感兴趣的可以看一下。

matlab求解代码如下：

clc
E = 1E-7;%设置误差精度
C = 3;%这里常数取3
x0 = 5;%设置初值，可以任意值
fun = @(x)x^2-C;%函数表达式
dfun = @(x)2*x;
while true %设置迭代
    x1 = x0-fun(x0)/dfun(x0);
    if abs(x1 - x0) < E
        break;
    end
    x0 = x1;
end
result = x1;

2.牛顿法求解最优化问题

牛顿法也可以应用于最优化问题，是一种被广泛使用并拓展的最优化算法。为了便于理解，我们以一维空间为例：

• 假设 f(x) 是损失函数，我们的目标是找到能够使 f(x) 最小化的 x
• 即对 f'(x) = 0 求解

将牛顿法迭代公式中的 f(x) 替换为 f'(x)，f'(x) 替换为 f''(x)，我们得到新的迭代公式

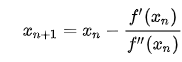
 一元二阶函数最小值实例

 考虑无约束条件，最小值问题

 依据上文求解步骤，matlab代码如下：

clear all;
clc
E = 1E-7;%设置误差精度
dfun = @(x)4*x-16/x^2;%函数一阶导数和二阶导数表达式
ddfun = @(x)4+32/x^3;

x0 = 1;%设置初值，可以任意值
while true %设置迭代
    x1 = x0-dfun(x0)/ddfun(x0);
    if abs(x1 - x0) < E
        break;
    end
    x0 = x1;
end
result = x1;